连续毫米波雷达测速算法研究

张志鹏　刘慧　朱倩倩　陈春阳　陈兵兵

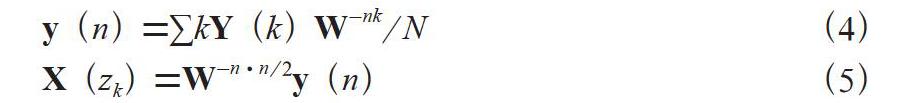
摘  要：首先围绕连续毫米波雷达测速算法展开研究，分析了毫米波雷达的测速原理，引出了其测速本质——谱峰搜索;然后利用快速傅里叶变换这一数字信号处理领域中的经典方法，实现了对雷达回波信号的频谱谱峰位置的快速捕获;为进一步提高连续毫米波雷达的测速精度，在快速傅里叶变换的基础上，再引入Chirp Z变换方法，通过频谱细化实现了对测速算法计算分辨率的有效提升;最后借助MATLAB软件，完成了对所研算法的程序进行编写，并设计了若干算例，通过仿真测试验证了算法的有效性。

关键词：连续毫米波雷达;谱峰搜索;快速傅里叶变换;Chirp Z变换

中图分类号：TN958      文献标识码：A 文章编号：2096-4706（2020）02-0053-03

Abstract：Firstly，the algorithm of continuous millimeter wave radar velocity measurement is studied，the principle of velocity measurement is analyzed，and the essence of velocity measurement—spectrum peak search is brought out. Then，the classical method in the field of digital signal processing，fast Fourier transform，is used to capture the spectrum peak position of radar echo signal. In order to further improve the velocity measurement of continuous millimeter wave radar Accuracy，on the basis of fast Fourier transform，the Chirp Z transform method is introduced，and the resolution of the algorithm is effectively improved through spectrum refinement. Finally，with the help of MATLAB software，the program of the algorithm is completed，and several examples are designed，and the effectiveness of the algorithm is verified by simulation test.

Keywords：continuous millimeter wave radar;spectrum peak search;fast Fourier transform;Chirp Z transform

0  引  言

智能交通系统（ITS）是一种大范围、全方位、实时高效的综合交通运输管理系统，由于其可有效利用现有交通设施，保障交通安全、提高运输效率，正日益受到各国的重视，目前已成为二十一世纪的交通发展方向。在各类现有技术中，雷达[1]凭借其全天候工作的特点，成为ITS系统中监测车流量和车速的最有效的手段之一。其中，目前较有代表性的有美国的Wavetronix雷达、加拿大的RTMS雷達等，它们都属于连续毫米波雷达。本文主要围绕连续毫米波雷达的测速算法展开研究。

1  连续毫米波雷达测速原理

毫米波雷达测速系统主要包括高频头、预处理系统、终端系统和红外启动器等部件，其工作机制为：首先由振荡器产生毫米波（频率f0），经隔离器加至环行器，再由天线定向辐射出去;当电磁波在空间遇到障碍物时发生散射[1]，如目标相对雷达是运动的，则反射回来的电磁波将附加一个与目标运动速度成正比的多普勒频率（fd），使得回波频率变为f0+fd;接收天线收到该回波后，将其经环行器加至混频器，最终在混频器中与本振信号进行混频。

假设目标的径向运动速度为vr，光速为c，则毫米波雷达的本振频率与回波信号中的多普勒频率间存在如下关系：

可见，只要能准确获得fd的值，即可求出目标的运动速度。而fd的信息位于混频器内的中频信号中，其对应的正是中频信号频谱的峰值频率，故能否有效捕获该谱峰频率即成为毫米波雷达测速成功与否的关键。由于当今数字计算机所处理的皆为离散数据，因此必须先对中频信号进行采样，才能进一步借助离散傅里叶变换等数字信号处理[2]工具对其进行频谱分析。

2  快速傅里叶变换及其在谱峰搜索中的应用

众所周知，信号在时、频两个域中具有“周期←→离散”的对应关系[3]，故有限长序列的频谱为一周期且连续信号。对于该类型信号，计算机无法直接进行处理，因此需要对频谱进行采样，从而获得在时、频两个域中皆为周期且离散的信号，进而通过选取主值序列，构造离散傅里叶变换对。而离散傅里叶变换等效于如下的矩阵-向量积运算：

其中X表示离散频谱，W为离散傅里叶变换基，x表示时域离散信号，其计算复杂度颇高，如将其直接应用于中频信号的谱峰搜索，毫米波雷达的测速将彻底丧失实时性，故引入离散傅里叶变换的快速算法——快速傅里叶变换（FFT）。

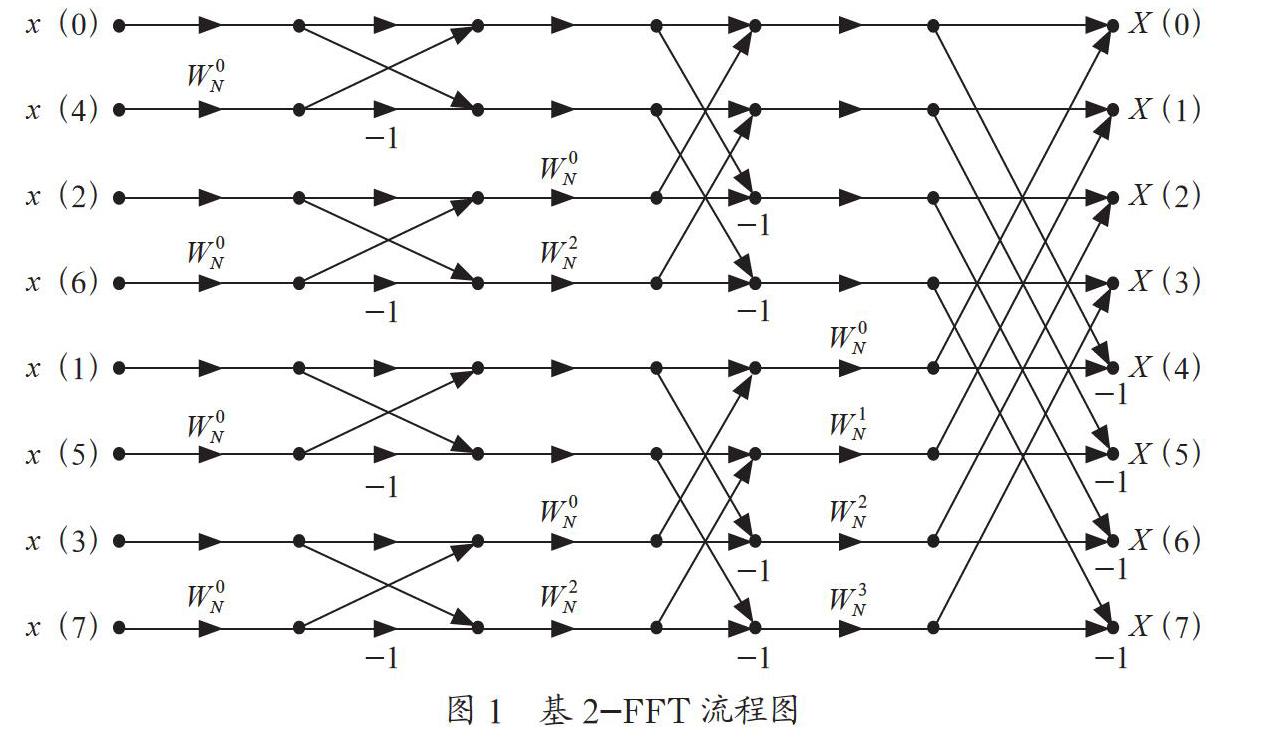
以基2-FFT[2]为例，其算法示意图如图1所示。

基2-FFT利用序列两两分组、层层分级的思想，实现了对序列的离散傅里叶变换的快速求解，其与直接使用式（3）计算相比，时间复杂度降低了2N/log2N倍。因此，使用快速傅里叶变换，可快速获取中频信号的频谱，从而近乎实时地完成对其谱峰所在频段的搜索。

然而，由于FFT的本质是离散傅里叶变换，如果谱线之间相隔较大，则不可避免地会丢失中间的部分重要信息，产生所谓的“栅栏效应”。对于谱峰搜索而言，即意味着峰值频点位置的判定将会出现偏差。因此，在连续毫米波雷达测速系统中，如仅使用快速傅里叶变换对中频信号进行处理，则系统的测量精度势必难以保证。一般而言，为削弱栅栏效应，可通过增加信号的采样点数来缩小谱线间隔，但采样点数的增加将导致计算量也随之大幅增加，这又会使得系统的实时性受到极大影响。

3  Chirp Z变换及其在谱峰搜索中的应用

为弥补离散（快速）傅里叶变换在频谱计算分辨率上的不足，引入Chirp Z变换（CZT）方法[4]，实现对信号频谱的有效细化，从而最终提高连续毫米波雷达的测速精度。

Chirp Z变换主要是利用傅立叶变换和卷积（圆周卷积）的性质，将z平面的单位圆变成一个螺旋线并逐渐地将单位原点移到单位圆内，这样信号的频谱分析即可在z平面的螺旋线上实现（始于任一点，终于另一任意点）。就本质而言，Chirp Z变换并不能减小运算量，但可以计算某个频段的细化频谱，因此是建立在采样点数固定前提下的一种选带细化手段，尤其适用于单一频率信号（对应于毫米波雷达的单目标测速）和频点相距较远的多频率信号（多目标测速），可在FFT锁定谱峰频段后在指定频带内进一步细化搜索峰值频点。

若速傅里叶变换后所选定的频带范围为Y（k），则CZT主要通过以下两个公式进行计算：

其中W表示旋转因子，式（4）的离散傅里叶反变换则可利用图1所示蝶形运算中的FFT算法进行求解。

从算法原理层面看，CZT实现频谱细化的过程如下：

（1）将细化频带转换为z平面单位圆圆周上的一段弧，并确定运动轨迹;

（2）计算给定路径上的CZT;

（3）根据细化频带的频点位置和CZT结果，确定细化频谱。

在实际工程应用中，Chirp Z变换的主要步骤则为：

（1）确定采样频率和对信号的采样点数，连续采样若干段;

（2）选取频谱中的不同频带（就连续毫米波雷达测速系统而言，选带范围即FFT所确定的谱峰周围）;

（3）对每个频带进行CZT细化，直至其中出现单一频率成分，否则进一步增大细化倍数;

（4）在指定频带上寻找谱峰，获得较FFT更精确的频率值、幅值、相位等信息。

本文的算法即是在FFT的基础上，以其粗略频谱作为先验，在指定频带内应用CZT对频谱展开细化，从而在控制运算量的同时，有效提高计算分辨率。

4  仿真实验

借助Matlab平台，对使用发射频率为24.15 GHz、后端A/D采样频率为20.5 kHz的连续毫米波雷达测量速度为1 km/min的单运动目标进行仿真。由式（1）、式（2）可算得，该算例中中频信号的真实谱峰频率应为2683.3 Hz。仿真结果如图2-图4所示。

由上述结果可见，由于存在栅栏效应，直接应用FFT所得频谱的峰值频点为2683 Hz，与真实值存在0.3 Hz的误差;在进一步运用CZT变换后，峰值频点计算结果为2683.27 Hz，精度得到了提高。

值得指出的一点是，CZT所提高的为频谱的计算分辨率，而并非真正意义上的物理分辨率，因此，为进一步提高计算准确性，可适当向后增加采样点数，即可实现更高精度的测速。

5  结  论

本文应用快速傅里叶变换與Chirp Z变换相结合的方法，对连续毫米波雷达后端中频信号的谱峰信息进行提取，从而实现了毫米波雷达系统对运动目标的快速、准确测速。

参考文献：

[1] 许小剑，黄培康.雷达系统及其信息处理 [M].北京：电子工业出版社，2010.

[2] 程佩青.数字信号处理教程：第五版 [M].北京：清华大学出版社，2017.

[3] 郑君里，应启珩，杨为理.信号与系统（下册）：第三版 [M].北京：高等教育出版社，2011.

[4] 马可，张远安，张开生.CZT和ZFFT频谱细化性能分析及FPGA实现 [J].计算机测量与控制，2016，24（2）：288-289+303.

作者简介：张志鹏（1997-），男，汉族，山西晋城人，本科在读，研究方向：雷达信号处理。