网络计划图优化方法研究

郑如炎,张 昆

(海军装备部驻上海地区第一军事代表室，上海 201913)

安排船舶修理作业的计划方法一般包括绘制横道图方法以及网络计划图方法。其中网络计划图法[1]具有直观、可标明关键路线、可进行计算机分析等优点，所以在船舶修理作业中一般采用网络计划图方法安排船舶修理作用计划。随着网络计划方法[2]的发展，对网络计划图的优化逐渐成为修船领域所关注的热点。优化的目的就是通过工期、资源以及费用等网络计划优化，用最小的消耗获得最大的效益。

本文通过实例对网络计划图在工期调整、工期优化、资源优化、工期-费用优化[3]等方面的应用进行说明。

1 工期调整方法

假设以规定工期作为控制标准，可分为2种情况进行讨论。第一种情况是当计算工期短于规定工期时，称网络计划有正时差。这时，可利用时差适当延长持续时间，降低资源消耗强度。第二种情况是当计算工期长于规定工期时，则出现负时差，这时要缩短关键线路上工作的持续时间。若网络计划图中有2条及以上的关键线路，或者调整进度计划重新计算导致关键线路发生了改变，并且计划工期超过了规定的工期，重复使用每次缩短后的持续时间计算新的时间参数，直到计划工期不再超过规定工期或不能调整为止。当计划工期不能满足规定要求时，应该考虑改变网络计划方案，或对网络计划工作的逻辑关系进行调整以缩短计划工期。

2 工期优化方法

工期优化[4]是指压缩网络计划的计算工期满足规定目标，或者在一定约束条件下将工期缩短的过程。在网络计划中，缩短工期可采用以下措施。

2.1 调整工作的组织关系

网络中的组织关系反映了工作中的可变顺序。如图1所示,当工作K和S的施工顺序可以交换时(其中①表示第一道工序，以此类推)，即利用其可变特性将持续时间从原有的20 d缩短到18 d。

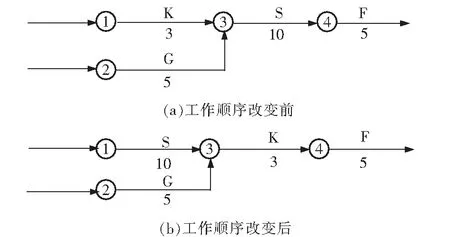
图1 工序调整

2.2 调整逻辑关系

可以根据网络计划的逻辑关系，合理调整网络结构,缩短工期，具体来说包括如下2种方式。

1)将串联作业改成并联作业。初始计划中先进行工作A，后进行工作B。若约束条件允许，可将工作A、B同时进行。这就使得工作时间由原来的10 d缩短到6 d，如图2所示。

图2 串联改变为并联

2)将串联作业改成交叉作业。初始计划中先进行工作A，再进行工作B,最后进行工作C。若约束条件允许，可将作业A、B、C交错进行。这就使得工作时间由原来的70 d缩短到55 d，如图3所示(其中为了区分串联作业工作A、B、C，将并联作业工作对应拆分标记为A1和A2、B1和B2、C1和C2)。

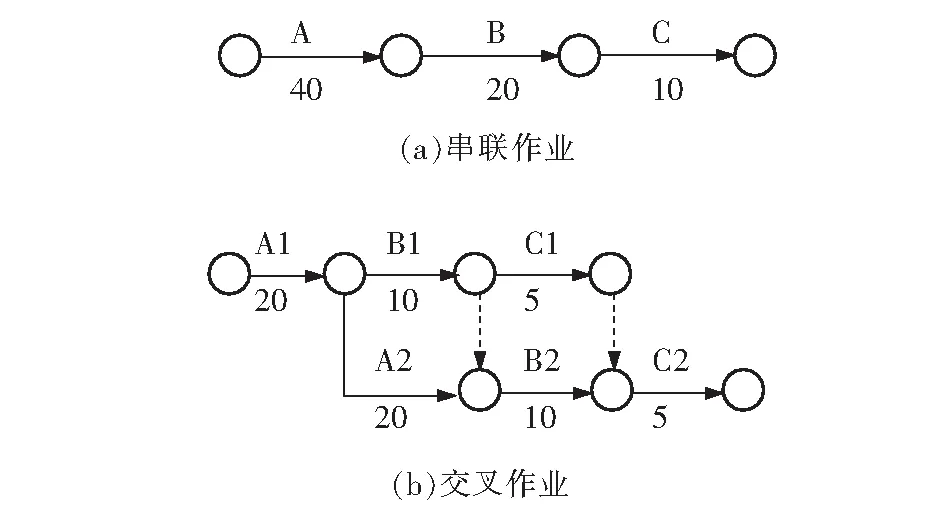
图3 串联作业变更为交叉作业

2.3 压缩关键工作的时间

可以针对关键路径，通过压缩关键工作的持续时间，缩短工期，其主要步骤如下。

1)确定网络计划中的关键线路，并求出计划工期。按要求工期计算相应的缩短时间T:

T=T1-T2，

式中，T1、T2分别表示计算工期和要求工期。

2)按以下因素对缩短关键工作的持续时间进行优先级选择：①对质量安全没有影响或者影响不大的工作；②资源比较充足；③所需成本最低。

3)将优先缩短的关键工作压缩至最短持续时间，再找出关键线路。

4)如计算工期没有满足要求，可重复以上步骤，直到满足要求或者不能再缩短为止。

5)如还是不能达到预期要求，这时可考虑改变原网络计划图的网络结构方法(可参照2.1,2.2措施)。

以某船小修为例，其局部一级网络计划图如图4所示，图4中括号外数字为工作正常持续时间，括号内的数字为工作最短持续时间，其持续时间数据如表1所示。这里我们给出的数据仅仅作为参考，以便探讨说明工期优化的步骤。其中假设要求工期为5 d。

图4 局部一级网络计划图

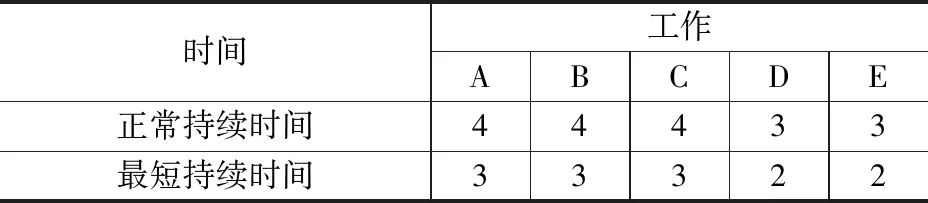
表1 某船小修持续时间 d

1)求出在正常持续时间下的计算工期为7 d。

2)计算工期应该缩短的时间为2 d。

3)因为工作A、B、C正常与最短持续时间都相等，工作D、E也是一样，所以先选择关键工作A、B、C进行缩短。

4)将关键工作A、B、C缩短至最短持续时间3 d，计算工期为6 d，缩短时间为1 d。

5)由于计算工期还是比要求工期大，需继续压缩，即考虑将关键工作D、E进行压缩。

6)将关键工作D、E缩短至最短持续时间2 d，计算工期为5 d，满足要求工期，调整后的网络计划如图5所示。

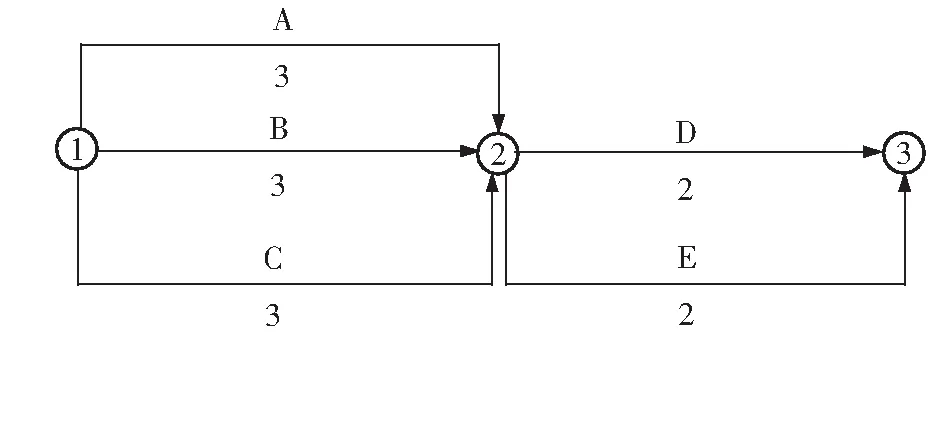
图5 调整后的网络计划图

2.4 调整资源，缩短关键路线

利用时差，从非关键线路上进行挖掘，将某些资源调到关键线路上，从而增加人力和物力，进而缩短关键线路上的持续时间。

如图4所示，如果工作A、B、C以及工作D、E的正常持续时间不同,即存在着关键工作与非关键工作。这里假设工作A、D为关键工作，当将工作A进行压缩后可能会变成非关键工作，这时需将其松弛，使之继续成为关键工作，其松弛时间介于正常持续时间与最短持续时间之间。

3 资源优化方法

调整工期仅仅涉及到时间的安排，并没有将计划实现所应具备的物资条件考虑进去。而若工作进度安排不当，就会产生某些工作的资源供需矛盾。这就要求应该最大限度的降低成本，进而取得更好的经济利益。资源优化可分为以下两类问题。

3.1 资源有限，工期延长最短

解决工作资源冲突的步骤如下。

1)检查网络计划中工作是否存在资源冲突。

2)在冲突段，调整工作使用资源的使用顺序，其应遵循工期增加最小的原则，直到满足资源限制为止。

3)调整网络计划，重新计算工作时间参数。

4)将资源成本增加量与工期成本增加量进行比较分析，得到优选方案。

3.2 工期规定，资源均衡

将资源优先分配给关键工序和总时差较小的工序，并利用时差，错开时间，合理统筹协调，进而达到资源均衡、持续地被加以使用。衡量物资资源需求量均衡程度的指标有：极差、方差以及均衡系数。不同的指标对应不同的优选方案，我们应当合理选择方案，达到最优效率。本文主要讨论削峰法，其主要步骤如下。

1)计算网络计划的各个时间参数，绘制以最早开始时间为起点的网络计划图。

2)找出资源需求最大时间段及其最大资源强度，确定目标最大强度值。

3)进行比对调整，对于最大资源强度超过目标最大强度值的时间段，对该时间段中的所有工作，主要针对非关键工作中的最早完成时间最短者以及最迟开始时间最长者进行统计：当最早完成的时间最小值等于最迟开始时间最大值，则对比调整结束；当最早完成的时间最小值小于最迟开始时间最大值，则应考虑将最迟开始时间最大值的工作开工时间调整为最早完成的时间最小值。

4)重复上述步骤，直至对比调整结束。

本文主要讨论第二种规定工期的资源均衡问题，即给出一个关于某船的部分小修工程网络计划图的简单例子来说明削峰法的步骤。其初步网络计划图见图6，持续时间数据见表2，假设工期为122 d，其在工作进行50 d时，C、F工作共用1台大型机器，而该机器仅能支持一项工作，而C工序仅在前期23 d使用该机器。

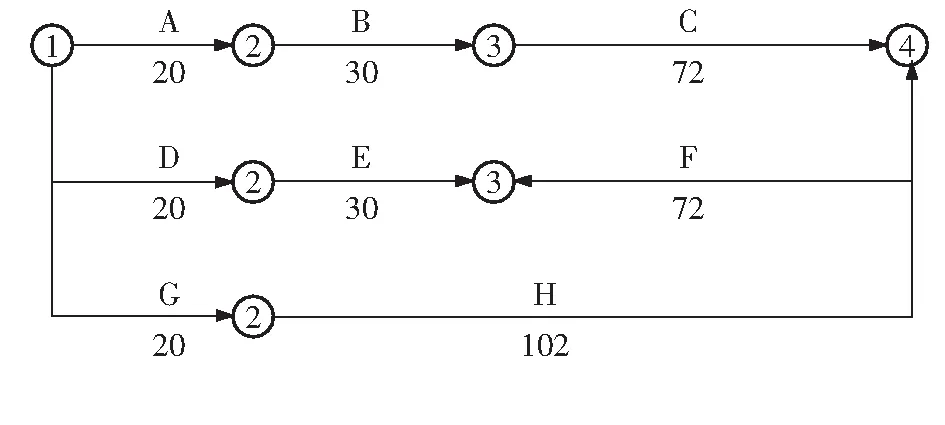
图6 初步网络计划图

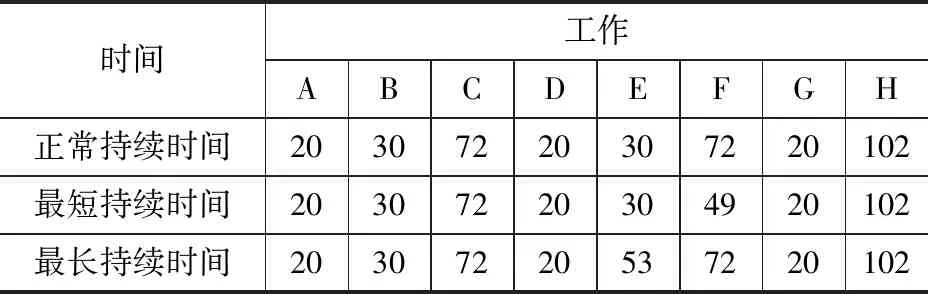
表2 利用削峰法计算的某船小修持续时间表 d

1)由表2、图6知，其关键工序为A-B-C工作。

2)确定资源需求最大的时间段为50～73 d,最大资源强度为2台机器，目标最大强度值为1台机器。

3)最大资源强度超过目标最大强度，即考虑将工作F适当推迟以避开工作C、F同时工作的资源冲突。

4)最大资源强度等于目标最大强度，即对比调整结束，其调整后网络计划图如图7所示。

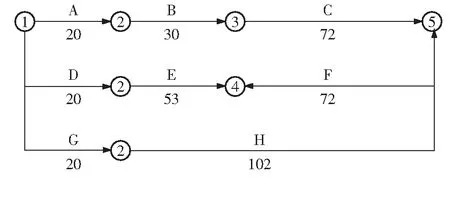
图7 调整后网络计划图

4 工期-费用优化方法

制定网络计划不仅要考虑工期、资源情况，还要考虑费用。工期-费用的优化[5]就是根据其相互的关系，对网络计划的时间与所需成本同时进行调整，以寻求最佳经济效益，即寻求费用最少的最优工期。工程项目的成本主要包括直接费用和间接费用两部分。在费用与工期的关系中，一般有最优工期，或者总费用较低的合理工期，而总费用与直接费用、间接费用的关系曲线则如图8所示。

图8 费用关系图

工期-费用优化步骤为：①从工作的持续时间和费用关系中找出使计划工期缩短，间接费用增加最少的工作，缩短其持续时间。②考虑间接费用随着工期缩短而减小的影响，利用工期变化引起直接费用、间接费用变化之和，求出总费用最小所对应的工期或规定工期对应的最小总费用。

工期-费用优化可采用的方法为渐进算法，即网络计划中的工作采用正常持续时间和成本，以关键工作的持续时间和费用关系为依据，将缩短关键工作持续时间的可能性和非关键工作时差之间的制约关系加以综合考虑，进而不断调整网络计划，得到一系列计算工期与总费用之间的关系和工作的进度安排。

5 结束语

网络计划图编制的科学性与规范性是舰船修期控制的必要保证。通过网络技术的优化，可以形成工期短、质量好、成本低以及资源利用率高的计划方案。随着大型网络的发展，手工优化已逐步向计算机自动化优化发展，本文为大型网络计划的优化提供思路与方法，进而可能在修船领域带来可观的经济效益。