基于改进SLP 方法的铁路物流中心布局规划研究
叶玉玲,刘佳林,梁恒达,贾咏明
(1. 同济大学道路与交通工程教育部重点实验室,上海201804;2. 上汽大众汽车有限公司,上海201805;3. 上汽通用汽车销售有限公司,上海201210)
铁路货运站是铁路货物运输的基本场所,但目前很多货运站依旧保持传统状态,功能设施陈旧,原始布局不够科学,制约了铁路货运的发展。 铁路物流中心是依托铁路枢纽和大型铁路货运场站建立起来的,为客户提供以铁路运输为主的全方位、一体化现代物流服务的空间场所,它是集物流、商流、信息流和资金流于一体的综合节点[1]。 合理地规划和建设铁路物流中心,对于全面提升铁路全程物流服务能力,调整铁路货场的功能定位和布局,促进铁路规模化、集约化发展具有重要意义。
国外对物流中心的研究远早于我国,且随着国外学者对工厂设施布局问题研究的深入,方法模型呈现多态化,取得了越来越多的研究成果。普遍认为设施平面布局问题属于NP-hard 问题,因此无法简单地通过传统函数单调性求解。 大多数学者将物流中心布局问题归为优化问题,而根据问题的表述方式,可分为离散和连续布局问题。 总的来说,用来解决物流中心布局问题的模型大致可以分为二次分配模型、混合整数规划模型、多目标规划模型等。 当布局为离散且规划区域被分为若干个面积相等的区块,每个区块放置一个设施,布局问题可用QAP 模型来表示[2];当将布局问题看成是连续问题时,可用混合整数规划模型来表示[3];当布局优化目标为两个及以上,布局问题就变成了多目标规划问题[4]。对于设施布局问题,可采用精确算法、启发式算法及其它算法求解。 由于设施布局问题的复杂性,采用精确算法需要花费大量的时间,而启发式算法能在最短时间内生成可行解,各学者主要采用启发式算法来解决设施布局问题,包括遗传算法、禁忌搜索算法、模拟退火算法、蚁群算法以及它们的组合算法等。 对于铁路物流中心平面布局问题,国外几乎没有相关文献,而国内学者对其有一定研究,布局的方法大致分为系统布置规划法(SLP)方法[1,5]、改进的SLP 方法[6-7]以及其他方法。
综上,目前对于铁路货运中心的布局问题国内外研究较少,国外基本没有针对铁路物流园区功能区布局的相关研究,多是关于设施布局方面的讨论。而国内相关研究多是基于SLP 方法建立数学模型,没有充分考虑到铁路物流中心特点,缺少一定的理论支撑,没有一套科学完整的布局方法。 因为铁路物流中心是依附于铁路货运枢纽的货物集散中心,其货物品类、作业流程等和一般物流中心有一定差别。 因此,铁路物流中心布局问题是一种特殊的物流中心布局问题,需要结合铁路自身特征和铁路货运发展需求来考虑其平面布局规划。
1 铁路现代物流中心功能分析
在进行铁路现代物流中心功能区布局设计时,不仅要满足物流中心的各项功能需求,还要达到铁路货运与现代物流一体化,优化内部物流作业流线和周围交通设施。根据铁路物流中心的整体定位、客户物流需求及物流中心内部业务流程特征,可将物流功能区分为以下三类。
1) 基本物流功能区。 主要包括集装箱功能区、长大笨重货物功能区、散堆装货物功能区、包裹快运货物功能区、商品汽车功能区和危险货物功能区。
2) 延伸物流功能区。主要包括流通加工区、多式联运区和仓储配送区。流通加工区办理货物的分类、分割、组装、刷标志、贴标签等流通加工作业;多式联运区办理货运在铁路物流中心与其它交通方式的衔接作业;仓储配送区办理货物的存储和在装车发货前的拣选、分装业务。
3) 配套功能区。配套功能区主要包括办公事务区、停车场区、综合服务区。办公事务区主要提供员工进行业务工作所必需的办公场所;停车场区为铁路物流中心内部运输装卸车辆、外部配送车辆以及员工车辆提供停车场所;综合服务区为铁路物流中心员工提供餐饮、活动交流所需要的场所。
2 基于改进SLP 方法的铁路现代物流中心功能区布局方法
SLP 方法是一种将物流分析与功能区之间关系密切程度分析相结合以求得合理布局的技术,在布置设计领域得到了广泛的应用,相对于一般数学模型法,其对影响因素的考虑更加全面,并将影响因素定量化。但传统SLP 方法存在人为主观因素较大、缺乏对交通因素及作业流线的考虑等问题;因此,部分学者[6-7]在原始SLP 方法的基础上,将其得出的综合相关系数作为重要参数建立多目标模型,对SLP 方法进行改进。本文在改进SLP 方法的基础上,运用AHP 模糊综合评价法对最优布局解集的方案进行评价,得到最终的功能区布局方案。 具体步骤如图1 所示。
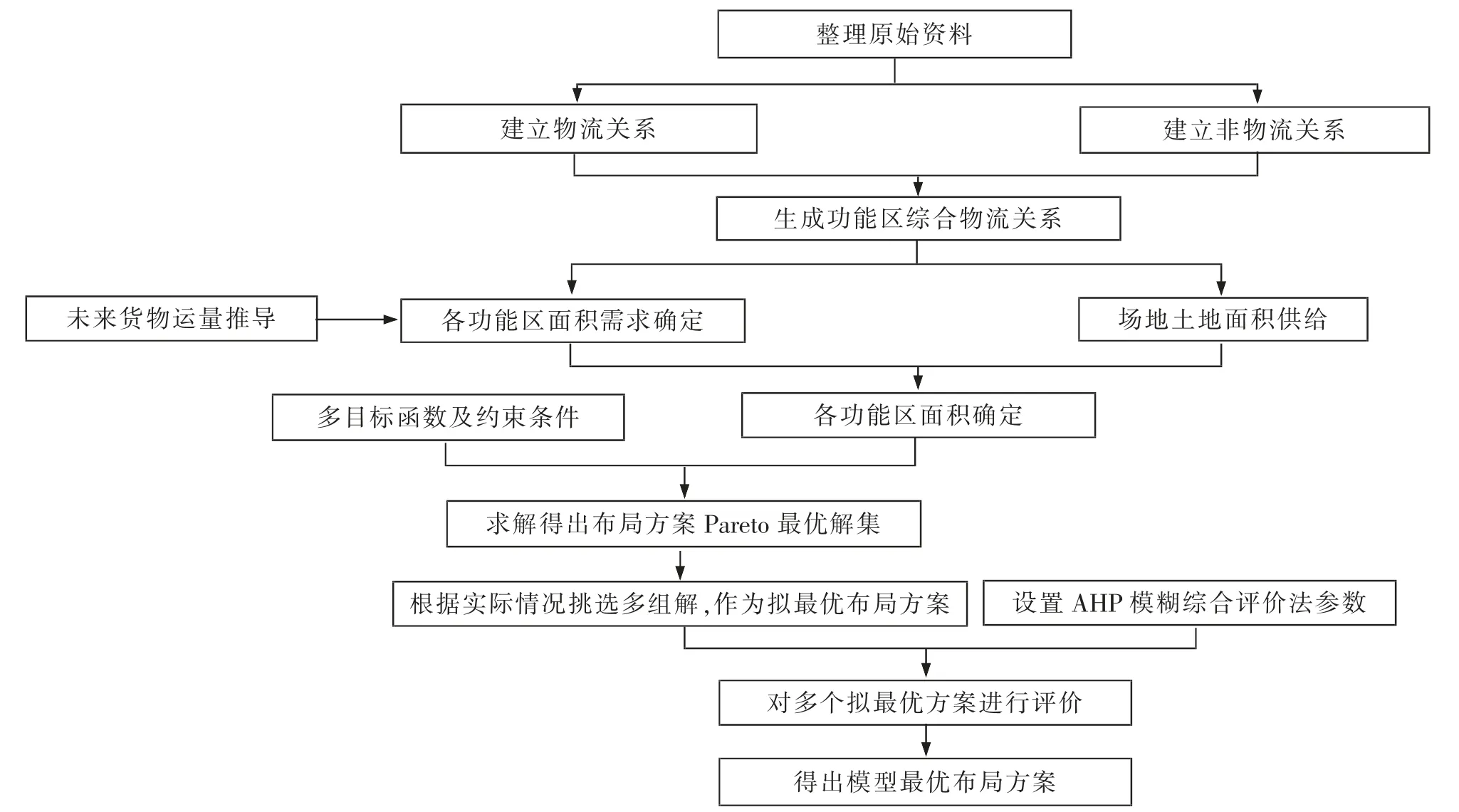
图1 改进的SLP 方法实施步骤框架Fig.1 Improved SLP implementation step framework
2.1 构建模型
2.1.1 假设条件
①假设铁路物流中心各个功能区均在同一个二维平面上;
②假设待规划的铁路现代物流中心功能区的个数为n, 以铁路物流中心所在平面的左下角为坐标原点,向右为X 轴正方向,向上为Y 轴正方向;
③假设各功能区的几何外观均为矩形,且各边都与二维布局坐标的X 轴和Y 轴平行;
④假设物流中心外部既有交通设施、 铁路线路或其它区域作为布局模型中的固定区域,不会因功能区优化布置而发生位置调整;
⑤假设(xi,yi)和(xj,yj)分别为功能区i 和功能区j 的中心点坐标。
模型示意图如图2 所示。
2.1.2 目标函数
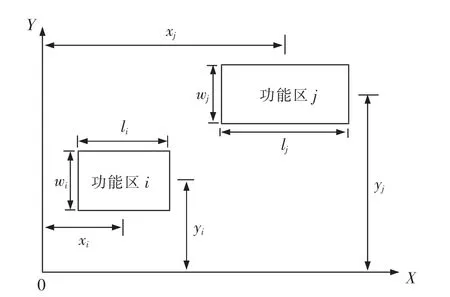
图2 坐标示意图Fig.2 Schematic diagram of coordinates
根据提高铁路现代物流中心整体运输效率、降低运输成本的总布局原则,以功能区之间相关关系最大和总体搬运成本最小为目标,分别建立函数模型。 具体如下

式中:Z1表示各功能区相关关系的总和;Tij表示功能区i 和功能区j 之间的综合相关关系值;bij表示功能区i和功能区j 之间的邻接程度,可由功能区之间的曼哈顿距离dij转化而来,dij=|xi-xj|+|yi-yj|,具体由表1 可知;Z2表示各功能区整体搬运成本的总和;cij表示功能区i 和功能区j 之间的单位搬运成本;qij表示功能区i 和功能区j 之间的日平均物流量。
另外,为了使模型可以表达出功能区可行的横倒和竖立两种放置样式, 设fi为0-1 变量,表示功能区的放置形式

可以看出,功能区横倒和竖立对应其长宽值的互换。
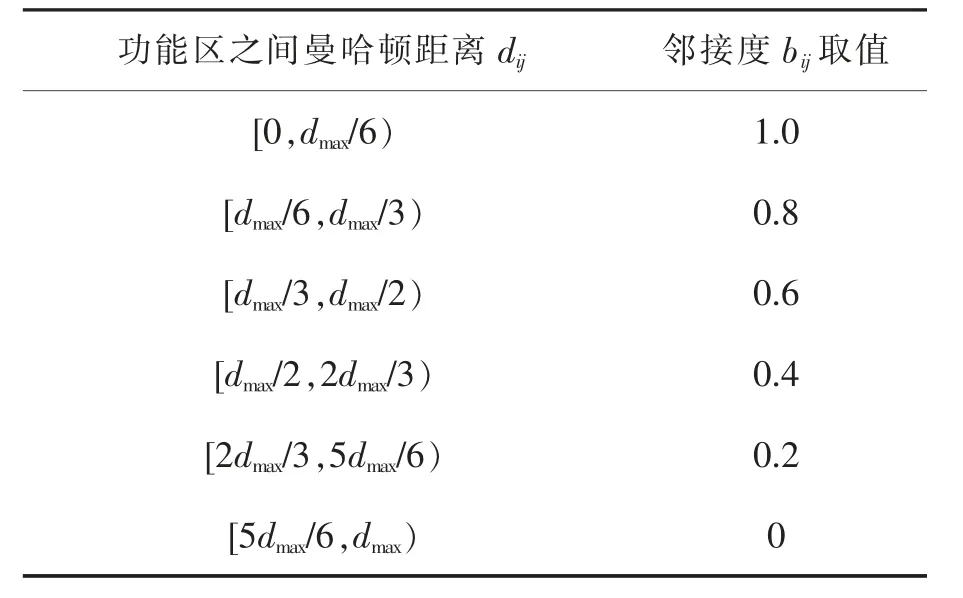
表1 功能区邻接度量化表Tab.1 Quantification of functional area adjacency degree
2.1.3 约束条件
本文设置了以下7 个方面的约束,以此来保证模型的合理性和科学性。
①功能区不重叠约束。 在铁路物流中心布局时,应保证各功能区两两之间相互不重叠。其中,li和wi分别表示功能区i 的长度和宽度,pij表示相邻功能区i,j 之间的最小距离。
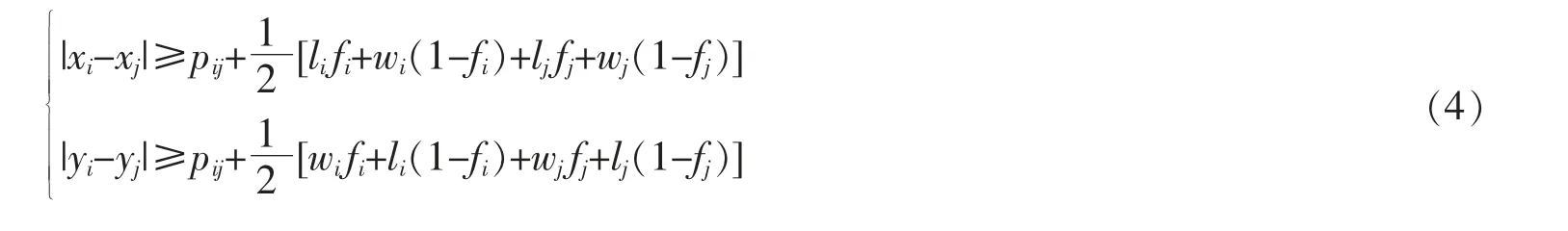
②边界约束。 在铁路物流中心布局时,应保证各功能区在整体布局范围内。 其中:mi表示功能区i 与其相邻的规划区域边界的最小距离;L,W 分别表示铁路物流中心规划区域的长度和宽度。
③功能区总面积约束。 所有功能区面积的总和不能大于铁路物流中心的整体规划面积,S 表示铁路物流中心规划区域的占地面积。

④固定约束。由于假设了外部既有线路、设备不会因功能区的布置而发生位置改变,因此在功能区布局时应对功能区的可行位置进行固定约束,以防止把功能区设置在这些区域。 用Fk表示物流中心的固定区域,则
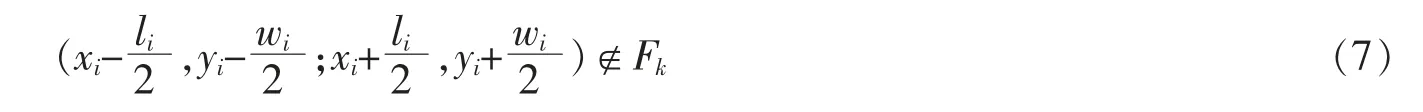
⑤物流中心出入口约束。 在铁路物流中心布局时,应保证铁路物流中心的出入口在整体布局范围边界上,以确保货物能正常地进出铁路物流中心。

⑥交通流线规划约束。为避免产生交通流线重叠、冲突等结果。需以以下方式进行约束:设货物k 的作业流程序列sk是由D 集合的功能区所组成,即sk=(sik,sjk,…,spk),其中,i,j,p∈D,sik表示功能区i 是货物k的一项作业流程;设|i-j|k表示功能区i 和功能区j 在货物k 的流程序列sk内的顺序距离,如序列sk=(sak,sbk,sck)中,|a-b|k≤|a-c|k。 因此,当满足以下不等式时,可对货物k 的交通流线的交叉现象加以一定程度的约束。其中,m∈D,tijk表示货物k 功能区i 到功能区j 之间移动的次数。 式(9)和式(10)可抽象表述为:功能区在货物流线序列中的距离越近,则实际地理位置也应越近。

⑦功能簇团约束。 考虑将各功能作业区在位置布局相互隔离、相互划分出来,以避免不同作业之间的业务交叉。设人员动线序列qh由H 集合的功能区所组成,即qh=(qeh,qrh,…,qth),其中e,r,t∈H,qeh表示功能区e 是人员流动过程h 的一项作业流程;设||qh||表示人员动线序列qh的长度,则序列qh的功能区加权地理坐标(xh,yh)为:xh=(xe+xr+…+xt)/||qh||,yh=(xe+xr+…+xt)/||qh||,e,r,t∈H。 同理可得货物作业流程序列sg的加权地理坐标(xg,yg)。 由此,则功能簇团约束为

2.2 模型求解
由于本文建立了一个多目标模型,常规求解方法分为直接方法和间接方法。间接方法将多目标问题转化为单目标问题,进而降低了求解的难度,但往往照顾不到所有的子目标函数性能,在转化的过程中造成一定的失真。 多目标遗传算法是一种广泛被用于求解多目标问题的仿生算法,NSGA-Ⅱ(第二代非劣分层遗传算法)具有收敛能力高、运行时间少以及解分布较好等优点。 本文运用该算法进行模型求解,步骤如下:
1) 编码。 采用序列编码和二进制编码相结合的编码方法。 用正整数{1,2,3,4,…,n}来表示物流中心功能区的编号,用{0,1}二进制编码来表示功能区的放置方向。 染色体可表示为Ri={f1,f2,f3,…,fn|θ1,θ2,θ3,…,θn},其中fn表示第n 个功能区的编号,θn表示第n 个功能区的放置方向。
2) 初始化种群。 当先验知识不充分时,可以随机初始化群种个体,以此获得第一代个体;当先验知识充分时,可把先验知识作为初始化第一代种群个体的边界来加以约束。
3) 确定适应度函数。 直接将目标函数作为适应度函数,即:Fit(Z1)=Z1,Fit(Z2)=-Z2。
4) 非支配排序。 计算个体解的适应度函数, 找出全部非支配个体解, 得到种群的第一级非支配层(Rank),然后删除这些个体,对种群重复以上操作,得到所有个体的分层等级。
5) 快速非支配排序。 当种群代数大于等于2 时,找到种群中所有的Pareto 最优个体,将其存放于集合F1;将F1作为第一层非支配个体的集合并赋予统一参数;找到F1中每个个体的支配个体集S,并在S 中找到所有的Pareto 最优个体,将其存放于F2;重复以上操作,直到所有个体均被分级。
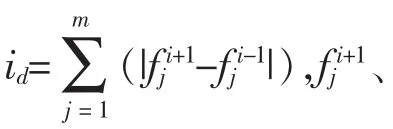
7) 选择、交叉、变异。 采用二进制锦标赛选择法对种群进行选择。 对于符号编码,进行部分匹配交叉操作,并采用逆转变异;对于二进制编码,进行双点交叉,并采用基本位变异。
8) 精英策略。 将父代和子代的所有个体混合后再进行非支配排序,以持久化父代的优秀基因编码。
2.3 方案评价
由于多目标求解得出一个最优解集,故需要对方案集进行评价,选出最终的布局方案。 本文采用AHP模糊综合评价法进行评价,用AHP 法得到权重矩阵,再结合模糊综合评价法进行最终评价。
当采用AHP 层次分析法得到权重向量W 和评价矩阵R 后,可按下式计算综合评价结果

其中,bj为评价对象对评语集等级的隶属度。 最后,根据隶属度最大的原则来确定布局方案的优劣等级。
考虑到多目标遗传算法最优解可能不止一个,需对最终多层次、多因素的评价结果进行汇总,因此还需对B 进行集约处理。 本文基于兼顾各因素的影响效用,采用评价集对应的分数向量S 来对综合评价矩阵B进行处理,以得到系统总得分F

式中:S=(s1,s2,…,sk)T。
3 案例分析
3.1 基本参数确定
S 市计划在原有铁路货场上建立铁路物流中心,项目建设面积为52.5 万m2,中间有河道横穿物流中心,如图3 所示。
参考《铁路货运中心设计暂行规定》、《铁路车站及枢纽设计规范》以及国家建筑用地规范,结合对该物流中心2025 年的货运量预测,得到各个功能区的需求面积(见表2)。编号11及12 所代表的货物出入口、 货物和人员出入口在实际中是固定的, 坐标位置分别为(700,370)和(330,0)。 此外,河道横穿物流中心,其面积约为35 000 m2。
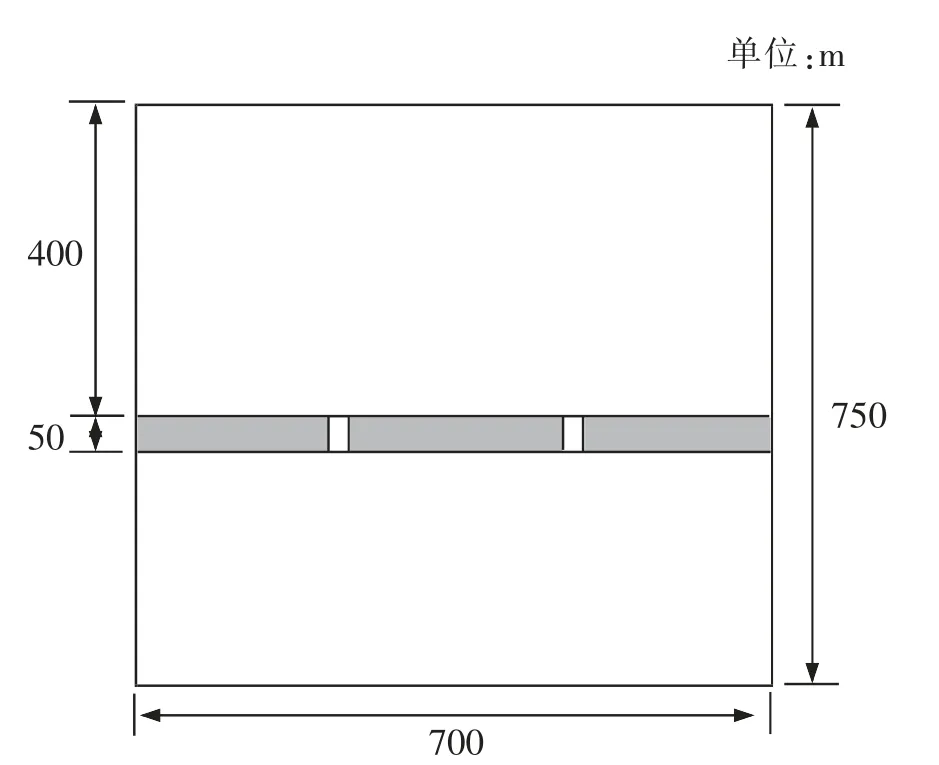
图3 S 市西站平面基本范围图(阴影部分:河道)Fig.3 Basic plane scope map of S west railway station(shaded part: river)
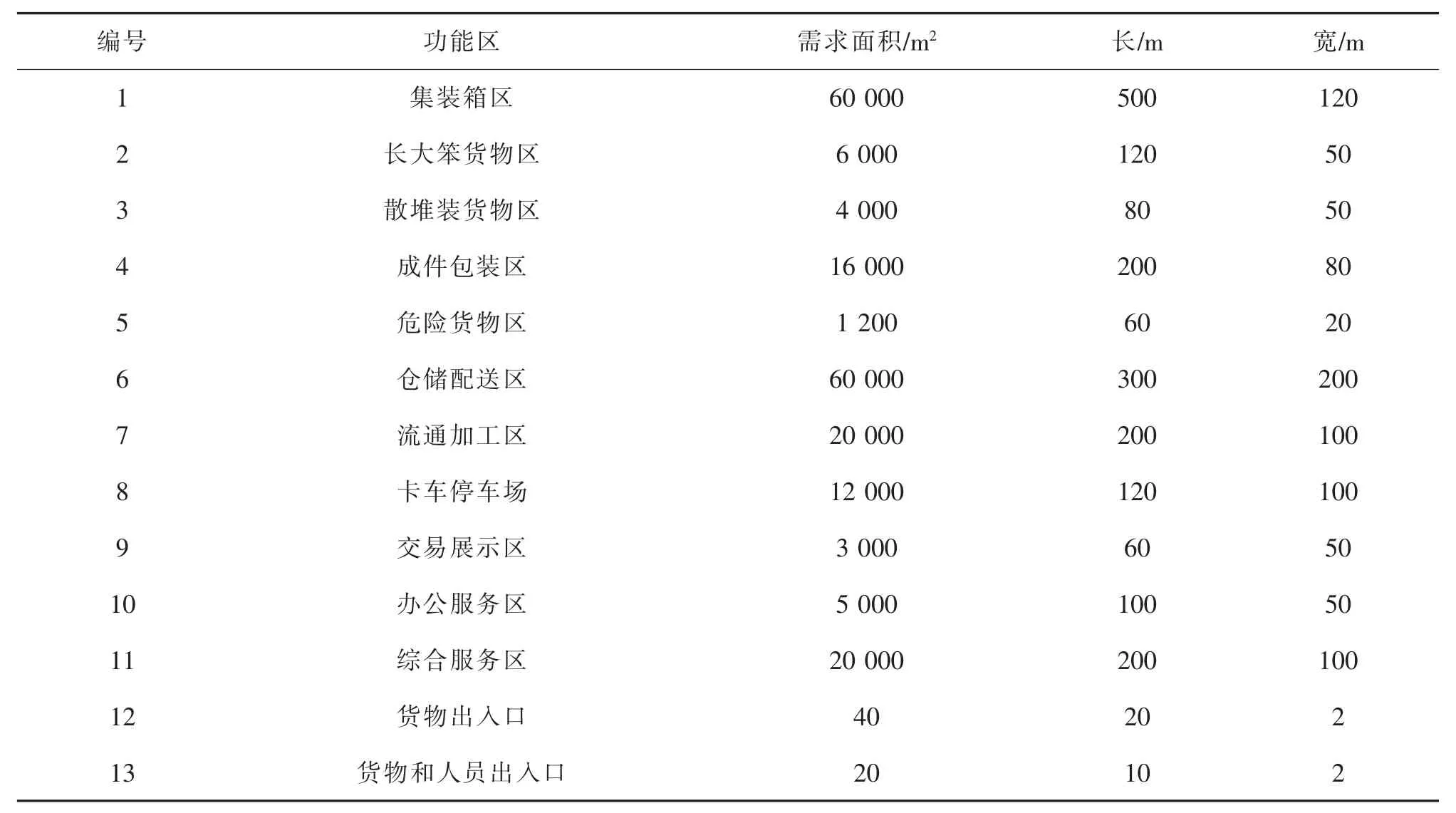
表2 铁路物流中心各功能区需求面积Tab.2 Required area of each functional area of railway logistics center
依据预测的铁路物流中心物流量和货物作业流程,结合实际调研数据,并参考相关研究成果[6],可得铁路物流中心各功能区的日均物流量pij和单位距离搬运成本cij,如表3 和表4 所示。此外,根据铁路物流中心道路规划的相关规定,结合各功能区之间的物流强度,对功能区最小间距进行设置,见表5。
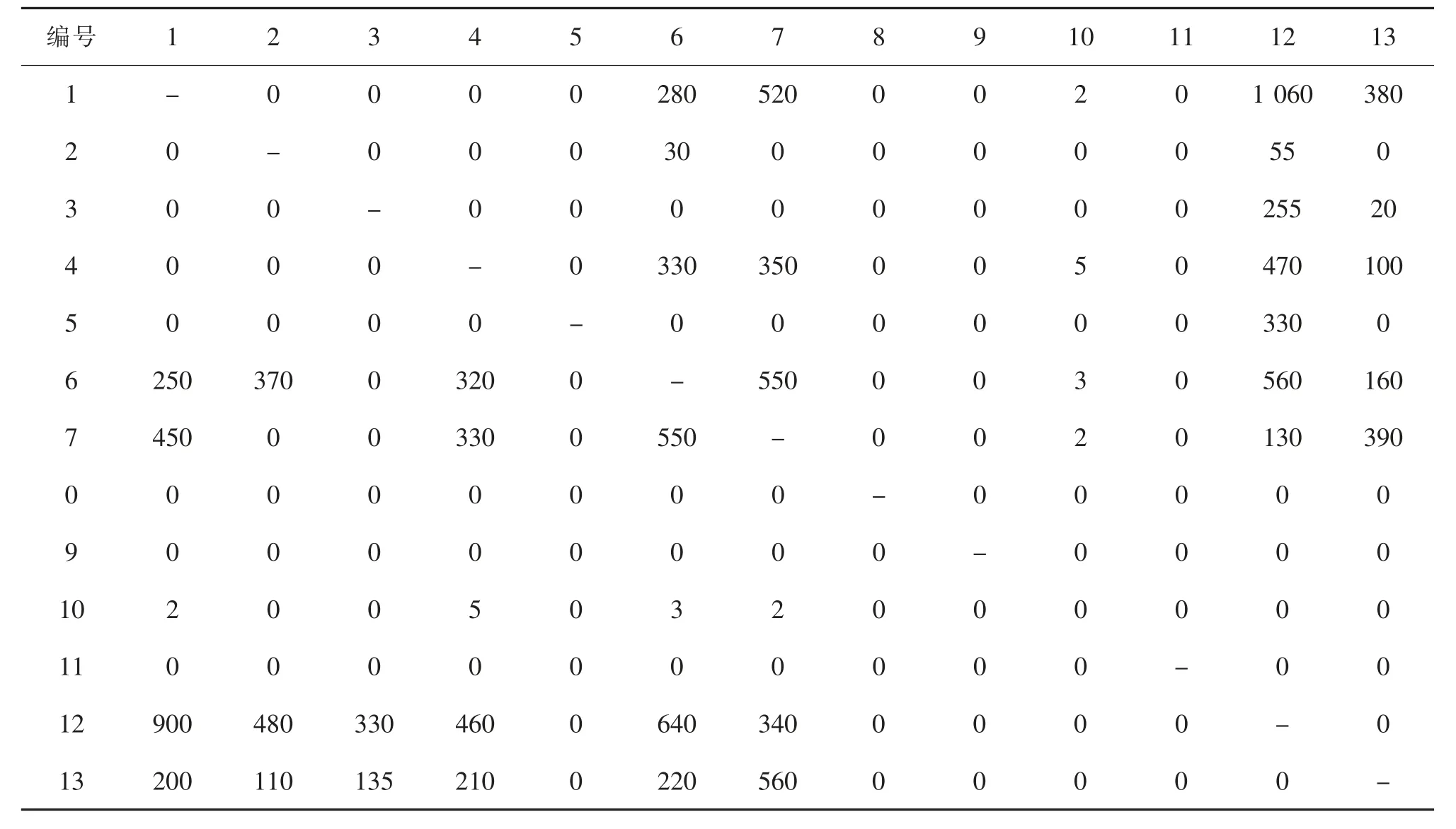
表3 S 市西站物流中心功能区间的日均物流量Tab.3 Average daily material flow between function areas of logistics center of S west railway station t
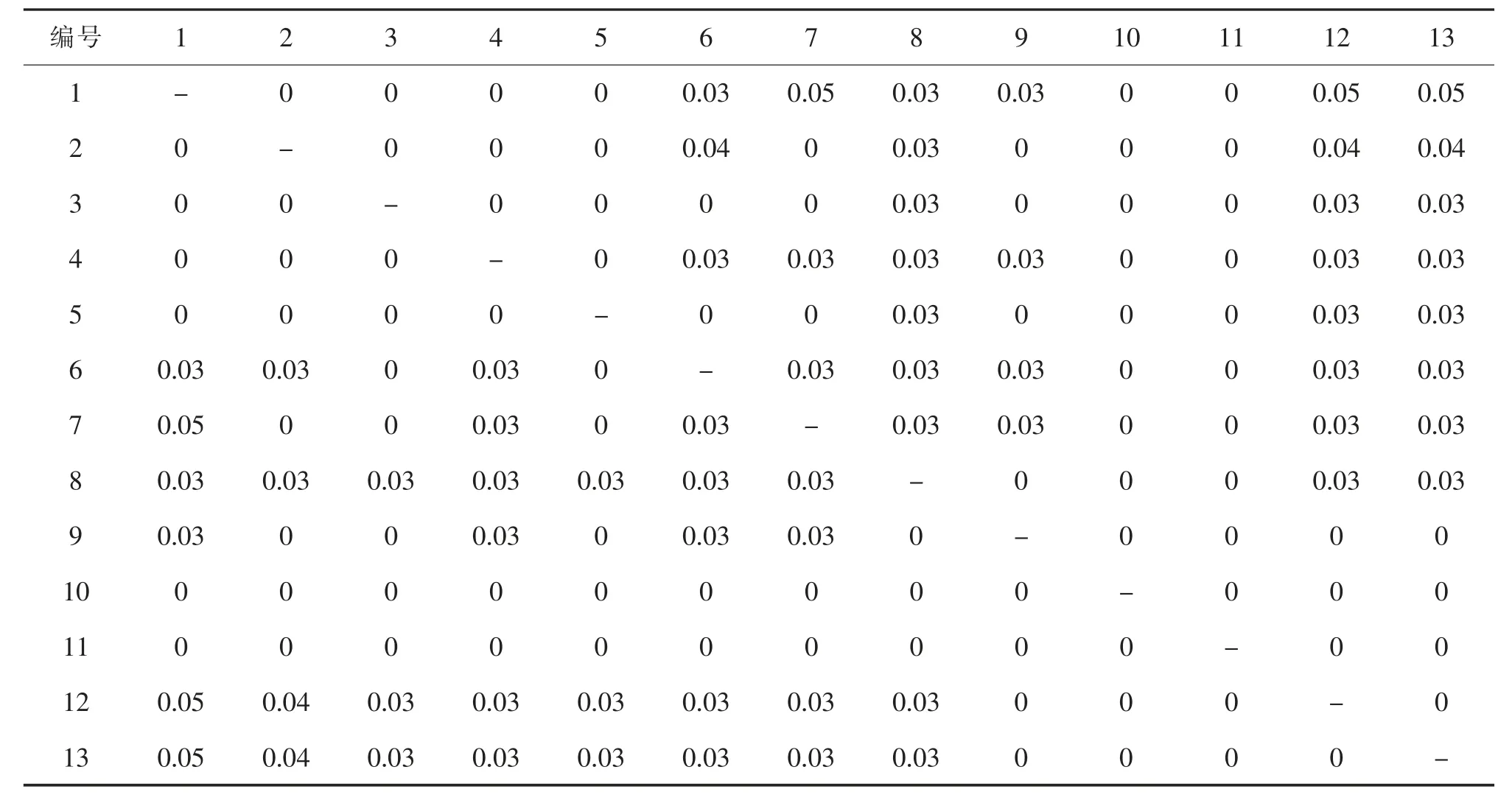
表4 S 市西站物流中心功能区间的单位距离搬运成本Tab.4 Unit distance handling cost between functional areas of logistics center of S west railway station 元/km
物流相关关系等级与非物流相关关系等级划分存在一定差别,在统一分析之前,需要通过加权的方式使两套等级划分规则具备可比性。将综合相关关系划分为6 个离散等级,用符号A,E,I,O,U,X 分别表示关系密切程度为“绝对必要靠近”,“特别必要靠近”,“重要”,“一般”,“不重要”和“不可靠近”。假设物流与非物流相关关系同等重要,即加权系数m∶n=1∶1。加权后综合相关关系取值范围为-1~8,并有A:7~8,E:5~6,I:3~4,O:1~2,U:0,X:小于0。 由此得到各功能区之间的综合相关关系见表6。
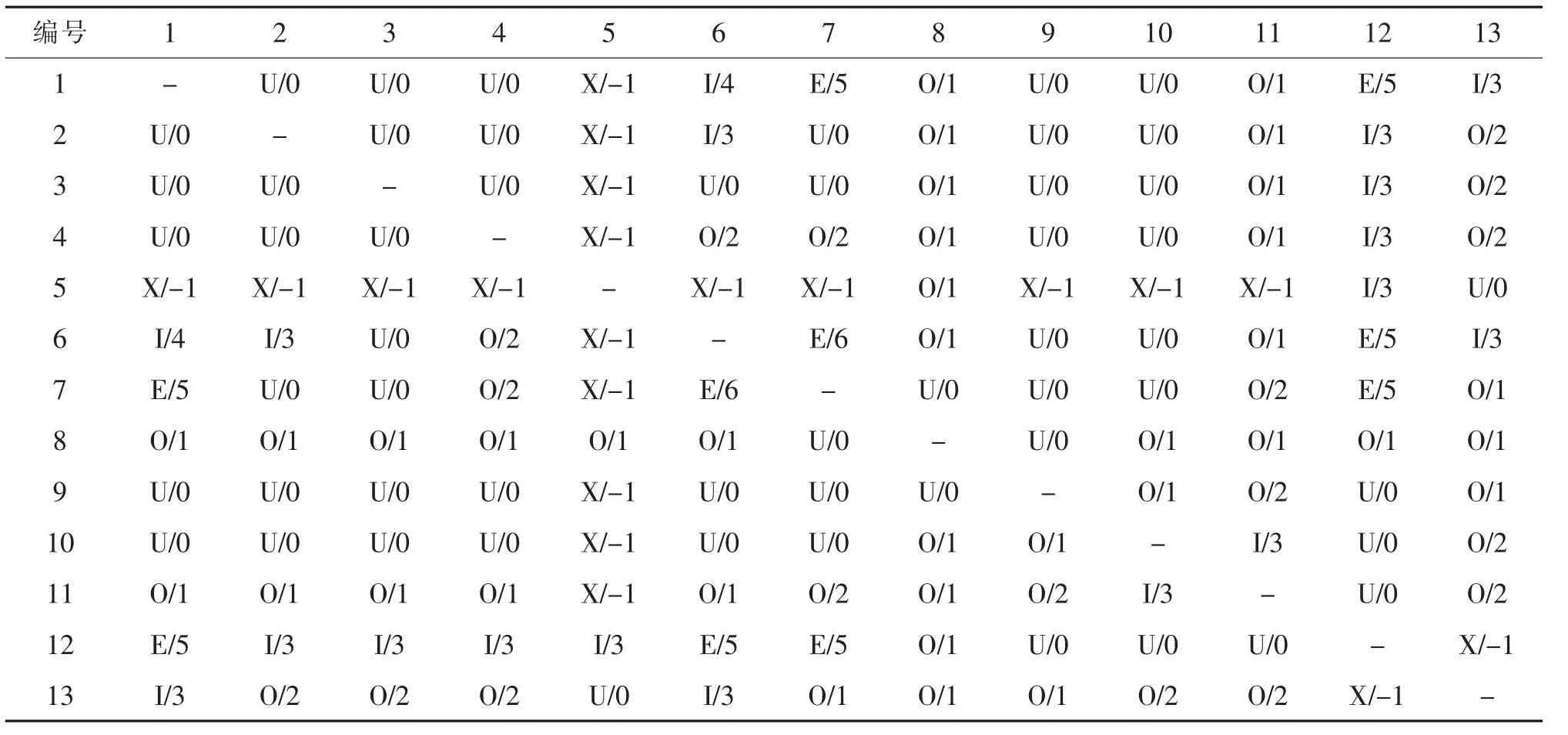
表6 综合相关关系表Tab.6 Comprehensive correlation
3.2 布局模型求解
根据NSGA-Ⅱ遗传算法的一般参数设置原则,本文对其进行如下指定:种群容量psize=1 000,交叉概率pcross=0.95,变异概率pmutation=0.02,遗传代数Gmax=1 000。
利用Python 编写遗传算法程序,反复运行20 次直至结果稳定。由于多目标问题最终得到包括不止一个解的Pareto 最优集。 因此,我们在结合实际的情况下从该解集中选出相关系数Z1最大且总搬运成本上升幅度最小的对应解R1*,以及总搬运成本Z2最小且相关系数上升幅度最大对应的解R2*,染色体组合如下所示:
R1*={1,5,2,3,7,4,12,8,6,13,10,11,9|1,1,1,1,1,1,1,1,0,1,0,1,0}
R2*={1,5,2,4,3,7,12,8,11,6,13,9,10|1,1,1,1,1,1,1,1,1,0,1,0,1}
对两染色体表达进行功能区坐标映射推导,得到布局结果如图4 和图5 所示。

注:1 为集装箱区;2 为长大笨货物区;3 为散堆装货物区;4 为成件包装区;5 为危险货物区;6 为仓储配送区;7 为流通加工区;8 为卡车停车场;9 为交流展示区;10 为办公服务区;11 为综合服务区;12 为货物出入口;13 为货物和人员出入口。
最后,根据AHP 方法得出指标权重为W=(0.075 2,0.219 6,0.130 3,0.044 8,0.07,0.210 1,0.056 4,0.022 4,0.035 5,0.045 2,0.090 4)。 另外,对专家问卷调查中对拟最优布局方案的评价进行汇总处理,得到二级指标的模糊隶属度数据,即评价矩阵R,如表7 和表8 所示。
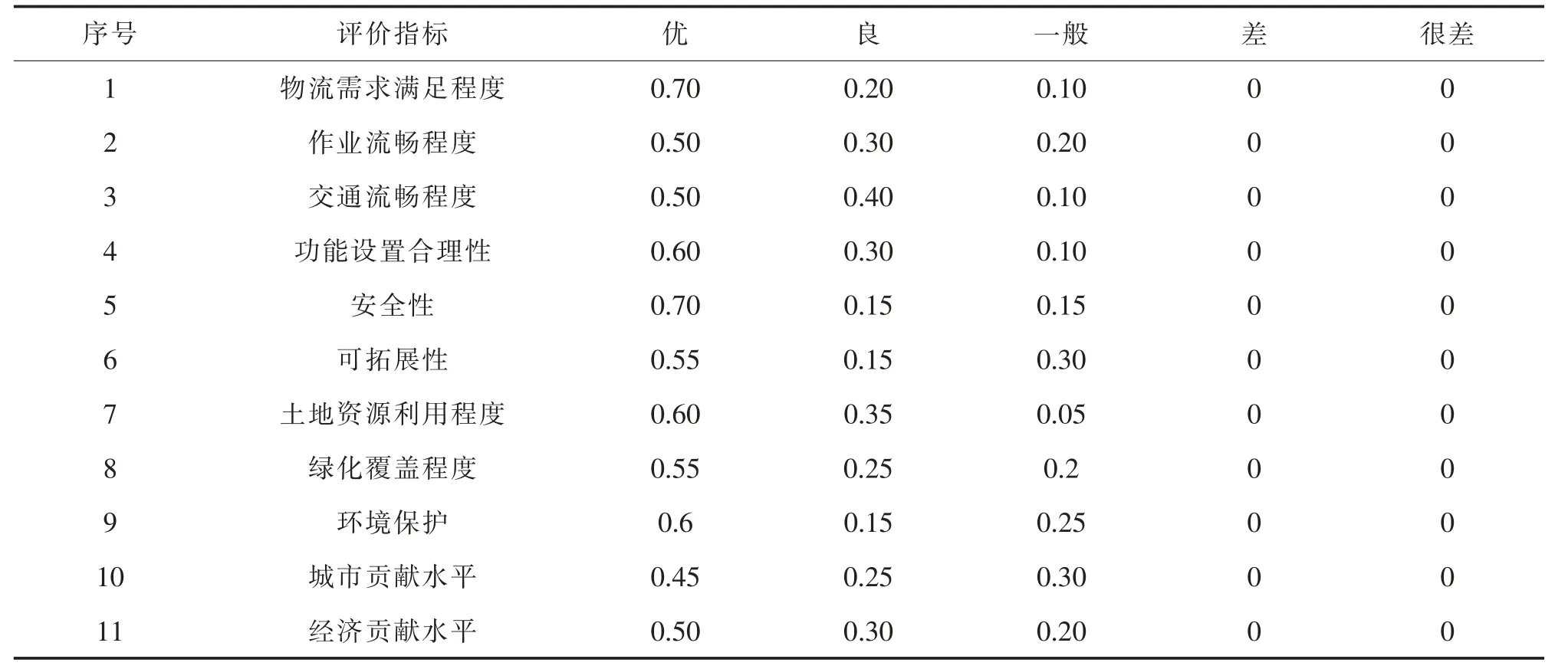
表7 R1*组合下的二级指标模糊隶属度统计表Tab.7 Statistical table of fuzzy membership degree of secondary indicators under R1*combination
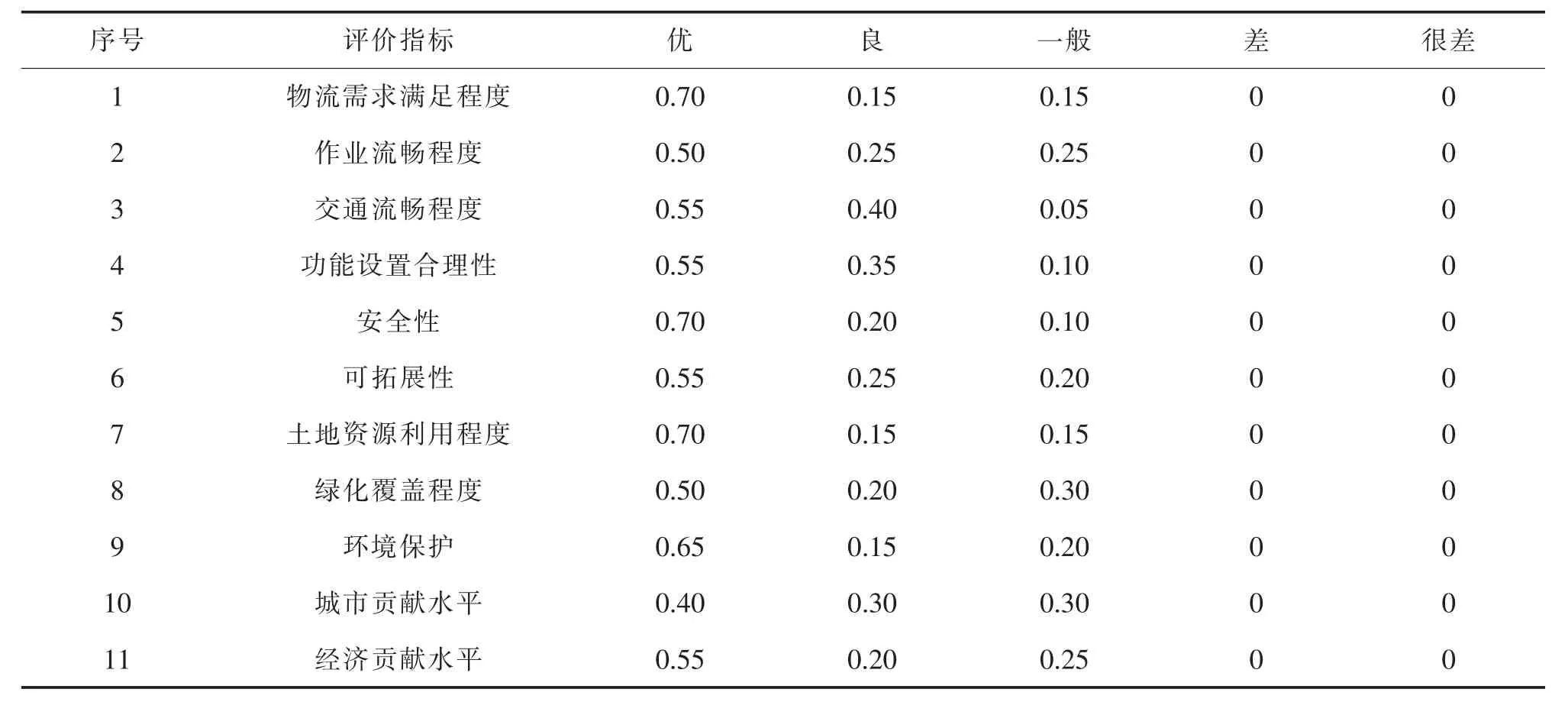
表8 R2*组合下的二级指标模糊隶属度统计表Tab.8 Statistical table of fuzzy membership degree of secondary indicators under R2*combination
设定S 市西站物流中心布局方案评价指标集U=(U1,U2,U3,U4),评语集V=(V1,V2,V3,V4,V5)依次代表“优”、“良”、“一般”、“差”、“很差”,且设S=(90,80,70,60,50)T,可计算得
B1=W·R1=(0.552032,0.257582,0.191296,0,0)
B2=W·R2=(0.564862,0.250412,0.184637,0,0)
F1=B1·S=83.61016
F2=B2·S=83.79506
按照最大隶属原则,可知R1*、R2*所对应的S 市西站物流中心布局方案最终评价等级均为“优”;继续按照系统总得分排序,可知R2*所对应的方案较R1*相比更优,因此,R2*所对应的布局方案即为S 市西站物流中心最终布局方案。
4 结语
本文提出了基于改进SLP 的铁路物流中心功能区布局方法,以相关关系最大、总搬运成本最小为目标建立多目标函数,并在几何和功能两方面进行约束设置,通过NSGA-Ⅱ遗传算法进行求解,得到最优布局方案解集。最后,运用AHP 模糊综合评价法对拟最优方案进行评价,得到最终的功能区布局方案。并以S 市铁路物流中心为案例,验证了本文提出方法的可行性。本文提出的铁路物流中心功能区布局方法,充分考虑了铁路物流中心货物品类及作业流程特点,在布局模型和求解算法上进行改进,更加科学合理。该方法的提出有利于改善铁路物流中心内部布局结构,提升铁路物流中心整体运营效率,对铁路物流中心及铁路货运的发展具有实际参考意义。

