基于内插多相滤波的短波数字移相算法

朱凌刚，娄景艺，梁步阁，杨德贵

(中南大学 航空航天学院 雷达探测制导实验室，湖南 长沙410083)

0 引言

数字波束成型(Digital Beam Forming,DBF)和相控阵是短波通信的一个重要发展方向，在特殊通信和目标侦听领域[1-5]有着广泛应用需求。

早期的相控阵在天线单元上安装移相器控制各通道相位，相控阵波束随着相控阵工作频率变化而偏移，严重限制天线瞬时带宽[6-8]。

为提高移相精度和方向图指向精度，延迟线取代了移相器，延迟线的延时一定且与频率无关。已有的延迟线研究主要集中在材料研究、电路设计、结构形式设计等方面，如声体波和声表面波延迟线、静磁波延迟线、超导延迟线、光纤延迟线等[9-12]。

尽管近年来一些研究者完成了数十皮秒级别的延迟线电路仿真[13]，但在工程实践中，上述延迟线技术存在结构换能效率低、结构复杂、成本高昂和传输损失等问题[14]。随着数字技术的发展，人们开始使用数字滤波[15-17]方法实现移相。

结合短波通信工程实际情况，提出一种结合数字延迟线和内插多相滤波的算法，在不提高延迟线采样率的前提下使用数字滤波进行信号处理，使用Matlab仿真验证。

1 短波发信线阵模型

短波发信阵列利用DBF技术，对各阵元输出进行加权和延迟，以形成空间指向性，通过改变天线阵中各基本单元激励信号的相位，对空域进行大角度扫描。

以图1所示的均匀线阵为例，设相邻天线间间距为d，与远场的通信目标夹角为θ。为方便讨论，假设所有天线阵元近似为各向同性点源。以发信机1号的天线为参考天线，可知n号天线到目标参考平面的距离比1号天线少(n-1)dcosθ。为使各路信号到达参考面时同相，以达到最优合成效果，设各路天线发射的短波信号为y=u(t)ej(2πft+φ(t))，其中u(t)为幅度，f为频率，φ(t)为相位，相较于参考天线，第i路信号的时间延迟和相位延迟应分别为：

(1)

通过控制发信机补偿时间或相位延迟即可实现在远场参考面处的波束合成。

图1 线阵波束合成Fig.1 Line array beam

波束合成技术的重点在于准确控制各路信号相位，以适应方向图需求。对于准确性来说，应以相移精度即最小移相单位来衡量。对于频率为f0的射频信号，其最小相移σmin和采样率fs关系如式(2)所示：

(2)

由式(2)可知，最小相移σmin与射频信号频率f0成正比，与采样率fs成反比;σmin越小,表明相移精度越高。

2 传统基于数字延迟线的移相方法

传统的基于数字延迟线的移相基本过程是先计算各天线与基准天线的相对相位值，再对馈入天线的射频信号进行内插升采样以提高时域分辨率，最后控制数字延迟实现数字移相。移相精度和数字延迟线的采样率成反比，只要数字延迟线采样率足够大，即时域分辨率足够小，理论上就可以实现任意相位的控制。

根据式(2)，可以计算出给定数字延迟线采样率下，为达到需要的移相精度所需要提升的采样率倍数，称为内插倍数。

为使移相精度达到1°，在100 MHz延迟线采样率下，不同频率短波信号需内插的倍数如图2所示。

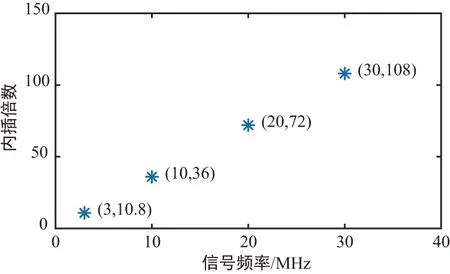
图2 100 MHz延迟线采样率下所需内插倍数Fig.2 Interpolation multiples required at 100 MHz delay line sample rate

当天线射频信号频率f=30 MHz且移相精度σmin为1°时，理论上需要采样率10.8 GHz，即对数字延迟线采样率内插108倍。此处存在两个问题：

① 受数字延迟线技术和成本限制，单纯依靠更高采样率的数字延迟线进行移相的方法不可取；

② 随着采样率的n倍提升，存储器的内存也需增大同样倍数，大量信号的读取写入导致无法实现信号的实时处理。

因此，需要改进方法，一方面既保证较高的内插倍数，另一方面尽可能使运算在低采样率与数据量下完成，可通过多相滤波算法划分多相结构来完成这一目标。

3 多相滤波算法

3.1 零值内插

将序列信号x(n)的采样率从fs提升到Ifs(其中为正整数)的过程称为插值。理论上，可以将序列经AD变成模拟信号后再经AD以Ifs抽样率进行重采样，但是AD会引入失真和量化误差，因而实际应用中不加采用，而是采用图3所示的零值内插方法。

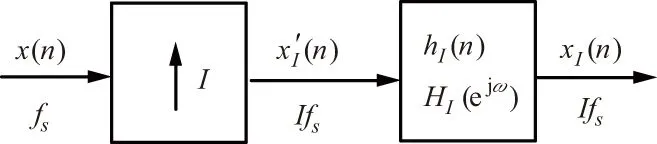
图3 内插系统框图Fig.3 Block diagram of the interpolated system

图3第一部分是零值插值器，表示在x(n)的相邻两个采样点间插入(I-1)个零值点，插入后采样率提高，因而也称为上采样器，其输出为x′(n)；第二部分是一个低通滤波器hI(n)，用于滤除第一步插值带来的频域镜像分量。

3.2 抽取与多相结构

将序列信号x(n)的采样率从fs降低到fs/D(其中D为正整数)的过程称为x(n)的D倍抽取，如图4所示。

图4 抽取系统框图Fig.4 Block diagram of the extraction system

抽取过程分为抗混叠滤波和抽取两步。这是因为抽取后的采样率如果低于信号最高频率的2倍，则会产生信号的频域混叠，因此在抽取器前需要进行抗混叠滤波。该抗混叠滤波器采用FIR滤波器实现，其系统函数为：

(3)

当滤波器系数总数为N、抽取比为D时，若采用直接型FIR结构，其缺点是滤波器h(n)工作在高采样率fs下，x(n)的每一样值都要与所有滤波器系数相乘,但抽取比D只需一个值，因而浪费多次乘法。为提高运算效率，利用线性时不变系统的交换律，先对输入数据x(n)进行D取1的抽取，再与各系数h(n)相乘，随后相加，运算均在低采样率fs/D下进行。

考虑加防混叠滤波器的抽取系统如下：

(4)

由式(4)可知，与h(0)相乘的是抽取后的x(Dn),其输入端对应信号为{x(n),x(n+D),x(n+2D),…}，与h(1)相乘的是抽取后的x(Dn-1)，对应信号为{x(n-1),x(n-1+D),x(n-1+2D),…},依次类推，可以发现抽取结构分成了D组，即得到了多相结构。取N=DQ，在式(4)中令k=Dm+i，其中i=0,1,…,D-1，m=0,1,…Q-1，得：

(5)

根据式(5)，可以把抽取结构分为D组，且每一组都是相似的Q个系数的FIR系统，当采用D=1的抽取器时，有D组子滤波器，可表示为：

gi(m)=h(Dm+i),i=0,1,2,…D-1,

m=0,1,…,Q-1，

(6)

则原滤波器可表示为：

(7)

式中，gi(m)为工作在低采样率下的线性时不变滤波器，称为多相滤波器，抽取器多相结构如图5示。

图5 抽取器多相结构Fig.5 Polyphase structure of the extractor

4 内插多相滤波的移相算法

基于上述问题，将数字延迟线和内插多相滤波结合起来，提出一种结合数字延迟线和多相滤波的数字移相算法。如图6所示，先利用数字延迟线完成部分延时，再将多相抽取后的FIR滤波器系数和天线射频信号卷积达到n倍内插效果，信号只需与分相滤波器的抽头卷积即可完成延时，从而完成相位控制，同时降低数据量。算法中，总延时分为粗延时和细延时两部分，粗延时是数字延迟线精度的整数倍，可直接用数字延迟线完成；细延时是比数字延迟线精度更小的部分，可采用多相滤波的方法来完成。

图6 算法流程示意图Fig.6 Schematic diagram of algorithm flow

算法流程：

① 根据内插倍数、通带波纹、通带最大衰减和阻带最小衰减计算生成内插滤波器系数向量num,按内插倍数分解num得到重新排序后的滤波器系数矩阵num1；

② 计算各阵元的延时，按序存入Nx1的向量τ，N是阵列阵元数；

③ 将时延向量τ分为粗延时向量cu和细延时向量xi，其中cu对应于时延τ中所包含的整数个系统采样周期(即数字延迟线采样周期)的部分，xi对应于时延τ中不足一个采样周期的部分；

④ 将入射信号按时间序列存储在数据存储器中；

⑤ 根据所需粗延时cu，用数字延迟线对射频信号进行延时处理得到粗延时后信号temp；

⑥ 根据所需细延时xi，使用num1对信号temp进行滤波，得到细延时后信号firout，即为移相后的天线发射信号，移相完成。

5 仿真与结果

设一个短波阵列发射天线信号频率为2 MHz，阵元间距为1/3波长,采样率为100 MHz，阵列与远场通信目标夹角为77°。经计算，相邻阵元间需延时37.5 ns，要求移精度为1°。

在进行内插滤波时，考虑到需要实现0.1 ns的延时，采样率至少为10 GHz，因此FIR滤波器设置如下：采样率为10 GHz，通带截止频率为30 MHz，阻带截止频率为50 MHz，阻带衰减为80 dB，滤波器阶数为1 600 阶。利用Matlab自带的Fdatool设计该滤波器，采用等波纹最优设计方法。

将生成的滤波器系数保存到workspace，是一个1×1 600的向量。由于信号内插了100倍，根据抽取的多相结构原理，从第一个抽头系数开始，每隔100个取一个系数，放入第一列，最后组成一个16×100的系数矩阵，得到各分相滤波器，如图7所示。

设此时延迟线采样率为100 MHz，则数字延迟线精度为10 ns，按照算法第二步，将37.5 ns分为粗延时30 ns、细延时7.5 ns。10 GHz滤波器采样率下，由图5可知，每一组分相滤波器比前一组延时0.1 ns，若需要延迟37.5 ns，可先延时3个数字延迟线采样周期，再与第75组滤波器系数进行卷积得到细延时，最终的仿真结果如图8所示，取第200～300个采样点区间表示。

图7 分组后的滤波器系数Fig.7 Filter coefficients after grouping

图8 移相仿真结果Fig.8 Phase shift simulation results

结论：

① 延迟信号比原信号约延迟37.5 ns，基本验证了算法的有效性；

② 在运算过程中，多相结构将卷积的滤波器抽头系数缩小为原来的1/100，使得输出的数据量和原信号数据量保持一致，从而保证了运算的实时性；

③ 通过内插多相滤波实现了0.1 ns的延时精度，突破了100 MHz数字延迟线的精度限制。

6 结束语

在短波发信阵列波束合成和数字信号处理方法的基础上，针对短波天线数字信号合成中的移相环节，介绍了一种数字移相算法。该算法克服了传统数字移相算法移相精度受信号采样率限制的缺陷，实现了信号的高精度数字移相。在Matlab中进行了仿真计算，结果表明了算法的正确性。该算法具有计算过程简单且不受系统采样率限制的优点，后续还需进一步研究滤波器改进、波束合成方向图误差分析等内容。