复杂电磁环境下的弱干扰信号检测算法
徐少波,张明程,陈 强,宋 肖,张 丹
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
全球导航卫星系统(Global Navigation Satellite System,GNSS)已成为人类从事政治、科学、经济和军事活动必不可少的信息技术。但是在复杂的电磁干扰环境中,其易损性和脆弱性也逐步显现出来,导航系统的连续性、完好性和可用性方面面临巨大挑战,因此对干扰信号的能量、频段及干扰类型等信息实时进行检测[1-2],尤其是影响阵列处理自由度[3]且不易检测的弱干扰信号[4],成为导航信号处理领域亟待解决的关键问题。
根据对干扰处理方式的差异,传统的干扰检测技术主要分为时域干扰检测技术[5]和变换域干扰检测技术[6]两大类,此外关于接收机相关的干扰检测[7]也得到了广泛应用。在时域干扰检测技术中,干扰检测算法大多是盲检测算法,主要是通过检测接收信号的能量大小来判断是否包含干扰信号。这种盲干扰检测算法具有普遍的适用性,在变换域干扰检测技术中,通过对接收信号中各种成分的分析,从而得到变换域特征作为干扰检测的依据。根据参考域的不同,将变换域干扰检测技术分为频域变换[8]、小波变换、时频变换以及高阶累积量[9]等干扰检测技术。基于频域干扰检测,文献[10]改进了传统的固定门限干扰检测算法,对干扰谱线进行循环估计,提升了宽带干扰的检测性能;文献[11]提出了一种将重排技术与小波变换相结合的干扰检测方法,针对GNSS 接收机中的干扰信号,可以有效地处理时频分辨率和时频分布等问题,提高GNSS 接收机的干扰检测能力。基于接收机相关干扰检测的主要思想是通过 GNSS 相关器的输出波形、AGC 增益、载波相位波动及载噪比等信息来实现干扰检测。文献[12]通过在接收机信号捕获与跟踪过程中增加噪声功率估计功能,并对噪声功率设定检测门限,即可对多种干扰信号实现有效检测。虽然通过提取相关器后的参数可以有针对性地实现对某种干扰的高效检测,但是由于在解扩过程中会丢失部分频谱信息,增加了干扰类型估计的难度。
然而上述算法对弱干扰信号的估计性能较差,尤其是存在强压制干扰环境下的弱干扰信号检测性能将严重下降。本文利用阵列信号处理中的空域与频域联合处理后的特征值分布特性,将被压制在强干扰信号下的弱信号分离出来,同时可进行定量的信号参数检测,仿真结果表明,存在阵列幅相误差时本文算法仍能进行有效的干扰检测。
1 系统模型与检测算法
1.1 空域-频域信号处理模型
考虑M元均匀圆阵且假设阵元均为各向同性阵元、阵元间不存在互耦。中心频率fc、带宽为BW的期望信号s(t)=[s1(t),s2(t),…,sD(t)]T在观测时间段T0保持平稳特性,且其频谱密度函数表示为Ps(f),其中|f|∈F=|fc-BW/2,fc+BW/2|。Ps(f)是D×D维的共轭正定矩阵。噪声场与期望信号相对独立,且其频谱密度函数为M×M维的Pn(f)。M元阵列接收数据x(t)的频谱密度函数可表示为:
Px(f)=A(f,θ)Ps(f)AH(f,θ)+Pn(f),
(1)
式中,A(f,θ)=[a(f,θ1),a(f,θ2),…,a(f,θD)]为M×D维对应频点f的阵列导向矢量矩阵,a(f,θi) 对应来自方向θi的第i个信源的导向矢量[13]。
首先将指定时间段T0内阵列输出矩阵x(t)在时域上均匀分为K段,每个数据段通过无叠加的分段DFT运算转换为N点频域分量,同时假设分解的各个频域分量相对独立[14]。将第k段数据段对应的第i个频域分量表示为xk(fi),其中k=1,2,…,K,i=1,2,…,N,对应的协方差矩阵可表示为:
Rx(fi)≈Px(fi)=A(fi,θ)Ps(fi)AH(fi,θ)+Pn(fi)。
(2)
Rx(fi) 为阵列协方差矩阵的经典表示形式,但是当输入信号存在相干信源时,阵列导向矢量矩阵为广义对称矩阵,即满足下式:
A(f,θ)=J·A*(f,θ),
(3)
式中,J为副对角线为1的置换矩阵,定义如下:

(4)
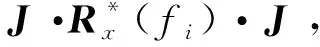
(5)
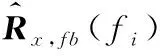
(6)

当所有频域分量对应的协方差矩阵都计算并进行特征值分解后,在整个频域段可以得到M条特征值的包络曲线,由此可以很清晰地分离出强干扰压制下的弱干扰信号,同时可对接收干扰信号的个数、带宽等参数信息进行进一步估算。图1为四阵元天线接收一个强宽带干扰和一个弱窄带干扰时的特征值分布曲线,可见对于不同的干扰分量,都相应使得特征值在噪声分量基础上的提升,进而清晰地将在频谱上被淹没的弱窄带干扰检测出来。

图1 基于阵列空域-频域联合处理的特征值分布曲线Fig.1 Distribution curve of eigenvalues based on the joint process in space-frequency domain
1.2 子空间快速分解算法
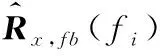

具体步骤如下:
步骤1:给定Hermitian矩阵A=Rx(fi);r0=f(单位范数向量),即‖r0‖=1;β0=1;j=0。
步骤2:执行m次三Lanczos迭代:
while(βj≠0)
qj+1=rj/βj;
j=j+1;
rj=Aqj-αjqj-βj-1qj-1;
βj=‖rj‖2
end
步骤3:在三Lanczos迭代的第m步将得到m个正交向量,即Lanczos基Qm=[q1,q2,…,qm],进而构造m×m三对角矩阵Tm,并求其特征值,得到Rx(fi)特征值的渐进等价估计。
1.3 干扰信号检测算法
通过空域-频域处理后,功率较强的干扰分量能够直观地与噪声分量进行分离,为进一步对干扰参数进行量化[16],本文提出一种通过计算特征值分布曲线的平滑斜率分析法进行干扰检测,该算法不但能够有效分离出强干扰条件下的弱信号,而且适用范围更广。
首先计算特征值λi的分布曲线的平滑斜率值:
(7)
式中,i∈[1,M],k∈[1,K-U],累积变量参数U是基于统计估计的,如果数值过大,在检测边界会出现模糊估计;过小则会导致过高的虚警概率。如果得到的斜率曲线SPi(k)趋于平滑,则说明该分量只有热噪声的存在,而当曲线出现骤增或骤降,则得到干扰信号的检测边界。
对于任意一条λi的包络曲线,对应的干扰信号分量的带宽可通过下式得到:
Bi=max(SPi)-min(SPi),i∈[1,M]。
(8)
很明显,入射信号中心频率为Bi/2处,而且特征值斜率分布曲线中急剧上升或下降的突变点同样可以用来估计干扰个数。
2 仿真试验和性能分析
仿真条件:采用阵元数为4的均匀圆阵,阵元间距为导航接收信号的半波长,假设卫星的方位角和俯仰角分别在0°~360°和0°~90°的空间范围内服从均匀随机分布。假设有三个干扰信号,各干扰信号的带宽、干噪比(Interference Noise Ratio,INR)、方位角和俯仰角参数设置如表1所示。
表1 干扰信号的参数设置
Tab.1 Parameters of interference signals

干扰带宽/MHz干噪比/dBm方位角/(°)俯仰角/(°)J120605090J254040130J30.52030210
采样频率为62 MHz,卫星及干扰信号的数字中频为15.48 MHz,500次蒙特卡洛试验。为综合考虑计算复杂度和检测精度,将数据段设为8段,每个数据段进行512点FFT运算。以下试验均采用此组仿真参数,不再赘述。
2.1 无幅相误差时干扰信号的检测仿真性能
图2是不同的特征值分量在整个频域范围内的分布曲线,可以看出在无幅相误差时,干扰能量较弱的干扰信号J3能够清晰地从带宽、功率都较高的干扰信号J1和J2中分离出来,同时将高于噪声分量的三个信号分量判定为干扰信号,且能够估算出其中心频点和带宽等信息。
图3~图5是不同特征值分布包络对应的平滑斜率值,可以看出无幅相误差时,包含较高特征值分量的λ1,λ2,λ3的斜率变化曲线中的极大值点和极小值点之间频域段即为干扰信号J1,J2,J3的带宽:
λ1:20 MHz宽带信号分量;
λ2:5 MHz窄带信号分量;
λ3:0.5 MHz单音干扰信号分量;
λ4:白噪声分量。
此外,在斜率变化曲线的极大值点与极小值点的中心位置即为中心频率15.48 MHz,进而得到接收干扰尤其是强干扰压制下的弱干扰信号的相关参数信息。
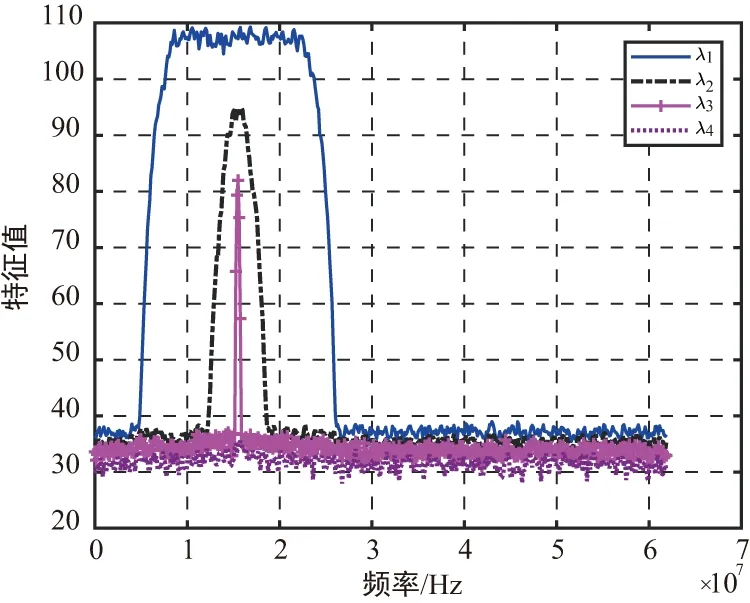
图2 不同干扰信号分量对应的特征值分布曲线图Fig.2 Distribution curve of eigenvalues of different interference signals

图3 基于平滑斜率分析法的λ1的干扰检测结果Fig.3 Detecting result of λ1 based on smooth slope analysis

图4 基于平滑斜率分析法的λ2的干扰检测结果Fig.4 Detecting result of λ2 based on smooth slope analysis
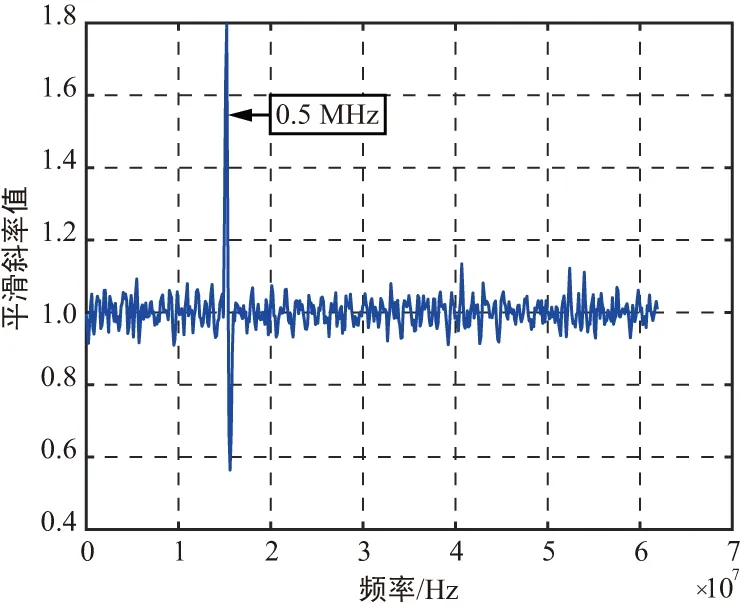
图5 基于平滑斜率分析法的λ3的干扰检测结果Fig.5 Detecting result of λ3 based on smooth slope analysis
2.2 存在幅相误差时干扰信号的检测仿真性能
上节对不存在幅相误差时弱干扰信号的检测性能进行了仿真分析。但在实际应用中,器件发热和老化,天线阵周围环境的变化,阵元天线安装误差等,都会引起通道幅相特性的变化,因此本试验主要分析存在幅相误差时干扰检测算法的有效性。为简化说明,以干扰J1为例,同时为了进一步验证对弱干扰信号的检测性能,将干扰J1的干噪比改为20 dBm。
为详细说明幅相误差的影响,本试验仍以四阵元阵列为例,通道之间的幅相不一致性随时间有一定的变化,但是变化过程十分缓慢,在形成相关矩阵时,可视为固定不变的。其幅相误差系数矩阵数学模型设为:
(9)
式中,Γ=diag(b1ejφ1,b2ejφ2,…,bMejφM)为通道不一致系数矩阵,bi和φi分别表示通道间的幅度和相位误差。假设幅度和相位误差分别服从正太分N(1,σ2)和N(0,σ2)。对于接收天线阵列而言,其接收数据的数学模型为:
X(n)=Γ·A·S(n)+N(n),
(10)

图6为幅相误差的方差分别为0.2和0.4时,同无误差的归一化特征值分布情况对比图,可以清晰地看到随着误差的增大,干扰对应的大特征值变化不大,但是噪声对应的小特征值有所上升,导致干扰和信号之间的区分界限变得模糊,大特征值同小特征值的归一化差值从0.67降到约0.6,进而导致干扰检测虚警概率的提升。

图6 不同误差情况下的特征值分布情况Fig.6 Eigenvalues distribution with different errors
图7展示了不同误差情况下干扰检测的斜率曲线。斜率曲线的峰值受到误差的影响有所下降,相对于无误差的情况,幅相误差的方差为0.2和0.4时,斜率峰值从0.5分别降到了0.4和0.3。但是由于平滑的效应,仍然能够得到干扰个数、带宽和中心频点等干扰参数有效的检测结果。
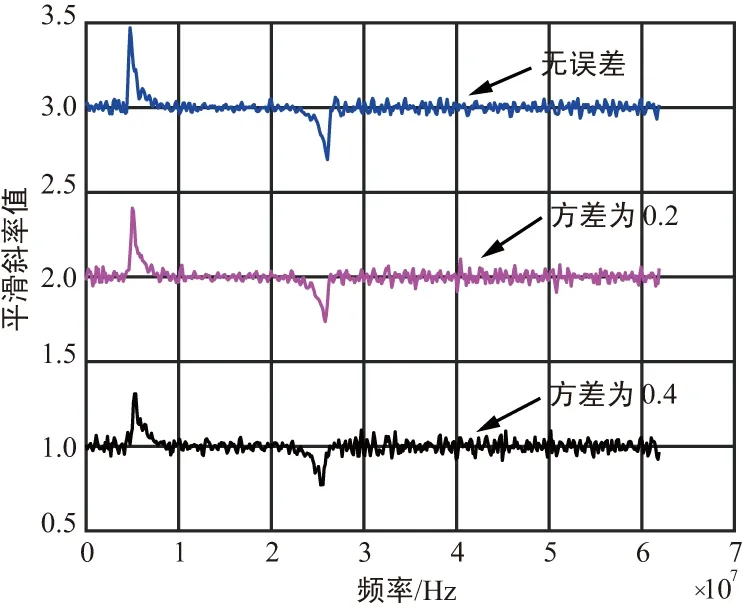
图7 不同误差情况下的干扰检测结果Fig.7 Interference detecting result with different errors
3 结束语
为解决复杂电磁环境下弱干扰信号检测的问题,提出了基于空域阵列信号处理的先分时后分频的检测算法,通过观测导航信号频带内不同特征值分布曲线可准确分离出强干扰环境下的弱信号分量,同时通过特征值分布的斜率方差可进一步估计干扰信号的其他参数。该算法不需要进行复杂的信源个数估计,且适用于不同的天线阵型,仿真结果表明该算法在存在幅相误差条件下仍然能够进行有效的干扰信号检测,具有一定的稳健性和适用性。

