一种低复杂度的无线虚拟网络资源分配策略
曾菊玲,张春雷,盛明哲,夏 凌,解 冰
(1.三峡大学,湖北 宜昌 443002;2.中国联通研究院,北京 100032;3.天翼电信终端有限公司,北京 100032)
0 引言
为了提供面向应用、开放灵活、可编程和易维护的服务,未来5G将采用虚拟网络架构[1-3]。虚拟化技术在提供高效及灵活组网的同时,也增大了技术实现复杂度,特别是资源分配更加复杂。由于虚拟化技术导致虚拟资源层或移动虚拟网络操作层(Mobile Virtual Network Operators,MVNOs)的出现,使得原本在基础设施提供层(Infrastructure Providers,InPs)和用户(Users,UEs)之间进行的资源分配,变为MVNOs向InPs购买或租用无线资源,再向UEs提供服务。资源提供途径和各方收益都变得更加复杂,特别考虑到无线信道的实时多变特性,采用自适应资源分配策略时,虽然获得更大收益,但中间层MVNOs的存在,也将自适应策略变得更加复杂。
对于无线虚拟网络资源分配,目前已有很多相关研究。文献[4-5]提出了InPs与用户之间直接分配资源的方法,由于MVNOs未参与其中,不能实现真正虚拟化。文献[6]提出了InPs-MVNOs-UEs三级架构,但没有给出具体算法。文献[7-8]采用InPs-MVNOs-UEs三级架构,提出了基于三层架构的二级联合分层拍卖机制资源,整体效用最优,但个体效用非最优,中心控制方式导致计算复杂度较大。文献[9-10]采用Stackelberg博弈和McAfee拍卖两阶段联合机制对虚拟网络功率进行了分配,但不能进行切片选择。文献[11]采用分层博弈研究了超密集蜂窝网络资源分配问题,但只能保证效用最大,没有讨论频谱效率优化问题。文献[12]提出了InPs-MVNOs以及MVNOs-UEs分层匹配博弈,然后循环迭代直至收敛的分层匹配博弈机制,有效解决了三级架构下业务选择和资源购买两阶段联合优化问题(简称联合分层博弈),但上、下层间循环迭代导致计算量过大,且没有考虑到对时变无线信道的跟踪,导致资源利用率较低,同时,两层多对一匹配不能实现用户与切片精确匹配,片内资源优化无法实现。事实上,在虚拟网络中,MVNOs作为独立运营商,向UEs提供业务与向InPs购买资源是独立的,上、下两层博弈可以独自进行,不需要循环迭代,通过两层独立的多对一匹配博弈,实现用户组与切片组的匹配,较大地降低复杂度。但用户组与切片组匹配不能实现用户与切片的一对一精确匹配,且分层匹配博弈只能实现无线虚拟网络中资源分配的效用最大化,不能保证频谱效率最优。因此,需要在分层匹配博弈之后再次进行无线资源分配,以保证精确匹配和频谱效率最大化,目前还未见研究二者结合的文献。自适应无线信道的资源分配策略在OFDMA网络中研究较多,通过为用户分配较好子信道和适应于信道的功率,提高系统无线资源利用率,文献[13-15]提出了一种低复杂度的比例公平的资源分配策略,具有较好效果。InPs为MVNOs分配切片及功率的过程,恰好类似于OFDMA为用户分配子载波及其功率的过程,因此,可借用之。
本文提出一种低复杂度的分层匹配博弈结合比例公平的无线虚拟网络资源分配策略。首先,采用2层独立的分层匹配博弈避免双层循环导致的较高计算复杂度,博弈下层为UEs与MVNOs构成的多对一匹配,实现UEs对MVNOs依效用选择,上层为MVNOs与InPs构成的多对一匹配,实现MVNOs对切片依效用选择,通过二层博弈,最终实现用户组与切片组效用最高匹配。然后,在匹配InPs与MVNOs间采用比例公平的资源分配策略,实现用户与切片的精确匹配,并在比例公平的条件下,实现频谱效率最大。
1 系统模型
图1是三级架构的无线虚拟网络。最高层是InPs,每个InP包含一个基站,基站的每一个信道抽象成一个切片,一个InP包含NS个切片。假定每个切片带宽相同,功率可调,假定一个切片只能同时服务一个MVNO,对不同的MVNOs收取不同报酬。中间层是MVNOs,MVNOs通过独立合约,根据网络状况和资源价格等因素,动态地向InPs购买无线资源,且一个MVNO可以购买多个切片,MVNOs根据服务等级等因素以不同的价格向终端用户提供服务。最底层是UEs,以不同价格向MVNOs提出带宽请求,一个用户可向多个MVNOs提出服务申请。
资源分配的过程为: UEs向MVNOs提出带宽申请,再由向InPs申请网络切片。
2 分层匹配博弈
2.1 多对一匹配博弈
多对一匹配是指匹配双方中的一方B能接纳另一方的A中多个成员,而A的成员只能在B中选择一个成员。
定义1:一个匹配μ是从集合A∪B到A∪B所有子集构成的集合的一个映射,对所有a∈A和所有b∈B,有
μ(a)∈B∪∅,μ(b)⊆A,
(1)
B=μ(a)⟺a∈μ(b)。
(2)
一个匹配是稳定的,每一个参与者的匹配对象都是可接受的,且不存在一对未发生匹配的参与者,他们互相偏好与对方发生匹配。
定义2:如果匹配μ满足对所有的个体a∈A∪B,μ(a)R(a)φ,对所有的b∈B,Cb(μ(b))=μ(b),称μ是一个稳定匹配。其中,μ(a)R(a)φ表示A中的元素a在B中的映射不是空集,Cb(a)表示元素a在B中的选择集。
稳定匹配存在的条件:A或B中所有个体都存在严格偏好。
对于稳定匹配,可采用拒绝——接收算法求解。
2.2 用户UEs与MVNO间多对一匹配博弈
在下层博弈, UEs向MVNOs购买带宽,得到服务,达成自身满意度,1个UE只能向1个MVNO购买带宽,1个MVNO可向多个UEs提供带宽服务。UEs以不同价格向MVNOs购买带宽,同理,MVNO向不同UE提供带宽时,具有不同收益。UEs与MVNOs双方应根据效用最大原则选择对方,因此,构成UEs为租用者、MVNOs为供给者的多对一匹配。
假定第m个MVNO(m∈M)向一组UEs提供服务,Κ=UmΚm为总的UEs数目,Km表示第m个MVNO服务的用户数,用符号|Κ|表示集合K的基数,为了简单,用K表示用户总数,Um表示Km的并集。
对于无线网络的UEs,主要考虑数据流量,是尽力而为业务,带宽越大,传输的数据流量越大,用户满意度越高,满意度函数为:
(3)
式中,Bk,m为MVNOs提供给UEs的带宽,s1为正常数,Bmax为达到最大效用的带宽,受相关信道容量及通过率限制。
第k个UE从MVNOm购买带宽获得的效用为:
Ek,m=Udata(Bk,m)dk-λk,mBk,mdk,
(4)
式中,dk为UEk对切片的需求数;λk,m为第k个UE向MVNOm购买带宽的价格且各不相同,Bk,m为第k个UE向第m个MVNO购买的带宽;因此, UEs的优化目标为:
(5)
式中,uk,m=1表示第k个UE购买MVNOm的带宽。
对于第m个MVNO,向第k个UE提供带宽获得的报酬,
(6)
式中,μm,k为第m个MVNO向第k个UE提供带宽的价格且各不相同。特别说明的是,在式(6)中,计算MVNO的报酬时,本应减掉MVNO为向第k个UE提供带宽而向INP购买物理资源需要付出的成本,但考虑到那样做会将上、下两层博弈耦合,相互影响,系统达到博弈稳定的计算复杂度太高。而事实上,MVNOs作为虚拟中间商,向用户提供带宽与向INP购买物理资源可作为两个独立的过程,因此,忽略了购买物理资源的成本。
因此,第m个MVNO的优化函数为:
(7)

为了联合求解式(5)和式(7),得出第k个UE与MVNO的最佳匹配uk,m,UEs与MVNO间构成多对一匹配,其中UEs的偏好函数为式(4),MVNO的偏好函数为式(6),步骤如下。
步骤1:任意UEk向可接受的最偏好的MVNOm递交服务申请;每一个MVNO根据已定指标数在收到所有申请中留下本集中的申请(每个MVNO可选择多个用户),拒绝其他用户。
步骤k:每一个未匹配的UEk′向还未拒绝过它的、最偏好的MVNOm′递交服务申请;每一个MVNOm′根据已定指标,在收到的剩下所有用户申请中留下它选择集中的申请,拒绝所有其他申请。
当没有拒绝发生时,算法结束。每一个MVNO服务它在算法最后一步中接受的所有用户,算法产生一个匹配。
2.3 InPs与MVNOs间多对一匹配博弈
在上层博弈,InPs向MVNOs提供物理资源。假定物理资源的单位是切片,每切片的带宽已定并相等,因此,InPs向MVNOs提供切片并分配功率,但二者同时进行会导致计算复杂度太高。因此,首先假定各切片功率相等(平分总功率),假定1个切片只能提供给1个MVNO,而1个MVNO则可租用多个切片,InPs向MVNOs提供切片时,对不同的MVNO有不同收益。同理,MVNO租用不同切片时,具有不同价格。为了使各自效用最大,用户与MVNOs双方应根据偏好进行选择,因此,构成MVNOs为租用者、InPs为供给者且为多方的多对一匹配。
InPs与MVNOs多对一匹配博弈中, MVNO选择切片组,结合下层博弈,实现用户组选择切片组。确定MVNOs与InPs的连接关系后,采用功率受限的比例公平原则进行功率分配,以提高公平性和资源利用率,并适应信道变化。
对于MVNO,向InPs购买物理资源,向InP支付代价,其成本函数为:
(8)
式中,χm,n为MVNOm租用切片n时,向InPs购买功率的价格,购买的功率为pm,n,sm为MVNOm购买的切片总数。
因此,此时MVNOm的优化函数为:
(9)
式中,πm,n=1表示MVNOm购买切片n,mq表示MVNOm购买切片的指标。
对于InP,其向MVNO出售功率获得的收益为:
EInP,m,n=βm,npm,nsm,
(10)
式中,βm,n为InP提供切片功率的价格。
因此,InP的优化函数为:
(11)
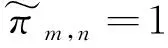
为了联合求解式(9)和式(11),得出InP与MVNO的最佳匹配πm,n, InP与MVNO构成多对一匹配,偏好函数分别为式(8)和式(10),当购买或出售功率的为价格随机时,式(8)和式(10)所示偏好是严格单调的,因此,匹配稳定解一定存在,即能得到效用最优的切片选择策略,稳定匹配可采用与2.2节末尾的一样的UEs与MVNO间多对一匹配拒绝接收算法。
3 比例公平的低复杂度功率分配策略
3.1 优化模型
当UEs-MVNOs,MVNOs-InPs两层多对一匹配完成后,形成用户组与切片组匹配。例如图1中,用户组(UE1,UE2)通过MVNO1与切片组(s1,s2)形成匹配组,无法得到UEs与切片间的一对一匹配关系,进而不能直接根据信道特点为切片分配功率。因此,匹配保证了特定价格下UEs,MVNOs,InPs三者收益最大,但不能保证频谱效率最高,需要进一步采用资源分配策略,实现UEs与InPs的精确匹配并使频谱效率最优。这一问题可以通过对系统频谱效率建模,并考虑到系统负载平衡,使优化问题首先速率比例公平来解决。
假定Km为与MVNOm匹配的一组用户,Sm为与MVNOm匹配的一组切片,即Km与Sm匹配,Hk,n为第k个UE与切片n之间的信道,pk,n为切片n分配给第k个UE时的功率,假定切片带宽相等,则对Km与Sm资源分配,建立如下优化模型:
(12)
(13)
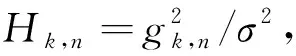
γk,n=pk,nHk,n。

(14)
式(12)是一个非线性整数联合优化问题,具有NP-hard的复杂度,不适合在线求解。
3.2 低复杂度策略
为了求解优化式(12),采用次优算法。贪婪定理是复杂度较低的搜索算法,首先由用户根据贪婪定理选择匹配组内的切片,然后根据KKT条件,求每切片的功率。
3.2.1 切片选择算法
为了简化式(12)的求解,将其解耦成两步:用户选择切片和切片功率分配。对于切片选择,式(12)是一个非凸问题,通过对ck,n整数放松,可变为凸优化问题,但计算复杂度太高,考虑到功率分布平坦时,多用户信道容量具有与单用户相同的注水效应,即在等功率条件下,用户选择信道质量较好的切片。因此,切片选择可采用贪婪定理:假定每切片功率相等,在迭代过程中每次让用户选择信道质量最好的切片,就能保证频谱效率最高,为了保证公平性,每次从速率比例最小的用户开始选择。贪婪定理不仅采用启发式方法解决了非凸整数NP-HARD最优化问题,而且搜索效率较高。
假定对于MVNOm,匹配的用户组为Km=∪kk,匹配的切片组为Sm=∪nn,假定每切片功率相等,令nk表示第k个用户选择的切片数,具体步骤如下:
①∀k∈(1,2,…Km),n∈(1,2,…Sm),令
ck,n=0,Rk=0,nk=0,p=Pm,TOT/N,
Km={1,2,…Km},Sm={1,2,…Sm}。
② fork=1 toKm
Sm=Sm/n*,ck,n*=1,nk=nk+1,
Rk=Rk+log2(1+pk,n*Hk,n*)。

Sm=Sm/n*,ck*,n*=1,nk*=nk*+1,
Rk*=Rk*+log2(1+pk*,n*Hk*,n*),
Ifnk*>dk*,Km/k*→Km。
3.2.2 切片功率分配策略
当用户选定切片之后,对于MVNOm连接的用户组和切片组,优化式(12)变为:
(15)
(16)
式中,nk表示第k个UE分到的切片数,Pm,tot表示MVNOm购买的总功率。
3.2.2.1 单个用户的切片间分配功率
对于式(15),应用拉格朗日乘数法则,对单个用户可得:
(17)
由此可得:
(18)
(19)
式中,pk表示MVNOm所连第k个UE的功率。
3.2.2.2 用户间分配功率
对所有用户,由式(15)可得:
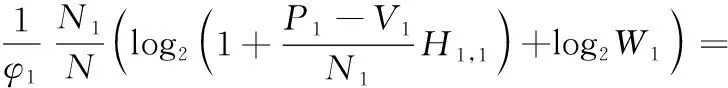
(20)
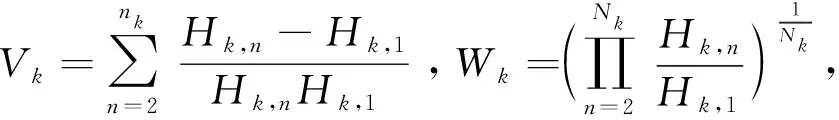
对式(16),有Km个变量,Km个非线性等式,求解计算量较大,为了简化,假定用户所需速率之比等于分到的切片数量之比。即:
Rk1:Rk2…Rkm=nk1:nk2…nkm=φ1:φ2…φkm,
则pk=(bk-P1)/ak,k,k=2,...,K,
(21)
(22)
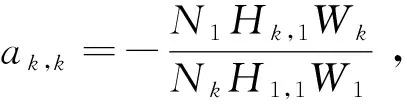
4 策略实现框图及复杂度分析
综合以上分析,本文策略的实现步骤如图2所示,可描述为:
① UEs与MVNOs间多对一匹配,实现UEs对MVNOs的选择;
② InPs与MVNOs间多对一匹配,实现切片对MVNOs的选择;
③ 通过步骤①~②,实现用户组与切片组的匹配;
④ 在每一组(用户组—切片组)内实现切片选择和功率分配。
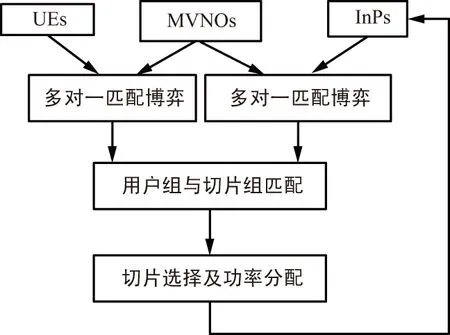
图2 策略实现框图Fig.2 Strategy diagram
可以看到,本文提出的匹配博弈结合比例公平的无线虚拟网络资源分配策略,低复杂度表现在以下几方面:
① 分层匹配博弈是两层独立的博弈,克服了文献[12]上、下两层循环迭代导致的大计算量。由于下层博弈中,对用户每次需要计算其对每个MVNO的偏好函数并排序,因此计算复杂度为O(kmlog2m),其中,k,m分别为UEs和MVNOs的数量,而每个MVNO都要对选择它的用户排序,计算复杂度为O(mqlog2mq),其中,mq为MVNOm的指标数,一般来说,k>>m,m>>mq,因此,下层博弈的计算复杂度为O(kmlog2m)。同理,上层博弈的计算复杂度为O(Nmlog2m),其中,N为切片数量,可见,上、下层多对一匹配博弈分别小于一对一匹配博弈的复杂度O(kNlog2N)。
② 对于比例公平资源分配策略,基于贪婪定理的切片选择计算复杂度为O(kmqNmqlog2Nmq),其中,kmq,Nmq分别是MVNOm连接的用户数和切片数,相比在全网进行切片选择的计算复杂度O(kNlog2N)要小很多。
③ 对于比例公平资源分配策略,功率分配策略将一个不可解的非凸优化问题用一步算法即可实现,而且计算复杂度仅为O(kmq)。①~③说明本文策略在图2所示各个环节的计算复杂度低于联合分层博弈。
④ 信道反馈信息简化,文献[12]在用户与MVNO的博弈中,构造了MVNOm-InPn对mn,并在偏好函数中引入了信道信息,即每个用户需要知道所有切片的信道信息。而本文所提策略中,用户只需知道匹配组中的切片信道信息,反馈量大大降低。
总而言之,本文所提策略的主要优势在于避免了循环迭代,降低了计算复杂度,采用比例公平的资源分配策略提高了频谱效率。本文仿真只对这两方面性能进行说明。
5 仿真及性能分析
假定10个UEs均匀分布于区域中,3个MVNOs向1个InP租用资源向UEs提供业务,各MVNOs能容纳的用户指标分别为3,3,4,InP的信道抽象成10个切片。切片到用户的信道包含大尺度衰落和小尺度衰落,大尺度衰落由d-2决定,10个UEs的损耗根据与基站的距离决定,假定其中4个的损耗为1,4个的损耗为0.1,另外2个的损耗为0.05。所有信道的小尺度衰落服从均值相等的Rayleigh衰落,每切片的等功率为1 W,功率分配时,总功率保持与平均功率时相等,不考虑信道的误比特率,信噪比为-20 dB,速率为单位带宽的速率,用户满意度中的参数s取4.5。为简化,假定每用户所需切片数dk为1,用户购买带宽的价格、MVNOs向用户出售带宽的价格、MVNOs向InPs购买功率的价格以及InPs向MVNOs出售功率的价格分别均匀分布于[4 8],[2 4],[3 7],[4 6]。图3比较了本文提出的低复杂度的两层独立匹配博弈结合比例公平资源分配策略与两层联合匹配博弈的系统和速率,可以看到,本文提出的策略远远高于文献[12]中的两层联合匹配博弈。

图3 频谱效率比较Fig.3 Comparison of the two spectrum efficiency
图4(其中,策略1为本文策略,策略2为两层联合匹配博弈)比较了本文策略与两层联合匹配博弈在价格相同、信道改变时的效益。可以看到,由于两层联合匹配博弈在上、下层博弈中可以耦合,即MVNOs在向UEs提供带宽时,同时考虑向InPs购买功率的成本,因此各部分效用稍高于本文策略。但从计算复杂度来说,上、下两层联合的匹配博弈,要达到循环稳定,百次左右迭代在所做仿真中占比大概2/10,多数需要更多次循环。本文策略不需循环,只在匹配博弈之后增加少量计算,通过切片选择和功率分配,实现用户与切片间的精确匹配并提高频谱效率,计算量和跟踪时延大大降低,结合图3的效率提高,说明本文策略性能优于两层联合匹配博弈。
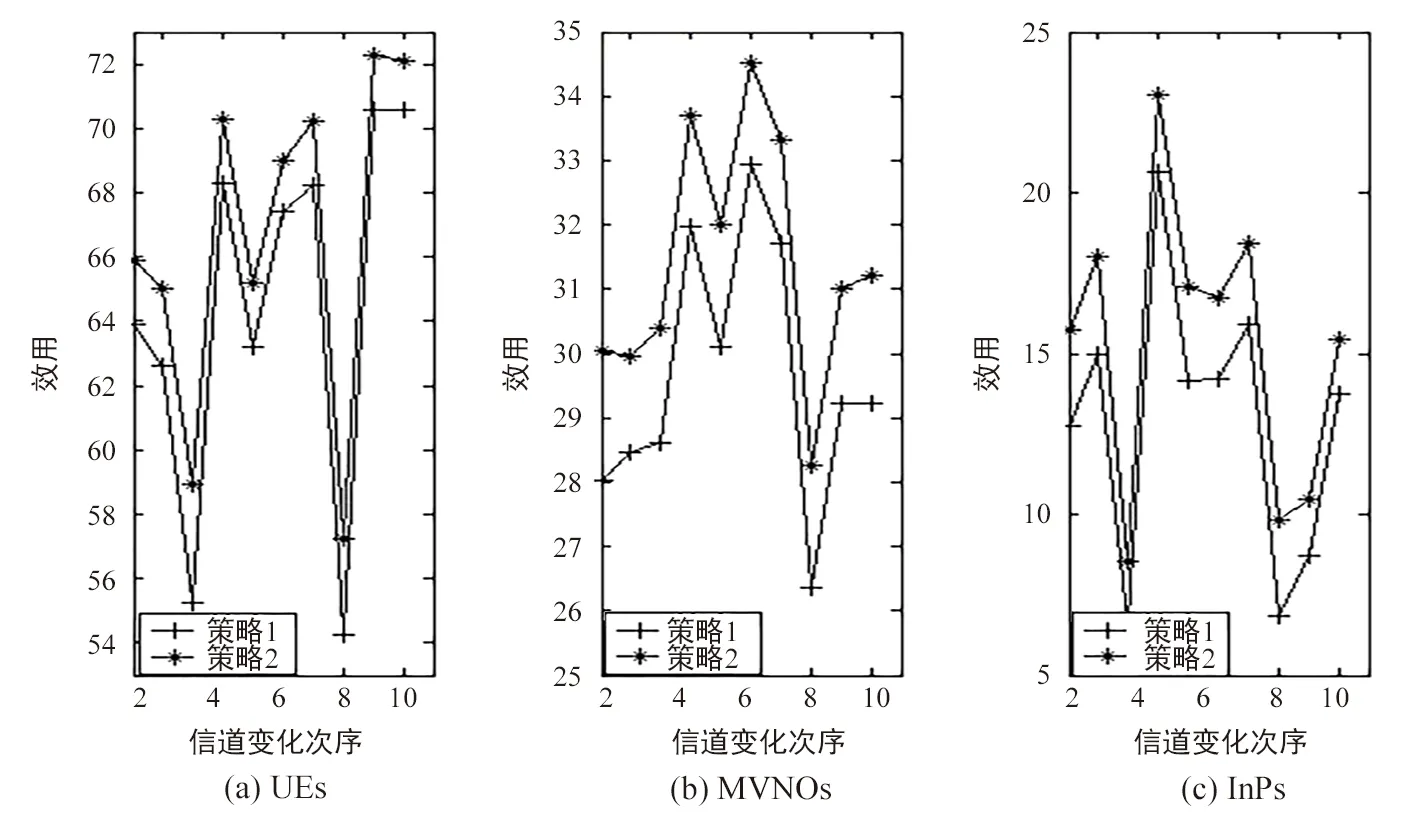
图4 效用比较Fig.4 Comparison of the two strategy’s utility
6 结束语
本文提出了一种低复杂度的分层匹配博弈结合比例公平的无线虚拟网络资源分配策略。通过两层独立的多对一匹配博弈实现用户组与切片组的匹配,在匹配的切片组与MVNOs间采用功率受限的比例公平资源分配策略,实现用户与切片的精确匹配,并在保证比例公平的条件下,使系统效率达到最大。仿真表明,相比两层联合匹配博弈,本文虽然效用稍低,但较大地降低了计算复杂度和跟踪时延,提高了频谱效率,总体性能更优。

