基于改进AHP算法的水利工程材料核心工序质量监控研究∗

（河海大学 南京 210000）

1 引言

对水利工程材料进行质量监控有着十分重要的生产意义和经济价值。对水利工程材料生产过程的把关和生产材料的质量也起着不可或缺作用［1～2］。在实际生产过程中，对品控的把握是以对核心工序把控作为基准点的，水利工程材料的生产需要经历几十个步骤环节，涉及到方方面面的生产准备、生产工艺以及生产的全过程，因此，如何选择和确定核心工序质量监控点是水利工程材料及其零部件生产加工过程质量监控的第一要务，也是先决条件［3～4］。所以首先需要对质量监控点进行科学合理地确定，工序质量监控工作才能做到有的放矢，才能有针对性地开展工序质量监控工作，确保最终生产出的水利工程材料能够符合品控把关的要求［5～6］。

2 改进的层次分析法（AHP）

有A、B、C三个矩阵，设A=［aij］、B=［bij］、C=［cij］∈Rn×n，根据定义，当aij=aij-1时，A为互反矩阵；当bij+bji=0时，B为反对称矩阵。

当A是互反矩阵时，且aij=aik/ajk，则A是一致矩阵，当B是反对称阵时，且同时满足bik+bkj=bij，则称B是传递矩阵［6～8］。

显而易见，若A是一致矩阵，则B=lgA（bij=lgaij，∀i、j）就会是传递矩阵，相反当B是传递矩阵时，则A=10B（bij=lgaij，∀i、j）是一致矩阵［7］。

当然，假设如果存在一个传递矩阵C，能够使(cij-bij)2的和最小，那么就称C为B的最优传递阵矩阵［8］。

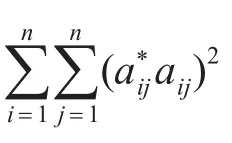
显然，若B是反对称阵，则B的最优传递阵C自然满足：

层次分析法（AHP）流程图如图1所示。

图1 AHP的流程图

改进的层次分析法（AHP）流程图如图2所示［10～11］。

通过图1和图2算法流程对比可得到，改进的层次分析法（AHP）省略了一致性检验步骤，简化了流程；另外，从构成C矩阵的公式中可以得知在改进的层次分析法（AHP）算法中会考虑各个指标之间的关系，特别是首先会分析各体个指标之间的关系，然后在分析任意两个指标与其他各个指标之间的关系的基础上再进行调整运算。由此可以得出，改进的层次分析法（AHP）是在分析完指标内在联系的基础后有一个再综合调整的过程，相对于一般的层次分析（AHP）算法，最显著的就是在于各指标之间调整过程上的改进［13～14］。

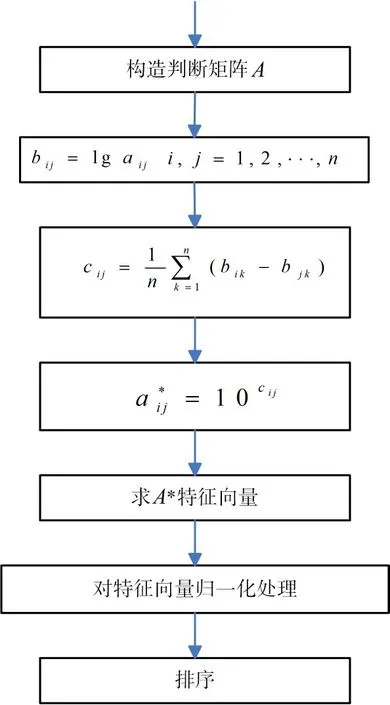
图2 改进的AHP的流程图

在利用改进的AHP算法建立核心工序质量监控决策模型之前，首先介绍以下几个概念。

1）核心工序：在生产过程当中有些工序具有加工难度大、质量不稳定、出现废品后经济损失较大、以及具有关键和重要特性等方面的特性，上述工序在产品质量的把关和经济成本的控制上处于关键位置一般称为核心工序［15～17］。

2）核心工序质量监控：在生产过程中为了确保产品质量，需要根据不同产品的特性以及生产该产品的方法步骤，来判断哪些环节和步骤对该产品的质量影响比较大，从而对这些生产环节和方法步骤进行从严控制，探索出该产品质量监控的核心点和通识性的规律［18］。

3）核心工序质量监控点：前面分析了产品质量与该产品的特性、生产环节和生产该产品的方法步骤等很多因素有关，要想很好地控制该产品的质量需要对这些影响因素进行分析，找出核心的工艺流程、产品特性等对产品质量影响最大的核心因素，对这些核心影响因素进行重点监控，以便实现对产品质量的控制，控制经济成本［19］。

3 质量监控决策模型

1）建立结构模型

水利工程材料的质量主要取决于生产过程，最为重要的是核心工序流程操作是否符合规范、是否符合标准，能够检验核心工序是否达到标准的方法和手段体现在该工序生产出产品的厚度、尺寸大小以及安装位置是否符合标准，公差有多少。实际上就是该道工序完成后上述三种标准的公差是否在一定的可接受的范围内，从而实现对核心工序的控制，建立的结构模型如图3所示［20～21］。

图3 水利工程材料工序质量控制点层次结构模型

根据前文对水利工程材料产品质量影响因素的分析可知，控制产品质量的核心在于对核心工序进行监控，实际上是对于确定的核心工序质量控制点进行监控，根据对于核心工序质量控制点定义的理解，结合建立的结构模型，可以设定评价集合为L=（l1，l2，l3，l4）=（水利工程材料特性的工序，工艺水平高的工序，故障率高的工序，生产成本大的工序）［22］。

2）构造判断矩阵

为了表示本层级与下一层级因素之间的影响力大小，也就是两者之间的相对重要性，构建判断矩阵Ak，下层因素集用Bk（k=1…n）如表1所示［23］。

表1 判断矩阵

其中，bij是对于Ak而言，Bi对Bj的相对重要性的数值表示，一般采用1，2，3，…，9及它们的倒数来得到bij，其中：

bij=1，表示Bi比Bj一样重要；

bij=3，表示Bi比Bj重要一点（稍微重要）；

bij=5，表示Bi比Bj重要（明显重要）；

bij=7，表示Bi比Bj重要得多（强烈重要）；

bij=9，表示Bi比Bj极端重要（绝对重要）。

bij的值取2，4，6，8时表示处于1，3，5，7，9两级之间的中间状态。

根据上述bij的赋值方法可知，判断矩阵满足：

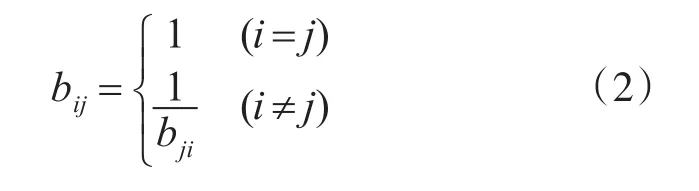
为了克服打分过程中，人为因素的影响，可对bij（相对重要性的数值表示）先期进行数据处理，转换计算如式（3）所示：

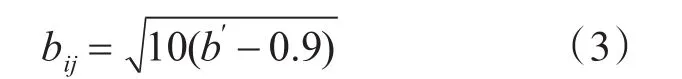
其中，bij，b′分别表示之前的的标度和处理后的标度，利用数据处理后的b′可以提高在判断过程中的客观性［15］。同时，还是为了保证专家在打分过程中的客观性，减少降低人为的主观影响，可以在评价判断过程中使用测定法。

通过以上分析，在实际计算过程中可以分别构建目标层和准则层的判断矩阵，用A和D来表示，具体见式（4）和式（5）。 准则层判断矩阵Dk(k=1,2,3)对应着厚度公差、形状大小公差以及安装位置公差［13］。

依据矩阵A，得到B=lgA：

4 实例分析

为了验证上述模型和计算方法，选取常用的水利工程材料密封闸阀组件为例进行实例分析，确定密封闸阀组件阀轴填料、阀杆和阀体的加工工序中为研究对象，构造判断矩阵。

由式（6）得：

分别得到C1、C2、C3、C 矩阵和相应的 A1*、A2*、A3*、A*矩阵如下：

对于有正规化权向量得：

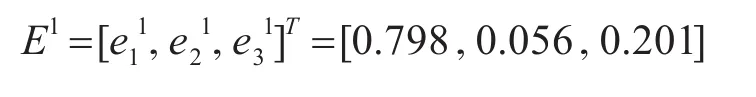
同理可求出：矩阵的权向量为

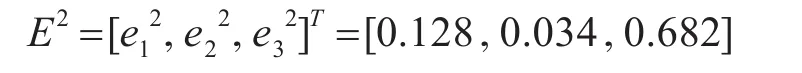
矩阵的权向量为

5 结语

在水利工程材料的生产和工程使用中，由于量产的规模化不断扩大，生产设备的不断更新换代，新生产技术和操作流程的不断应用，水利工程材料逐渐呈现出品种多样化的趋势，同时这也对产品质量提出了更高的要求。因此，对水利工程材料生产过程进行有效的监控显得十分的重要和十分的必要。有效的质量监控更能够确保所生产产品的合格率，并能够有效地降低在后期使用过程当中的各类风险因素，也能够大大节约经济成本。通过分析和研究水利工程材料生产过程，有效地对生产流程中的核心工序进行重点监控，既能够保证生产产品的质量又能够有效地控制监控过程中的工作量，很好地实现有的放矢。通过算法分析和构建基于改进的层次分析法（AHP）的核心工序质量监控模型能够有效的实现上述要求，为水利工程材料生产过程中的质量监控提供有效的决策依据。