基于弹目关系的多尺度跟踪方法研究∗

石胜斌 陈 栋 胡子阳 雷 鸣

（1.陆军炮兵防空兵学院高过载弹药制导控制与信息感知实验室 合肥 230031）

（2.陆军炮兵防空兵学院研究生大队 合肥 230031）

1 引言

目标跟踪技术在军事、医学、交通等领域有着非常广泛的应用，是计算机视觉领域重要的基础性研究课题之一［1～2］。近十几年来，无模型目标跟踪技术虽取得了较大进展，但由于目标图像受几何形变、光照变化、局部遮挡、快速运动等问题的影响，使得无模型目标跟踪仍是一个难题［3］。近几年，相关滤波方法［4～5］被引入视觉跟踪领域，并就跟踪过程中存在的常见问题对算法做出了相应调整和改进，在实时性和鲁棒性方面都有着不错的效果。同时，由于相关滤波类算法原理简单，可操作性强，对特定目标作针对性调整可取得较为理想的效果。

在精确制导领域，目标跟踪技术作为关键一环，其性能的优劣直接影响了打击效果的好坏。导弹在接近目标的过程中，视场中目标的尺度是势必会发生变化［6～7］。传统相关滤波算法为单一尺度估计，在目标尺度发生变化时，跟踪误差会不断积累并最终导致跟踪失败。尺度自适应与多特征融合跟踪器（Scale-adaptive and Multi Feature Integration Tracker，SAMF）［8］和强判别性尺度空间跟踪器（Discriminative Scale Space Tracker，DSST）［9］是 目前基于相关滤波器的目标跟踪算法中，能够有效解决目标尺度变化问题的代表算法。DSST算法通过加入与位置滤波器独立的尺度滤波器，虽然跟踪效果有所提升，但该算法的计算量明显增加，无法满足弹载平台对于实时性的要求［10］。SAMF算法通过加入尺度池，既在确定目标区域时对初始目标做若干尺度的缩放，经相关滤波器得到最大响应值所对应的尺度即为此时目标尺度，虽然其鲁棒性不及DSST算法，但该算法原理简单，计算量小，能够满足实时性要求［11］。

本文基于SAMF算法，结合弹目运动关系，对尺度池参数的选取进行探究，通过对比实验分析，以找出能够有效解决弹载目标跟踪中的尺度变化问题，同时能兼顾实时性的要求。

2 SAMF算法

2.1 算法原理

SAMF算法是核化相关滤波器（High-Speed Tracking with Kernelized Correlation Filters，KCF）［12］的改进算法，该算法的贡献主要有两点：一是将单一HOG特征拓展为HOG+CN+Gary的多特征融合，主要方法如下：

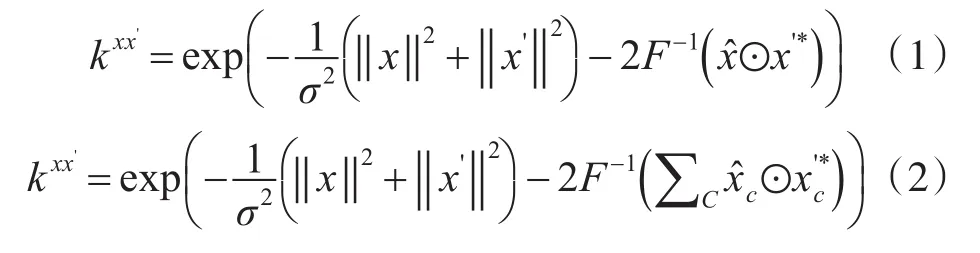
x是传统KCF算法中单一HOG特征，而xc中是三种特征的融合。算法相当于将三种特征进行简单的矢量叠加［13］。

图1 SAMF算法示意图

二是尺度的改进，由于KCF算法为单一尺度，当目标的尺度发生变化时会导致跟踪精度的下降。SAMF算法中引入尺度池的策略，论文中尺度池 为 Pools=｛0.985，0.99，0.995，1.0，1.005，1.01，1.015｝，既步长为0.005的7个尺度。其思想很简单，就是在确定目标区域时对初始目标做若干个尺度的缩放，经相关滤波器得到对应响应值，最大响应值所对应的尺度即为此时目标尺度。算法的示意图如图1。

2.2 跟踪效果

我们使用KCF算法和SAMF算法以及本文算法在同一视频序列上进行跟踪测试，目标为1：30坦克模型，利用无人机携带摄像头由高到低拍摄，实验结果如图2所示。

图2 跟踪效果图

由图2可知，三种算法均能基本锁定每帧中目标位置。由于KCF算法对应跟踪框没有随目标的尺度变化而变化，仅得到了目标部分纹理信息；SAMF算法虽有一定的尺度调整，但由于目标尺度变化较快，跟踪器的尺度估计跟不上目标的尺度变换，同样也仅得到部分纹理信息。而本文的改进算法具有较好的跟踪效果。

3 尺度池改进与结果分析

3.1 参数数目选择

SAMF算法中的尺度池包含7个尺度，参数的选取应兼顾跟踪器的精确度与实时性。尺度参数越多并不意味着精度越高，因为一旦发生偏差会导致误差积累，最终导致跟踪失败。本实验首先令尺度池参数步长不变，改变参数数目，如表1所示。

表1 尺度池选择

通过在OTB50［14］中具有尺度变化的数据集上进行测试，结果如下。

图3 OTB测试结果

由实验结果可知，当采用7个尺度时效果最好，不过3个尺度的跟踪精度虽降低了3%，但其跟踪速度却提升了70%，故本文采用3个尺度的SAMF算法。

3.2 弹目运动关系简化模型

本实验采用无人机摄像机模拟弹载摄像头，故将运动模型简化，假定无人机向目标区域的运动为匀速直线运动。示意图如图4所示。

图4 弹目运动关系示意图

设每帧目标尺度变化率为k，目标尺寸为S0，背景尺寸分别为S，S’则有：

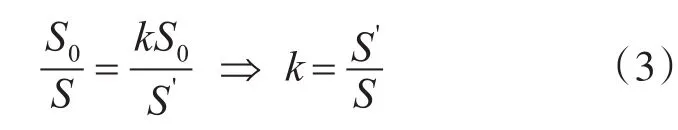
设无人机运动速度为v，初始高度为h，算法帧率为f，则在1s内：

无人机的运动速度v≈10m/s，起始高度h≈14m，帧率f=65fps由此可得：k≈1.02。故尺度池设定为｛1.00，1.01，1.02｝。

3.3 对比实验与分析

根据所得结果，我们将本文算法与单一尺度的KCF算法以及传统SAMF算法进行对比，通过计算三种算法的跟踪重叠率［15］，既计算预测框与标准框的重叠面积占标准框面积的百分比，以达到定量评估的目的，实验配置及运行环境为

名称CPU配置Core i5-7300HQ操作系统内存图像处理8G MATLAB2015、OpenCV3.1.1微软Windows 10

实验结果如图5所示。

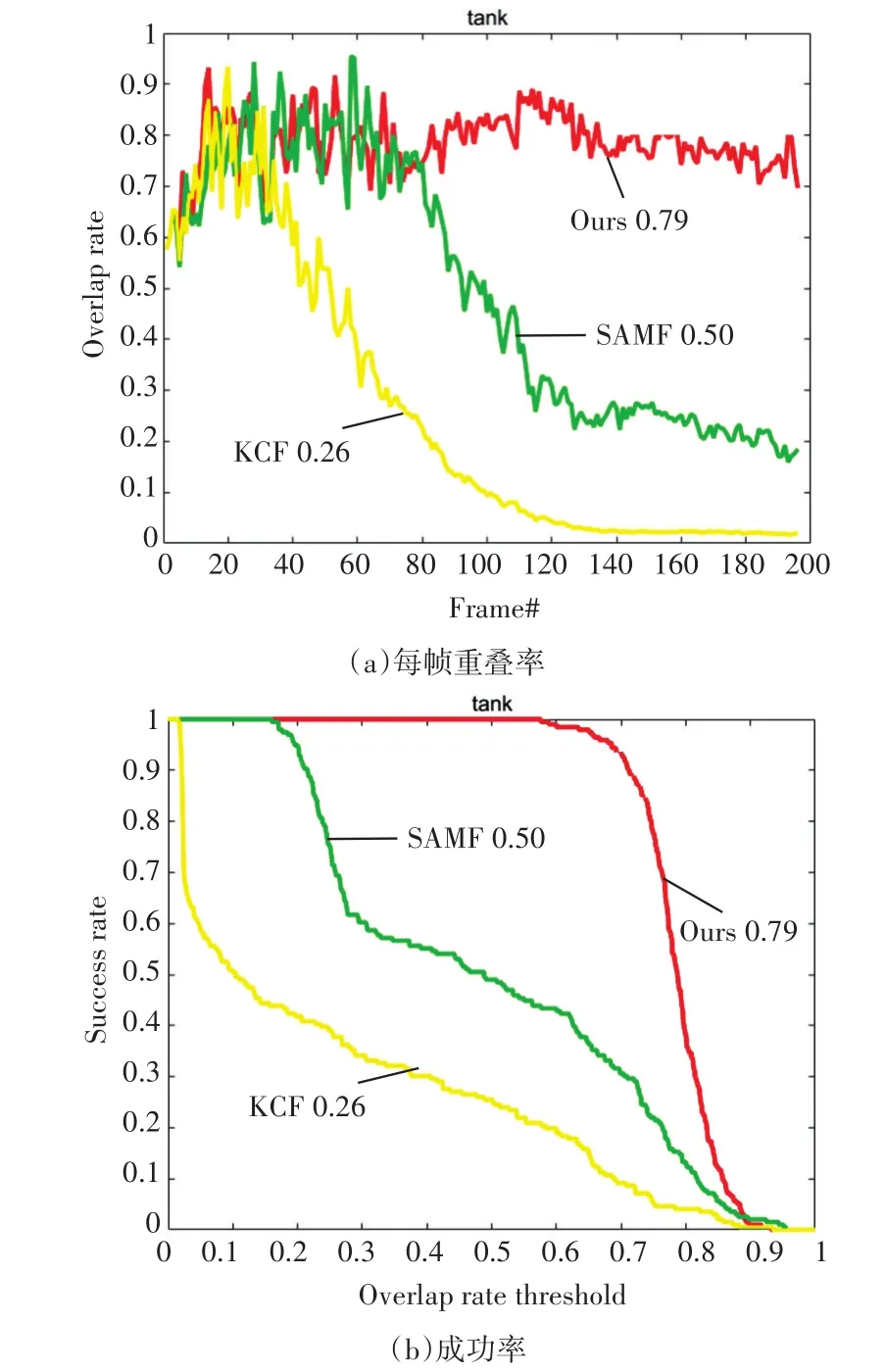
图5 三种算法重叠率

由实验结果可知，在弹目运动关系已知的前提下，针对特定的视频序列，本文算法精度较单一尺度的KCF算法提升了67.1%，较传统SAMF算法提升了36.7%，且能够满足实时性要求。

4 结语

本文针对弹载视频目标的尺度变化问题，在已知导弹与目标运动关系的前提下，通过对SAMF算法中尺度池的参数选取进行改进，使得其跟踪效果得到大幅提升，虽然本文的弹目运动关系模型较为简单，但本实验充分证明了该方法的可行性，为实现尺度自适应的弹载视频图像目标跟踪提供了新的思路。