考虑安装基座影响的光电平台等价捷联惯性稳定控制

王中石，田大鹏，石 磊，刘晶红

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2. 中国科学院大学，北京 100049；3.中国科学院 航空光学成像与测量重点实验室，吉林 长春 130033)

1 引 言

光电平台安装在飞机和舰船等运动载体上，为平台内部搭载的光电设备在惯性空间提供稳定指向，广泛应用在光电侦察、目标捕获与跟踪瞄准等领域。光电平台包含多个正交安装的机械转动框架，从外到内分别为外框架、中框架和内框架。通常将光电设备和提供控制反馈信号的陀螺仪安装在内框架中。陀螺仪直接测量光电设备在惯性空间中的角速度。通过控制驱动各框架转动的力矩电机，补偿载体姿态变化和环境干扰力矩的影响，实现稳定成像[1]。从控制方法的角度提升光电平台的稳定性能是提升光电装备整体性能的重要研究方向[2-3]。

现有研究大多是在陀螺直接反馈的基础上，从被控对象建模、扰动因素建模、内回路补偿与主动抗扰以及外回路控制算法等方面开展研究[4-6]。但是，在陀螺直接反馈的前提下，控制量来源于控制偏差。尽管能够实现稳态无偏差，但是在动态条件下，实际响应与给定指令之间的偏差从理论上即无法保持为零。因此，实际系统的控制精度、工作带宽都严重受到限制。

除将陀螺仪安装在内框架直接测量光电设备惯性角速度外，还可以将陀螺仪捷联安装在光电平台基座上，测量基座的姿态运动。文献[7]讨论了这种结构下的稳定控制，光电平台各轴的补偿指令等于测量的基座姿态运动量经坐标变换后的相反数，可实现间接惯性稳定，称为捷联惯性稳定。捷联惯性稳定方案直接敏感基座的运动，可以有效利用基座运动信息构造前馈环节，实现各轴对运动指令的完全跟踪，理论上控制误差为零[8-9]。文献[10]基于陀螺捷联安装的方式提出了一种自适应前馈控制方法，提高了惯性光电平台对控制指令的跟踪性能。与单纯的反馈控制系统相比，显著提高了系统的暂态性能。文献[11]针对捷联稳定的光电平台从动力学建模、摩擦补偿、微分测速、匹配滤波、控制系统设计等方面展开了详细的研究，全面提升捷联光电平台的稳定精度。以上文献研究的基础均建立在陀螺仪捷联安装结构之上。

此外，现有的研究针对光电平台进行建模分析时未考虑平台基座的动力学特性。实际上力矩电机驱动框架和载荷转动的同时，反作用力矩也会驱动基座转动[12-13]。若基座的转动惯量与电机转子和负载端的转动惯量相差不大，并且基座并未稳固安装于载体上时，捷联稳定方案会敏感基座的运动进而对整个控制回路构成影响[14]。为了在陀螺仪非捷联安装条件下实现等价的、动态误差为零的理想惯性稳定控制，解决轻质基座非稳固安装所带来的影响成为一个不可避免的问题。

本文建立了包含基座在内的光电平台控制系统模型，分析了载体对安装基座的弾性约束力矩对控制系统的影响。结合陀螺仪捷联稳定构建前馈的思想，设计了等价捷联惯性稳定控制方法。该方法基于考虑基座影响的完整模型设计了防止振荡的滤波器，在位置反馈层面构建干扰观测器进行内回路干扰补偿，利用光电平台框架相对位置转角以及安装在内框架的陀螺仪测量值在不改变光电平台结构的条件下，实现了带有前馈的等价捷联惯性稳定控制，理论上在低频工作范围内的动态误差为零。

2 建模与分析

2.1 光电平台基座和负载动力学建模

光电平台结构如图1所示，包括基座和负载两部分。

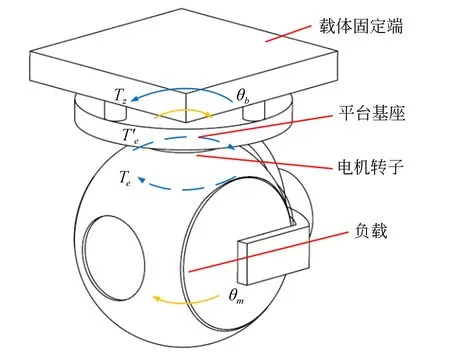
图1 光电平台结构示意图Fig.1 Schematic diagram of photoelectric platform

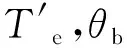
规定电机负载端转速方向为正方向，分别对电机负载和基座进行动力学建模，则有：

(1)

(2)

其中:Jm,Jb分别为电机负载端和基座端的等效转动惯量，Bm，Bb分别为电机负载端和基座端的等效阻尼。当基座转动惯量远大于电机负载转动惯量Jb≫Jm时，基座惯性角速度θb趋向于0，此时θb可以忽略。然而，当基座处于非稳固约束并且基座惯量并非远大于电机负载转动惯量时，θb则不可忽略。对θm和θb求和等效于电机转子和定子的相对转角，则有：

-θb+θm=θe.

(3)

在实际系统中，基座受到的约束力矩Tz十分复杂，可能包含弹性和非线性间隙等影响，难以对约束力矩进行完整建模。考虑到约束力矩主要由载机减振装置的弹性连接结构提供，将约束力矩Tz简化为弹簧模型：

Tz=Kb(θz-θb)，

(4)

其中:Kb为等效的弹性模量。对式(1)～式(4)进行拉普拉斯变换并整理得到由输入电磁转矩到基座转角的传递函数和由输入电磁转矩到框架相对转角的传递函数分别为：

(5)

(6)

根据式(5)和式(6)绘制包含基座和负载特性的光电平台被控对象模型框图，如图2所示。

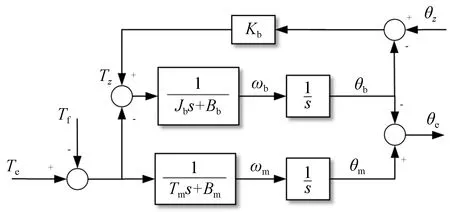
图2 光电平台被控对象原理框图Fig.2 Principle diagram for control of photoelectric platform

传统方法从ωm处直接通过安装陀螺仪获得反馈信号，因此，上述问题几乎不会影响到陀螺反馈控制系统。然而，当采用捷联稳定方法并且基座转动惯量与电机转子端转动惯量相当时，基座安装的影响就会显现。

2.2 谐振影响及分析

为直观了解基座动力学特性对于光电平台控制性能的影响，采用数值仿真法对光电平台速度闭环控制系统进行分析。速度环采用PI控制器，取Kp=1，Ki=5，被控对象负载参数设为Jm=0.001，Bm=0.01。基座与电机负载转动惯量比为k=Jb/Jm=1，基座约束力矩中的弹性模量Kb=10。仿真中采用“库伦+黏滞”摩擦模型：

(7)

式中:静摩擦系数Tc=0.5，黏滞摩擦系数b=0.3。输入幅值为0.159°、频率为1 Hz的正弦角度信号模拟载机运动，得到基座惯性角速度和编码器角速度曲线如图3所示。

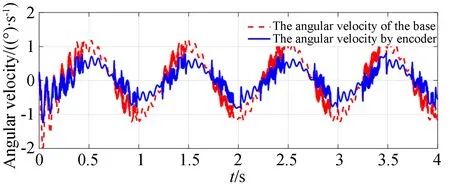
图3 载机正弦运动条件下系统角速度应曲线Fig.3 Angular velocity response curves for aircraft under sinusoidal motion

为了定量分析基座约束条件对控制系统频率特性的影响，对基座角速度信号的振动幅值做标量化处理并采用快速傅里叶变换分析，在选择不同Kb值时得到系统角速度响应的振动频率特性曲线，如图4所示。可见，输出角速度除了在1 Hz的工作频率有较高的幅值响应外，在更高的频率上出现了一定的谐振。随着弹性系数Kb逐渐变大，系统谐振频率越来越高，幅值越来越大。

数值分析说明基座与光电平台之间的连接刚度会影响光电平台的运动响应特性。非稳固、非刚性的连接会引入谐振特性。

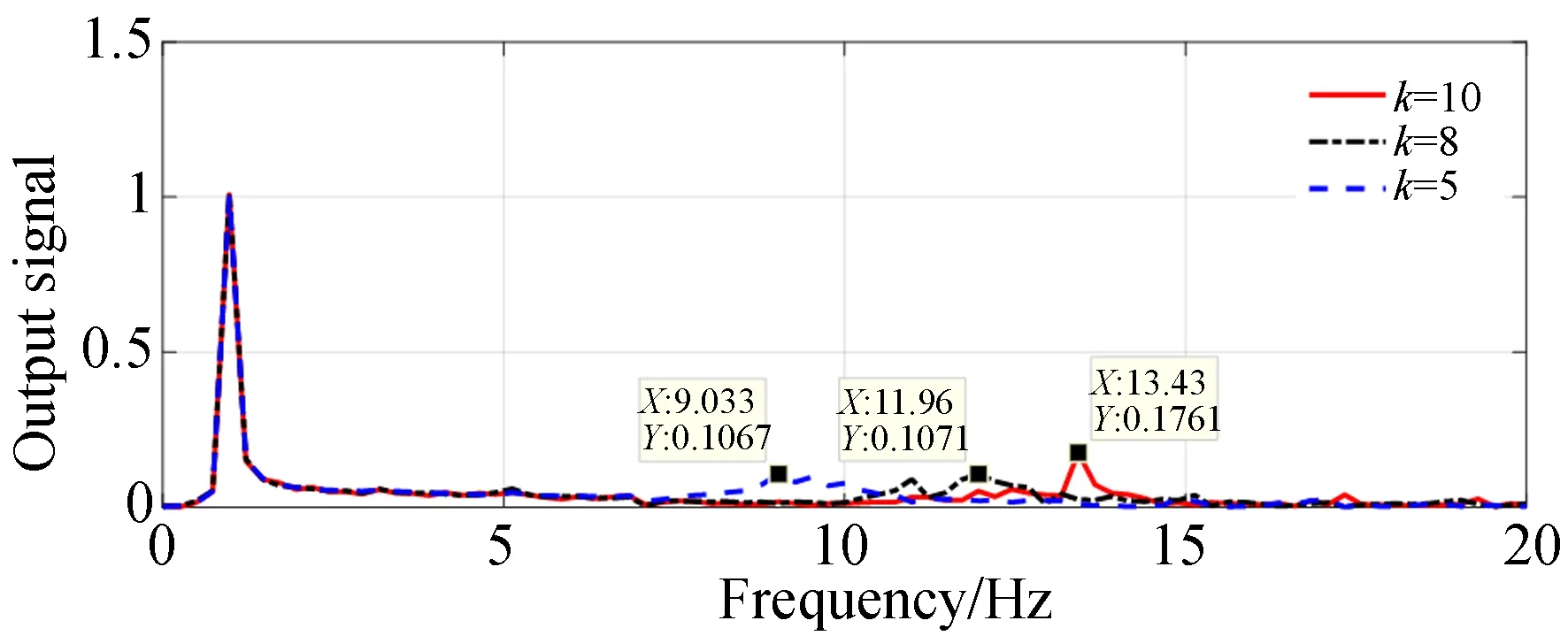
图4 弹性模量与谐振频率变化曲线Fig.4 Curves of elasticity modulus and resonance frequency

3 等价捷联惯性稳定复合控制

在考虑基座非刚性连接，陀螺安装在内框架上进行直接反馈测量的条件下，提出一种等价捷联惯性稳定复合控制方法，既保证系统稳定工作无谐振，又能等价实现陀螺捷联。该方法包括基于模型的滤波器、干扰观测器、等价捷联惯性稳定控制回路3部分。首先，针对基座弹性约束力矩影响导致被控对象中出现的一对谐振和反谐振环节，基于稳定的零极点对消设计消除谐振的滤波器，将被控对象的响应特性校正成受到等价干扰作用的名义模型。接着，基于DOB在内回路补偿等价干扰。最后，综合利用陀螺和编码器的反馈信号，设计逆模型前馈和双闭环反馈控制器实现等价捷联惯性稳定。控制原理框图如图5所示。

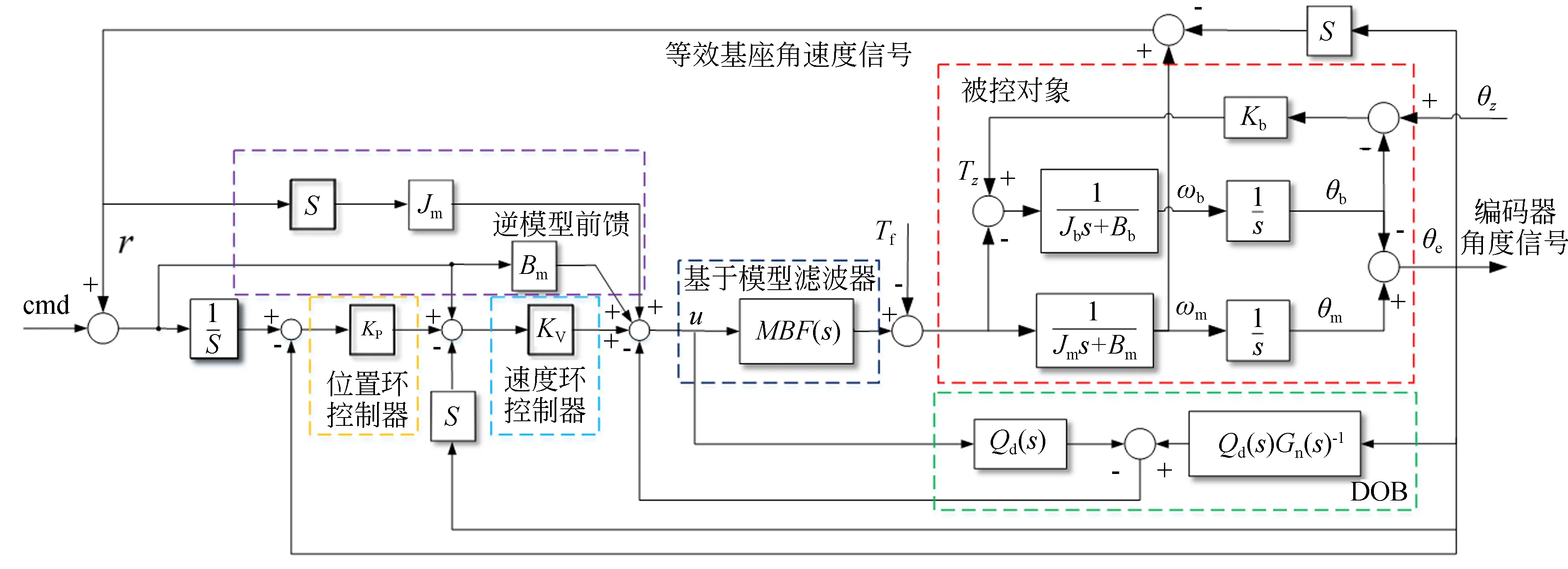
图5 等价捷联惯性稳定复合控制原理Fig.5 Schematic diagram of equivalent strapdown inertial stabilization compound control

3.1 基于模型分析的滤波器设计

根据式(6)可知，光电平台由于受到安装基座的影响，被控对象模型中会出现一对谐振和反谐振环节。本文提出基于模型分析设计滤波器的方法(Model-Based Filter, MBF)，从影响产生的机理设计滤波器，消除谐振频率处的控制力矩成分，提高反谐振处的系统增益，进而将基座非稳固安装条件下的光电平台动力学特性改造为接近名义模型的状态。基于模型分析设计的滤波器形式如下：

(8)

式(8)为具有稳定零极点的二阶环节。传统消除谐振的陷波器设计是通过辨识、拟合谐振的频率特性，采用一般性的双T网络设计，其参数的物理意义为振动频率和阻尼比[15]。而本文基于模型设计的滤波器，从问题产生的机理出发，滤波器的参数为等价惯量、等价阻尼、弹性模量等，具有明确的物理意义，可通过对光电平台结构进行有限元分析得到参数值。

3.2 基于DOB的内回路补偿

为了使被控对象更加逼近名义模型，采用干扰观测器(Disturbance Observer,DOB)将干扰力矩和模型不确定性等效为控制输入端的干扰，借助名义模型的逆模型和实际作用在被控对象的控制量估计出等价干扰并在控制量中引入等量的补偿，实现对等价干扰的抑制，其原理框图可见图5的DOB部分。

Gp(s)=Gn(s)(1+Δ(s))，

(9)

根据灵敏度函数定义可得到灵敏度函数：

(10)

在低频段时名义模型接近实际模型Gp(s)=Gn(s)，则补灵敏度函数T(s)为：

T(s)=1-S(s)=Qd(s)，

(11)

其中Qd(s)是低通滤波器。由小增益定理可知，加入DOB后系统鲁棒稳定的充分必要条件是[16]：

‖Δ(jw)T(jw)‖=‖Δ(jw)Qd(jw)‖≤1.

(12)

DOB的设计主要是在确定名义模型后调节Qd(s)的带宽以满足鲁棒稳定性要求。

3.3 等价捷联稳定的复合控制

利用编码器测量的框架相对运动角度微分得到角速度，再结合陀螺测量的惯性角速度可以计算出基座框架未安装陀螺部分的惯性角速度。即等价得到了陀螺捷联安装的测量值。利用这种折算，可以等价实现陀螺捷联稳定模式，并构建带有前馈的复合控制回路，提高惯性稳定控制的带宽。复合控制由反馈环节和前馈环节组成，有：

(R(s)-θe(s)s)Kv+R(s)(Jms+Bm)，

(13)

其中:Kp和Kv分别为位置环增益和速度环增益,R(s)/s为基座惯性角度信息，θe(s)s为编码器角度经过微分后的角速度信号。

反馈控制取编码器作为反馈信号，控制的是机械框架的相对角运动,其指令为基座惯性角速度的相反数，即控制框架运动实现对基座惯性姿态运动的反向最终从而使平台实现惯性稳定。而前馈则利用式(3)等价计算得到的基座惯性角速度构成，基于编码器闭环控制对象的名义模型构建前馈。

在加入DOB进行内回路补偿后，对于外环控制器而言，被控对象的特性近似于名义模型Gn(s)。前馈控制器为C2(s)，反馈控制器为C1(s)，输入角度指令为R(s)/s，输出反馈角度为θe(s)。

由于前馈环节并不影响控制系统的稳定性，因此，在根据式(12)设计DOB滤波器的前提下，控制系统的稳定性只取决于双闭环反馈环节的增益Kp和Kv。针对名义模型引入双闭环反馈后控制系统的特征方程为：

Jms2+(Kv+Bm)s+KpKv=0，

(14)

可见只要保证Kp和Kv均>0，即可保证控制系统的稳定性。在实现惯性稳定时，利用前馈控制可以提高动态性能，保证机械框架相对转动角度完全补偿掉基座的惯性角度变化，前馈的设计目标是使利用编码器测量的角度闭环反馈控制回路的闭环传递函数接近1，实现完全跟踪[17]，则有：

Φ(s)=θe(s)s/R(s)=1.

(15)

系统的闭环传递函数为：

(16)

则可得到前馈环节取名义模型的逆模型C2(s)=Gn-1(s)时，系统闭环传递函数Φ(s)恒等于1。

前馈控制C2(s)=Jms+Bm器 ，其中加速度信号需要通过速度信号进行微分得到。为避免噪声的影响，采用文献[18]提出的非线性跟踪微分器实现微分计算。

4 仿真分析

采用MATLAB进行仿真分析，被控对象负载端模型参数Jm=0.001，Bm=0.04，模型包含10%的不确定性，基座模型参数Jb=0.01，Bb=0.04，摩擦参数Tc=0.1，b=0.5，基座弹性力矩系数Kb=10。

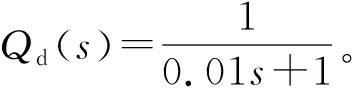
为了验证本文控制方法的有效性，引入陀螺直接反馈控制作为对比。输入幅值为1 (°)/s、频率为1 Hz的正弦角速度信号，绘制系统响应曲线和角速度误差曲线，如图 6所示。仿真结果表明：本文提出的控制方法与陀螺反馈控制相比，在受到摩擦干扰时，角速度误差可以较快地收敛，并且角速度均方根误差由0.032 (°)/s减小到0.009 2 (°)/s。

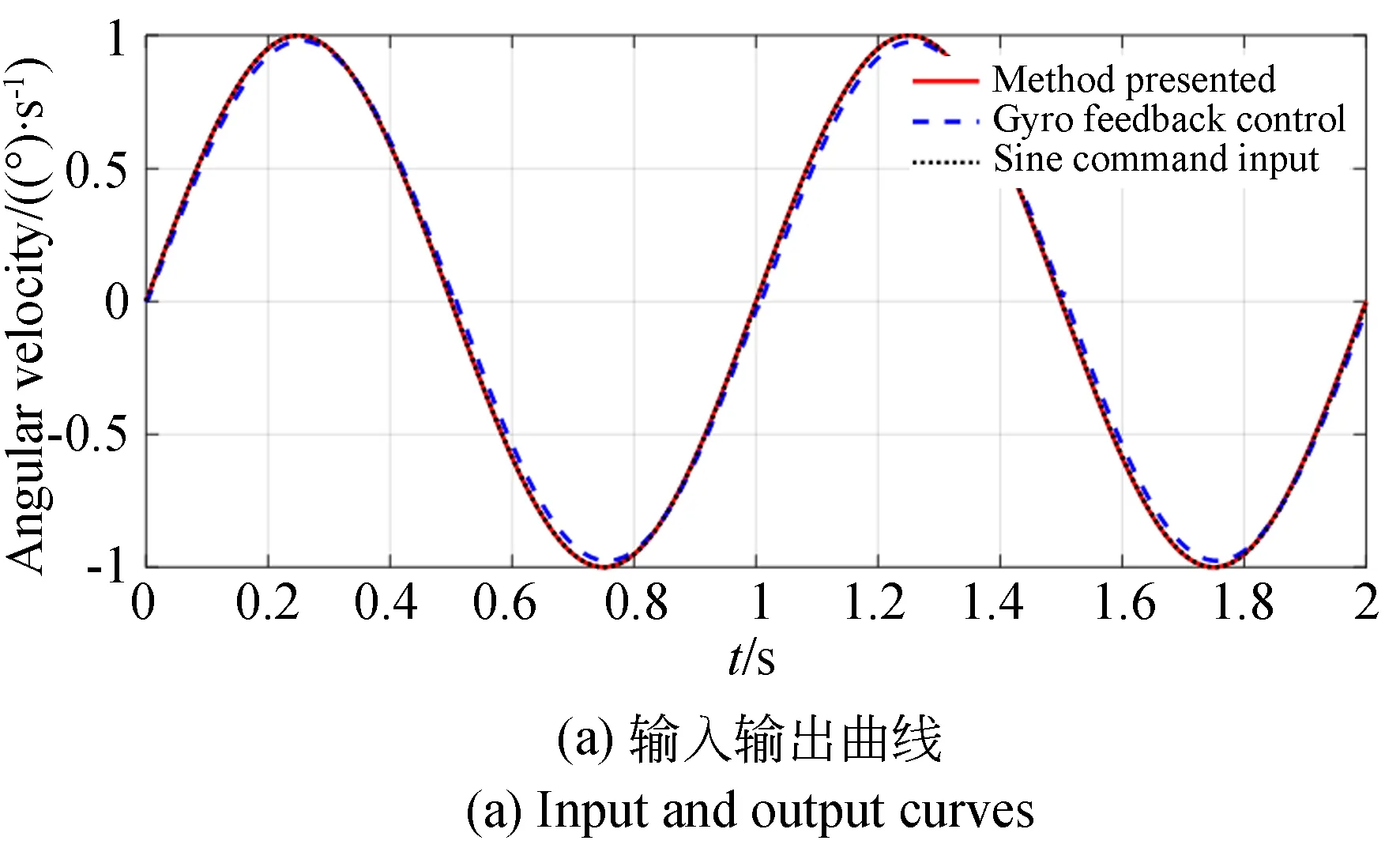
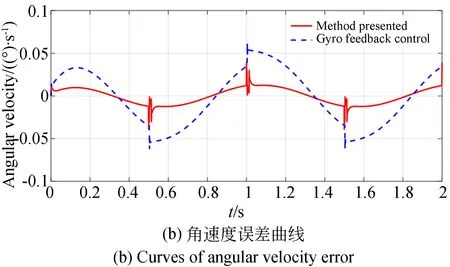
图6 陀螺反馈控制和等价捷联稳定复合控制方法对比仿真曲线Fig.6 Simulation curves of gyro feedback control and equivalent strapdown stability compound control

5 实验测试与结果分析

5.1 实验设置

为验证本文方法对光电平台控制系统性能的改善效果，搭建了单自由度实验装置。系统硬件由带编码器的力矩电机、基座、负载盘、陀螺、控制电路板和电源组成，如图7所示。

图7 光电平台实验系统Fig.7 Photoelectric platform experimental system

5.2 实验结果

实验平台基座采用非稳固连接方式与固定框架连接，模拟光电平台非稳固的基座安装影响。首先，根据实验装置结构有限元分析得到基座的等效弹性模量、等效转动惯量和等效阻尼参数值，以此为依据设计消除谐振的滤波器。为了验证上述滤波器效果，采用伪随机噪声对光电平台系统再加入滤波器前后分别进行噪声扫频，对被控对象进行模型辨识，绘制系统Bode图，如图 8所示。

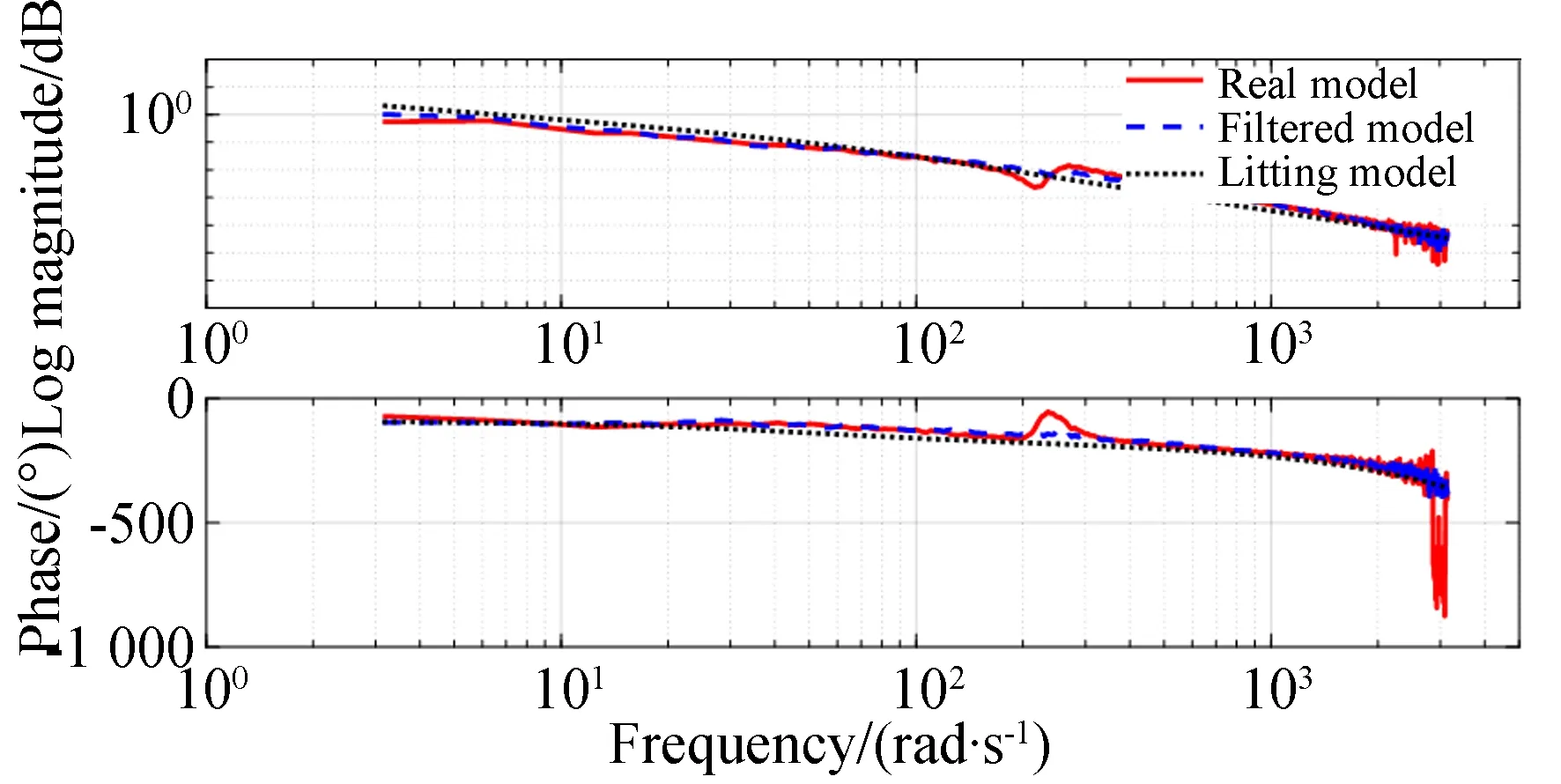
图8 实际模型、滤波后模型和拟合模型的幅频特性曲线Fig.8 Amplitude-frequency curves of real model, filtered model and fitting model

基于模型滤波器的设计参数如下：

(17)

加入滤波器后的名义模型为：

(18)

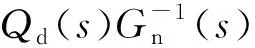
(19)

调节控制系统速度环增益，原则上在保证系统不发散的条件下尽量增大，同理整定位置环增益。最后，根据名义模型加入逆模型前馈 ，实现本文的等价捷联惯性稳定控制。

实验分为两组：正弦输入的时域实验和隔离度测试的频域实验。为了方便研究载体在宽频带运动时光电平台的惯性稳定性能，引入频率隔离度的概念[19-20]。针对本实验系统，频率隔离度是系统在惯性稳定工作时，根据电机负载端惯性角速度信号和基座施加干扰的惯性角速度信号，绘制幅频特性曲线。对比组实验采用陀螺直接反馈控制。

根据某工程项目要求，设计输入幅值为10 (°)/s、频率为1 Hz的正弦信号，记录输入和输出角速度信号，响应曲线如图9所示。与传统方法相比，新方法指令的动态跟踪性能更优。角速度跟踪误差的均方根值为0.23 (°)/s，而陀螺反馈控制的角速度跟踪误差的均方根值为1.75 (°)/s。本文方法有效提升了控制系统的动态性能，并且没有发生明显的谐振。

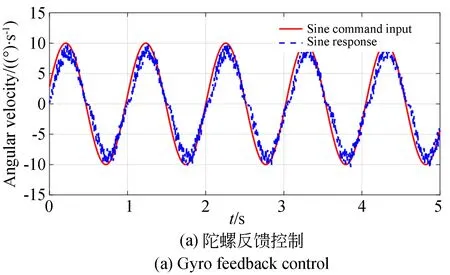
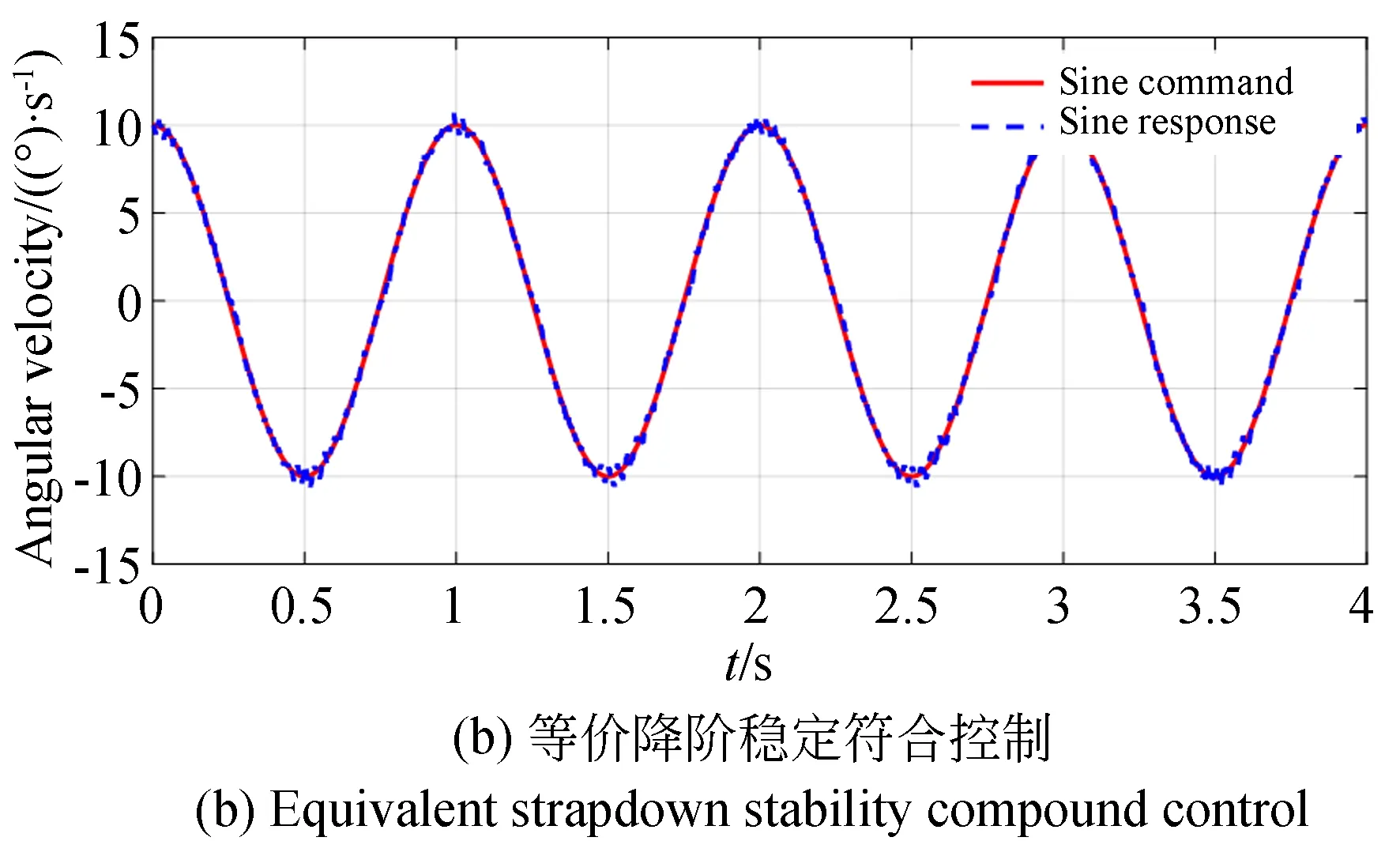
图9 两种方法的正弦输入指令和响应曲线Fig.9 Sinusoidal input and response curves of two methods

在实验平台上测试本文方法的频率隔离度指标，验证本方法对扰动的隔离能力。令载体进行反复多次的摇摆运动，采集载体惯性角速度和电机负载端的惯性角速度信号，绘制从载体惯性角速度到稳定后框架惯性角速度的幅频特性曲线并比较两种控制方法，结果如图 10所示。

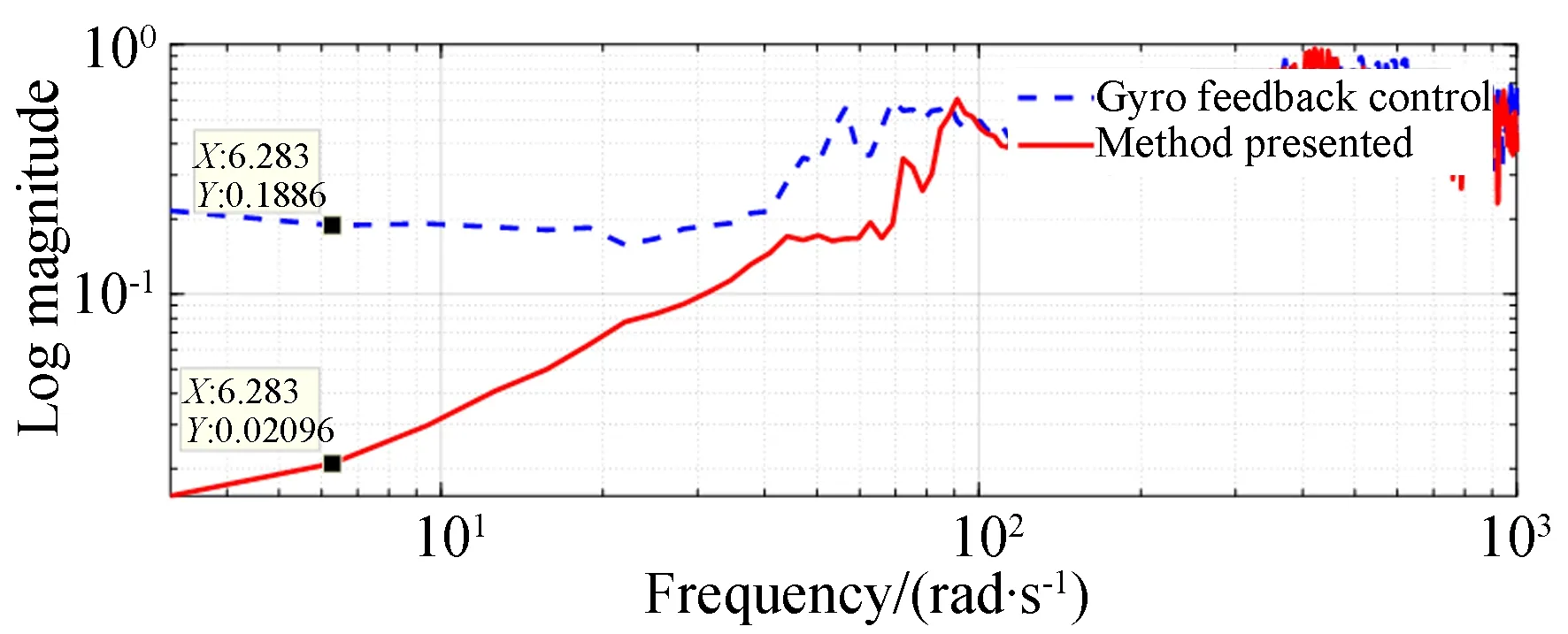
图10 陀螺反馈控制和本文方法的隔离度曲线Fig.10 Isolation curves of gyro feedback control and proposed method

由图10可见，本文方法的隔离度优于传统陀螺反馈控制方法。这意味着，本文方法对外界的低频扰动的隔离效果更好，取典型频率1 Hz处的隔离度进行定量比较，陀螺反馈控制的隔离度为18.9%，而本文方法的隔离度为2.1%。

6 结 论

本文提出了在陀螺直接反馈的机械安装条件下实现高性能等价陀螺捷联稳定的控制方法。考虑基座的安装条件，建立了包含基座和负载两部分的光电平台动力学新模型，并发现安装刚度会引起谐振的问题，由此提出了基于模型消除谐振的滤波器设计方法。该方法有效提升了光电平台的控制性能。对该方法进行了仿真和实验，结果表明，与传统陀螺直接反馈控制相比，在不改变现有光电平台陀螺的安装条件下，新方法使平台对指令的跟踪性能以及对姿态晃动的隔离性能均有明显提升，具有重要的工程实用价值。