高速列车气动噪声源强及分布特性数值仿真分析

柳润东，何财松，李晏良

（中国铁道科学研究院集团有限公司 节能环保劳卫研究所，北京 100081）

0 引言

随着列车运行速度的提高，高速铁路的噪声水平会显著增加。气动噪声是由列车高速运行时车体表面结构不平顺与空气相互作用产生的噪声，是高速铁路噪声的主要组成部分，在列车更高速度下将成为最主要噪声源。

国外学者对气动噪声的研究方法、声源特性及远场传播特性开展了研究。THOMPSON D J 等[1]总结了国外列车气动噪声的研究方法，主要有风洞试验、声源识别阵列、数值模拟等方法，并对气动噪声的控制措施进行了回顾；POISSON F[2]对世界上不同系统高速列车气动噪声进行了回顾，分析了降噪措施及效果；MASSON E等[3]对TGV高速列车气动噪声数值预测方法进行了研究，认为整流罩可有效降低列车气动噪声；MITSUMOJI T[4]等通过使用CFD (计算流体力学)方法研究采用等离子体激励器来降低受电弓弓头气动噪声。

国内学者同样对气动噪声进行了大量研究，郝南松[5]以某航空声学风洞为平台，研究了高速列车气动噪声风洞试验技术，并对某具体车型开展风洞试验，认为转向架区域气动噪声主要集中在中低频，受电弓区域气动噪声主要集中在中高频；高阳等[6]对CRH3和CRH380C 型车开展气动噪声风洞试验对比分析，认为改善后的转向架结构明显降低了列车气动噪声；姜世杰等[7]对高速列车车头气动噪声进行了仿真与试验研究，并对结果进行了对比分析；崔健等[8]通过仿真与实测对列车远场气动噪声进行了研究，认为远场气动噪声同样分布在较宽频带；张亚东等[9-10]对整车气动噪声声源特性及降噪措施进行了研究，认为整车气动噪声能量主要分布在4 000 Hz以内，对受电弓气动噪声进行了单独模拟，认为采用开口方式运行可有效降低气动噪声；朱剑月等[11]对转向架区域的流场及气动噪声进行了研究，认为安装裙板可在较宽的频段内降低转向架区域的气动噪声；孙振旭等[12]对国内高速列车气动噪声的研究现状进行了系统总结，包括气动噪声的主流研究方法及结论，并讨论了未来可能的研究方向。本文采用气动噪声数值模拟混合求解方法，对高速列车气动噪声的源强及分布特性开展数值仿真分析，并根据流场结构讨论了各部位气动噪声的产生机理。

1 计算模型与计算方法

1.1 气动噪声计算方法

目前关于气动噪声的计算方法主要有2 种，一种是直接噪声模拟方法(Direct Noise Computation，DNC)；第二种是混合求解方法。由于声场量与流场量存在尺度和能量上的巨大差异，直接求解方法需要采用高阶精度、低耗散、低色散的离散格式来提高求解精度，这给外形复杂、部件众多的高速列车气动噪声计算带来困难，并不适合工程应用。目前工程领域主要采用混合求解方法，该方法分为2 个步骤，即声源模拟和声传播求解，首先通过CFD计算获得流场信息，再通过Lighthill 基本方程将近场流动构造出气动声源，之后利用FW-H 声比拟积分法进行声场传播求解。在此，采用CFD与声比拟积分法相结合的混合求解方法。气动声学基本控制方程Lighthill公式如(1)式所示。

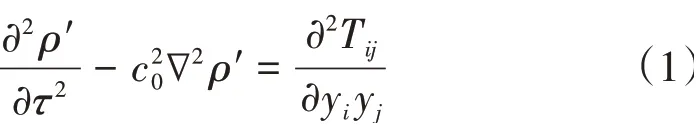
式中：Tij为Lighthill 张量为单位张量；eij为粘性应力张量，eij=为空气密度，ρ'为密度波动量，ρ'=ρ-ρ0；p0为流场压力初值，p'为流场压力脉动量，p'=p-p0；c0为声速。

FW-H方程如(2)式所示。

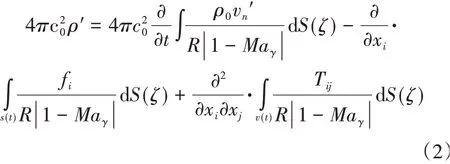
式中：R=|x-y|，x为接受点位置，y为声源点位置；Maγ为运动马赫数在观察方向上的投影；fi为静止固体边界的单位法向量。

1.2 计算模型与边界条件

按1:1 尺寸建立某型号动车组车体、受电弓及转向架区域几何模型，对受电弓和转向架构件进行了适当简化；计算域尺寸为600 m×80 m×40 m；计算网格采用切割体网格，在受电弓及转向架区域进行了网格加密，网格总量约300万；流体计算采用DES分离涡模拟方法，k-ω湍流模型进行计算，并引入嵌套网格方法，分别做出列车域及背景域网格；在列车运动路线上进行网格加密，模拟列车以不同速度行驶时的绝对运动。计算域、几何模型及网格划分如图1所示。

1.3 计算工况及验证

计算动车组列车分别以250 km/h、275 km/h、300 km/h、325 km/h、350 km/h、375 km/h和400 km/h速度运行等7 组工况，并以300 km/h 工况为标准进行网格无关性验证，对比加密后的网格计算结果，证明与网格尺度无关。根据文献[5]中风洞试验结果的数据对本文计算结果进行验证，误差在1.5 dB以内，证明了计算结果的准确性。

2 计算结果及分析

2.1 高速列车气动噪声源强特性

高速列车气动噪声，主要由空气与结构相互作用产生明显流动分离，之后由湍流结构发展及流体与壁面摩擦撞击产生气动发声。首先提取头车转向架及受电弓区域的涡结构分布图，如图2和图3所示。

图1 计算域、几何模型及网格划分

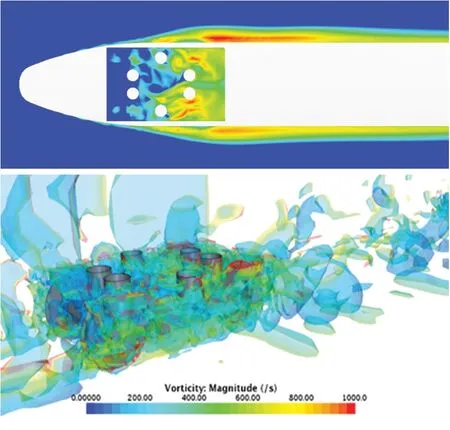
图2 头车转向架区域涡结构

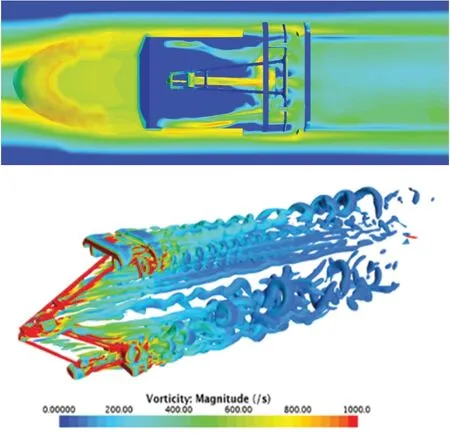
图3 受电弓区域涡结构

由图2 可知，转向架区域结构复杂，气流高速流经转向架舱时，直接撞击到转向架上，并在舱内散射，第一转向架舱内的气流湍化程度最高，产生的气动噪声也最大，同时由于转向架舱壁的约束，在此处并未形成有规律的涡旋，并且各涡结构差异较大。由图3 可知，受电弓存在的杆件结构在列车高速运行时引发周期性的涡脱落，涡脱落在杆件上产生周期性的作用力，形成较强的偶极子声源，产生以涡脱落频率为峰值主频的气动噪声。

Curle声功率模型可以表示偶极子声源的声功率表面分布特性，采用该模型对比了高速列车不同区域表面声功率分布，并以350 km/h速度级为例，提取结构表面声功率分布图(见图4)，并提取出各速度级下列车不同区域结构表面最大声功率级值，如图5所示。

由图4 可知，头车表面声功率级大于其他车，在车头流线型过渡区段，声功率变化更为剧烈；受电弓结构表面弓头附近声功率级最大；在同一速度级下，不同位置处的转向架气动噪声差别较大，头车前转向架的声功率级大于其他区域，并且不同位置处转向架表面声功率级均为后半部分大于前半部分。

由图5 可知，列车表面各区域声功率级随速度增高而显著增大，同时由文献[9]可知，气动噪声最大声功率级Pm与列车运行速度关系可表示为

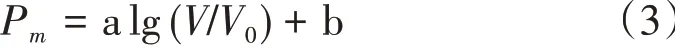
式中：V0为参考速度，取V0= 200 km/h；V为列车计算速度；a、b为需要确定的常数。

通过对计算结果进行数值拟合，可得到头车、受电弓、头车前转向架等不同区域最大声功率级与列车运行速度之间的函数关系，如(4)式～(6)式所示，拟合结果相关系数分别为0.996、0.994和0.998。

头车区域气动噪声拟合函数为

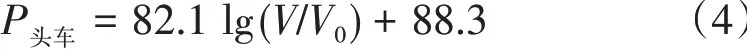
受电弓区域气动噪声拟合函数为

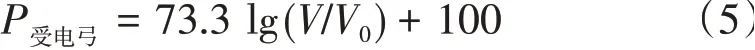
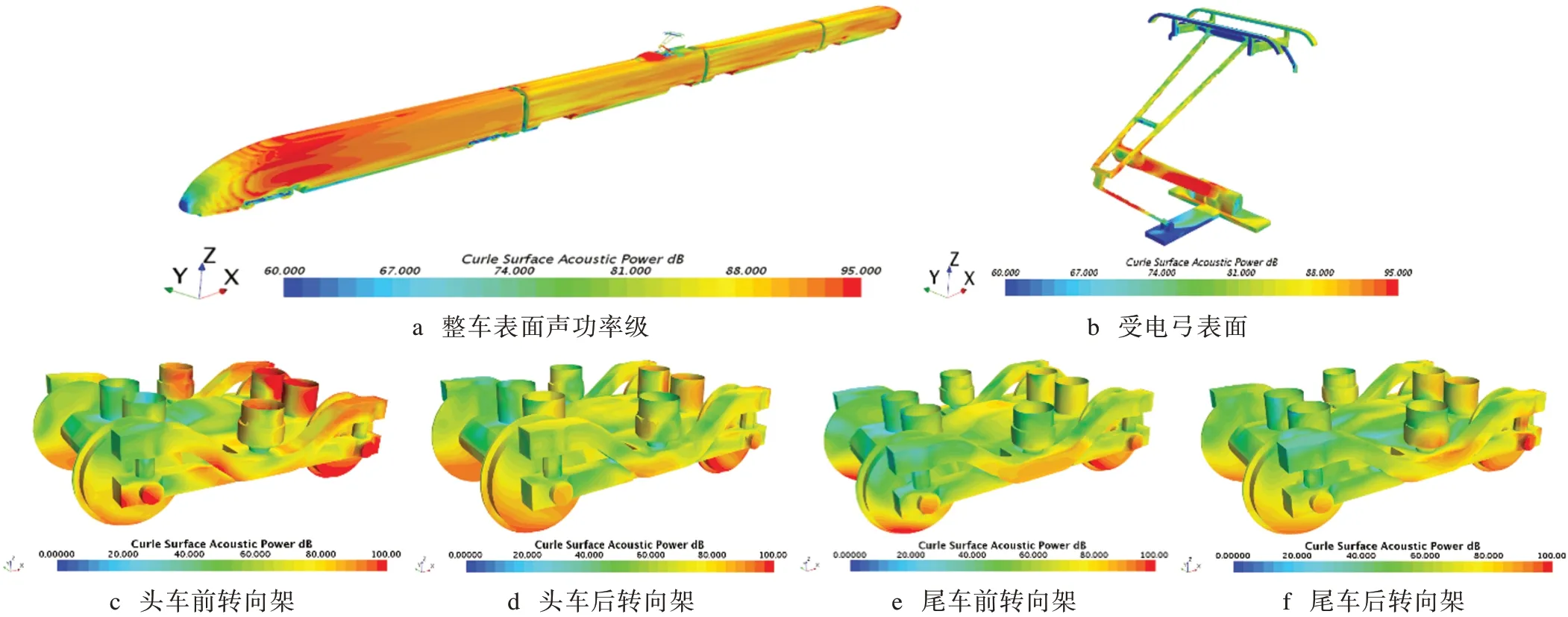
图4 高速列车不同区域结构表面声功率级分布

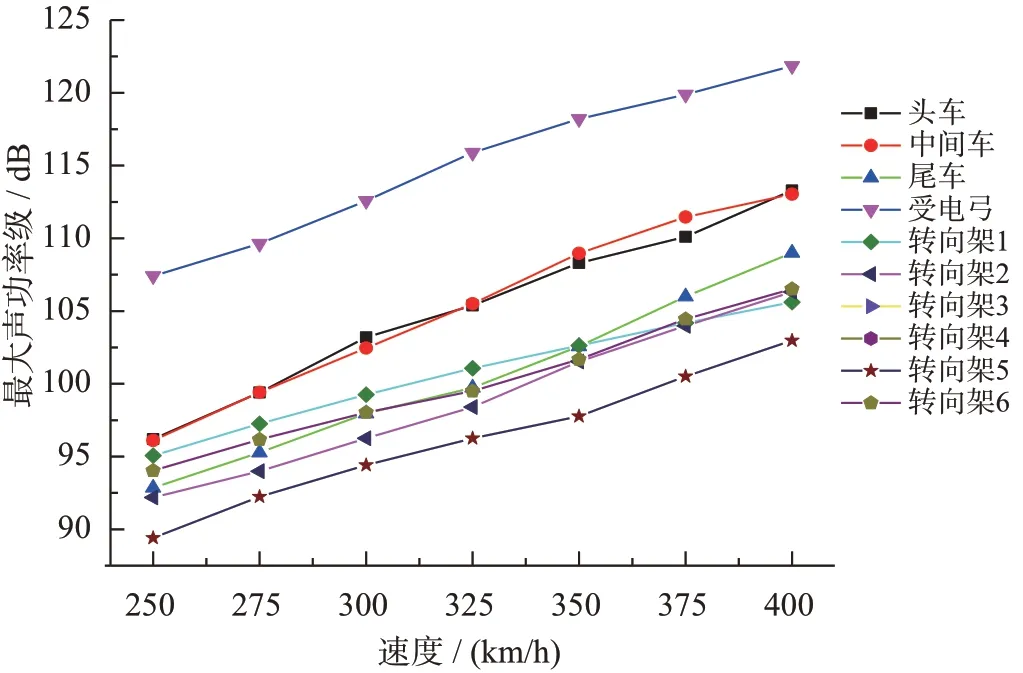
图5 不同速度下列车各区域最大声功率级

头车前转向架区域气动噪声拟合函数为

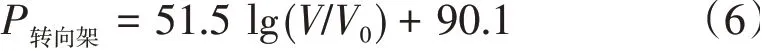
2.2 高速列车气动噪声源近场分布特性

选取头车、受电弓车及尾车为研究对象，分别在距线路中心线5 m、10 m 和15m，高度均为1 m 位置处设置了监测点，如图6(a)所示，利用FW-H 声比拟模型计算得到了测点位置处的声压级频谱特性，如图6(b)～图6(d)所示。

由图6 可知，空间中监测点气动噪声频率主要集中在100 Hz 以下的低频区域，同时在400 Hz 左右出现了增高；头车的声压级最高，其次为受电弓车，尾车的声压级最小；随着监测点距车体距离的增加，3 个测点处的声压级均明显降低，其中头车降低幅度最大。

3 结论

（1）列车高速运行时，车体表面由于与气体的摩擦效应形成偶极子声源，同时在列车附近形成较为强烈的湍流，并向远场辐射；随着速度级的提升，列车表面声功率级明显增大，在车头车尾、转向架区域、受电弓区域变化则更为剧烈。

（2）由于转向架舱壁的约束，转向架舱区域未形成有规律的涡旋脱落，并且各涡结构差异较大；以杆件结构为主的受电弓，在列车高速运行时引发周期性的涡脱落，产生以涡脱落频率为峰值主频的气动噪声；受电弓弓头处的声功率级最大，但对气动噪声的总贡献量并非最大，头车前转向架区域的气动噪声大于其他转向架。

（3）高速列车气动噪声存在明显尺度耦合效应，车头车尾及车身气动噪声受边界层影响较大，转向架区域受几何边界影响较大，受电弓区域与涡脱频率明显相关。

（4）不同区域的气动噪声流致发声机理并不相同，在捕捉到足够流场细节后，方可进一步研究其特性。

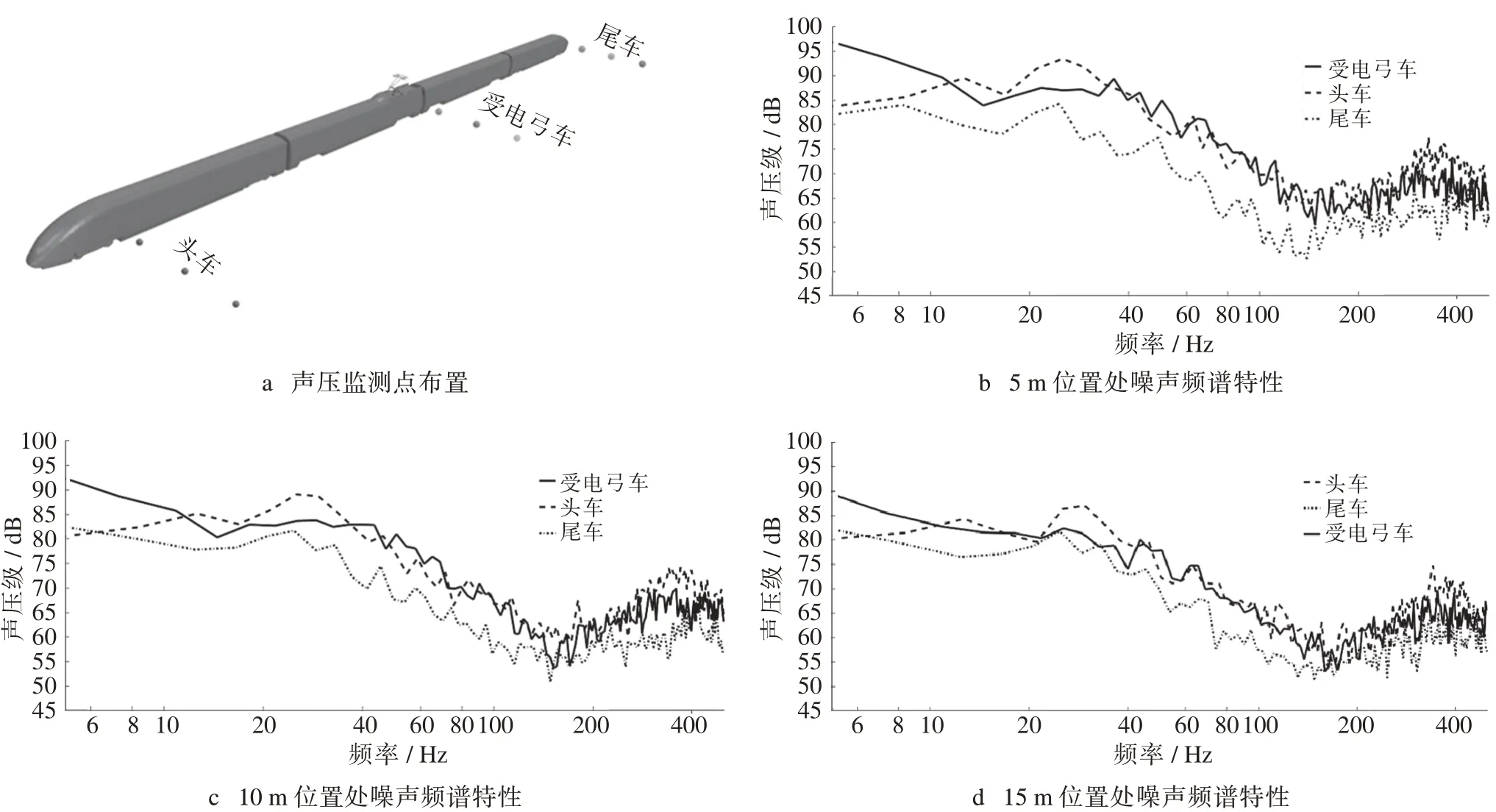
图6 列车近场声压频谱特性