考虑负荷方差的智能微网用户侧分时电价优化模型
杨国山 杨德州 杨昌海 徐慧慧 刘永成


摘 要:为调整用户用电行为,提升智能微网安全性和稳定性,需构建考虑负荷方差的智能微网用户侧分时电价优化模型。通过需求价格弹性系数描述用户对电价的反应情况,依照智能微网中负荷恒定状态和波动状态,计算线路可变损耗,取样采点一定周期内负荷,计算负荷方差,探析负荷方差对线路损耗的影响。依照负荷方差和用户负荷峰谷差构建智能微网用户侧分时电价优化的目标函数,设置峰平谷电价、用户利益、峰谷倒置等五个约束条件,结合约束条件和目标函数获取最终的优化模型。实验表明,该种方法构建的用户侧分时电价优化模型后,用户侧分时电价最大峰段负荷为14109 kW,峰谷差是7963 kW,显著增加售电侧和发电侧利润。
关键词:负荷方差;智能;微电网;用户侧;分时电价;优化模型
中图分类号:TM73 文件识别码:A
文章编号:1003—6199(2020)02—0098—06
Abstract:In order to adjust the power consumption behavior of users and improve the security and stability of intelligent microgrid,it is necessary to construct an optimization model of time-sharing electricity price on the user side of intelligent microgrid considering load variance. The response of users to electricity price is described by demand price elasticity coefficient. According to the constant and fluctuating state of load in intelligent microgrid,the variable loss of line is calculated,the load within a certain period of sampling point is calculated,the load variance is calculated,and the influence of load variance on line loss is analyzed. According to the load variance and the peak and valley difference of user load,the objective function is constructed,and the five constraint conditions,such as peak flat valley electricity price,user interest and peak and valley inversion,are set up,and the final optimization is obtained by combining the constraint conditions and the objective function. Model。 Through the experimental analysis,it is found that after the optimization model of the time-sharing electricity price on the user side,the maximum peak load of the time-sharing electricity price on the user side is 16324kW,and the difference between the peak and valley is 8143kW,which significantly increases the profit of the selling side and the generating side.
Key words:load variance;intelligence;microgrid;user side;time-sharing electricity price;optimization model
智能微網与传统电网相比,更为注重与用户之间的信息、电能和业务互动[1]。用户分布式能源利用和智能用电的有效载体是户用型智能微网,智能微网实现差异化供电和用户个性化的重要手段是户用型智能微网。随着网络通信技术、分布式发电技术和智能家居技术的不断发展,智能微网具有巨大潜力[2]。
目前随着世界能源短缺现象的出现,社会正在广泛关注电力的需求侧管理。电力需求侧管理的重要组成部分是用户侧分时电价,是当前学者研究的重点内容[3]。宋一航和于超等学者发现供电公司风险和用户侧分时电价之间的关系,曾鸣和刘敏等学者主要从销售侧和上网侧的角度出发,分析用户侧分时电价联动理论,张蓉和谭忠富从供电侧和发电侧角度的分级优化角度出发,探析用户侧分时电价理论,汤玉东和胡福年等学者从双边价格联动角度与用户侧分时电价之间关系,但是上述学者均未研究智能微网中负荷方差对用户侧分时电价的影响,忽略输电线路可变损耗和负荷方差间的关联性,且用户侧分时电价制定合理性较差。
因此从智能微网负荷方差角度出发,考虑了智能微网输电线路可变损耗和负荷方差间的关联性,构建智能微网用户侧分时电价优化模型。经过理论分析发现负荷高峰时期智能微网分时电价较高,负荷低谷时期智能微网分时电价价格较低,通过上述方法能有效引导智能电网用户转移负荷,降低智能微网中电力系统负荷波动情况,提升智能微网电力系统负荷率[4]。
1 分时电价优化模型
1.1 用户需求价格弹性系数
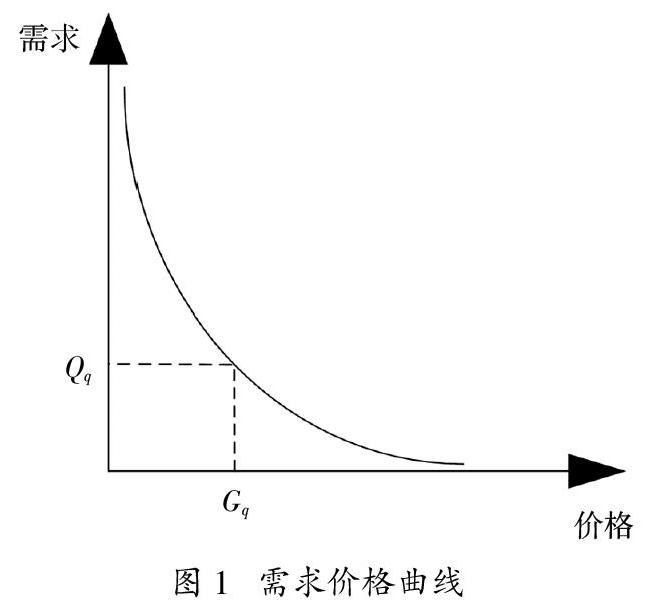
用户负荷影响因素较多,通常来说用户负荷影响因素包括电价、国民经济、生产方式等,其中电价是最为重要且操作性最强的一种影响因素[5]。电能中包含一般商品的共同属性,电能的价格和需求量之间存在负相关关系,两者之间关系如图1所示。
图1中可通过需求价格弹性系数描述用户对电价的反应情况,弹性系数描述公式如下所示:
式中,下标q和h分别表示调整用户侧分时电价前和调整用户侧分时电价后数据,o表示用户,ΔQ表示需求变化量,ΔG表示价格变化量,t1和t2表示不同时刻,当t1 = t2时,δ表示自弹性系数,否则δ表示交叉弹性系数[6]。当需求价格弹性系数已知时,可求调整用户侧分时电价后的用户用电量变化值,计算公式如下所示:
1.2 负荷方差特性对输电线路可变损耗影响
智能微网电力系统中电力损耗主要由两部分组成,一部分是可变损耗,一部分是不变损耗[7],其中智能微网变压器空载损耗和线路电晕损耗是不变损耗,不变损耗和线路上负荷之间没有关系[8]。智能微网中可变损耗是智能微网电路中线路负荷传输过程中导致的电能损耗,可变损耗的表达式如下所示:
式中■σ2表示负荷波动对智能微网输电线路可变损耗的影响,当用户总负荷数值处于既定状态时,σ2越小,负荷波动对智能微网中线路可变损耗影响越小[11]。由于从实际智能微网中获取完整的负荷曲线较为困难,需取样采点一定周期内的负荷,此时可计算负荷方差[12],计算公式如下所示:
1.3 分时电价优化模型
根据上述分析发现智能微网输电线路可变损耗和负荷方差之间存在一定联系,因此设计分时电价目标函数时需考虑负荷方差[13]。由于负荷方差无法充分反映负荷局部大幅度变化情况,需将负荷方差和用户负荷峰谷差有机结合,获取智能微网用户侧分时电价优化模型的目标函数[14],其中用户负荷峰谷差最小和用户负荷方差最小分别用下述公式表示:
确定上述目标函数后,需建立目标约束,总共有五个目标约束条件,如下所示:
(1)用户利益约束:智能微网实行分时电价后,用户的生活习惯和用电情况会受到一定影响,为获取更多用户的支持,需降低用户平均用电价格,此时用户利益约束为:
其中,Q表示不同时段用户需求量,P表示不同时段用户负荷有功功率。
(2)供电公司利益约束:为保障供电公司分时电价后的利益,需考虑供电公司运行成本和总售电收入,此时可获取供电公司利益约束:
式中,B表示供电公司允许减少收入的最大比例。
(3)峰平谷电价约束:当峰平谷中电价之间相差较小时,不同时间段的电价对用户激励作用较小,相差较大时,会对用户生活习惯和生茶习惯产生严重影响,对供电公司经济利益产生一定影响,阻碍实时分时电价。因此应将实施分时电价前后的电价比值控制在既定范围内[15],即峰平谷约束条件如下所示:
式中y1max、y1min分别表示峰电价和原电价比值上、下限,y2max、y2min分别表示平电价和原电价比值上、下限,y3max、y3min分别表示谷电价和原电价比值上、下限,y4max、y4min分别表示峰谷电价比值上、下限。
(4)用户总负荷约束:由于用戶平均用电发生变化,导致用户总负荷产生变化,为保障职能微网的稳定性,需约束用户总负荷,约束方程如下所示:
式中β表示实施用户侧分时电价后用户总负荷变化最大比值。
(5)峰谷倒置约束:为降低智能微网中出现峰谷倒置现象的几率,需设置条件约束峰谷倒置,约束条件如下所示:
经过上述分析可知,分时电价优化模型主要由目标函数和约束条件两部分构成,在考虑负荷方差的基础上,共同实现智能微网用户侧分时电价的有效优化。
2 实验分析
为验证设计优化模型的性能,需将设计模型应用到实际中。以某地区智能微网为例,假设依照用户价格弹性相似性可将该地区智能微网用户分成Ⅰ、Ⅱ两类,统计各个时段不同用户的负荷值如表1所示。
从表1中可以看出,与原负荷相比,Ⅰ类和Ⅱ类负荷变化范围发生变化,是原负荷的[0.91,1.24]和[0.71,1.49],依照上表可获取Ⅰ类和Ⅱ类负荷各个时间段的平均需求价格弹性系数,各个时间段需求价格弹性系数如表2所示。
从表2中可以看出,Ⅰ类负荷属于民用负荷,该负荷主要特点是休息时间弹性系数较高,工作时间弹性系数较低,Ⅱ类负荷属于工业负荷,各个时间段的弹性系数差距较小。应详细分析所选智能微网的用户侧分时电价。
2.1 不同负荷比例下分时电价分析
按照月用电量划分所选智能微网的用户侧分时电价,将用户侧分时电价划分成三个档次,假设第一梯度为0 kWh-180 kWh,第二梯度为181 kWh-270 kWh,第三梯度超过271 kWh,假设总负荷比例中第一梯度占有61%的比重,第二梯度占有31%的比重,第三梯度占有8%的比重,经过分析后本文方法构建优化模型后得到的负荷曲线变化和原始负荷曲线对比结果如图2(a)所示。如果第一梯度和第二梯度占有51%和36%的比重,第三梯度占有14%的比重,经过分析后本文方法构建优化模型后得到的负荷曲线变化和原始负荷曲线对比结果如图2(b)所示。
从图2(a)中可以看出,未采用本方法構建用户侧分时电价优化模型后,用户侧分时电价最大峰段负荷为16324 kW,峰谷差值为8143 kW,采用本方法优化模型后分时电价最大峰负荷是14109 kW,峰谷差是7963 kW,相差180 kW,用户总支出也发生变化,正在不断增加,与为实施分时电价相比略微增加,整体上智能微网用户舒适度可以得到提升,售电侧和发电侧利润都在不断增加。从图(b)中可以看出,经过本方法优化后最大负荷是14976 kW,峰谷差为6478 kW,与采用优化模型前相比最大负荷降低1012 kW,峰谷差降低1612 kW,用户支出降低,售电侧利润和发电侧利润逐渐增加。经过上述分析可以发现,当第二梯度和第三梯度负荷比例逐渐增加时,能够增加售电侧和发电侧的利润,但为保障居民用电状况,应保障第一梯度比例在一定范围内。
2.2 不同时段个数下净负荷期望值分析
为研究本方法构建智能微网用户侧分时电价优化模型的优化效果,需研究优化模型在不同时段个数下的净负荷期望值,结果如图3所示。
从图3中可以看出,采用本方法优化模型后,当划分时段个数为5时,用户侧分时电价调整效果较好,经过实际分析发现,当分段个数不断增加时,峰谷平划分更为明确,调节效果更好。因此在采用本方法构建用户侧分时电价优化模型时,应合理划分时段,提升分时电价优化效果。
3 结 论
经过调查分析发现,当前大部分智能微网用户侧分时电价优化模型主要是依照峰谷差分析分时电价效果。从负荷方差和线路损耗之间的关系出发,发现智能微网负荷曲线整体波动性可通过负荷方差表示。因此将智能微网用户侧分时电价优化的目标函数设置为峰谷差和负荷方差,选取适宜的约束条件,实现智能微网用户侧分时电价的有效优化。经过实验分析发现,构建智能微网用户侧分时电价优化模型优化效果较好,能显著降低智能微网负荷波动。
参考文献
[1] 唐巍,高峰. 考虑用户满意度的户用型微电网日前优化调度[J]. 高电压技术,2017,43(1):140-148.
[2] 王树东,杜巍,林莉,等. 基于合作博弈的需求侧响应下光储微电网优化配置[J]. 电力系统保护与控制,2018,46(1):129-137.
[3] 姜磊,专祥涛. 分时电价下直流微网优化运行和容量配置研究[J]. 电力科学与技术学报,2019,34(1):80-87.
[4] 王凌云,马奇伟,徐嘉阳. 基于MAS微电网的需求响应互动定价优化模型[J]. 可再生能源,2017,35(6):905-911.
[5] 邵靖珂,汪沨,谭阳红,等. 计及需求侧响应的微网经济优化调度[J]. 电力系统及其自动化学报,2016,28(10):31-36.
[6] 禹威威,刘世林,陈其工,等. 考虑电动汽车充电和需求侧响应的光伏微电网多目标优化调度[J]. 电力系统及其自动化学报,2018,30(1):88-97.
[7] 佟晶晶,温俊强,王丹,等. 基于分时电价的电动汽车多目标优化充电策略[J]. 电力系统保护与控制,2016,44(1):17-23.
[8] 罗大厅,吕林,刘迪. 考虑多负荷种类需求响应的DG容量与电动汽车协同规划[J]. 电测与仪表,2018,55(17):55-62.
[9] 陈泽兴,张勇军,许志恒,等. 计及需求价格弹性的区域能源中心建模与日前优化调度[J]. 电力系统自动化,2018,634(12):33-41.
[10] 王召健,陈来军,刘锋,等. 考虑可控负荷调节能力的多微电网分布式频率控制[J]. 电力系统自动化,2016,40(15):47-52.
[11] 白佩琳,雷霞,何建平. 多微电网系统的竞价机制设计[J]. 现代电力,2017,34(6):22-27.
[12] 闫涛,唐巍,王越,等. 基于储能多状态模型的含微网配电系统可靠性评估[J]. 电网技术,2017,41(7):2222-2228.
[13] 赵敏,沈沉,李顺昕,等. 采用联盟型博弈考虑停电风险的多微电网合作条件研究[J]. 控制理论与应用,2018,35(5):688-698.
[14] 刘胜,李晓明,夏俊峰. 考虑负荷容量的改进型二阶灵敏度分析SV系数在城乡配电网无功选址中应用[J]. 电测与仪表,2018,55(18):32-36.
[15] 孙丛丛,王致杰,江秀臣,等. 计及需求响应的并网型微电网协同优化策略[J]. 电力系统及其自动化学报,2018,30(1):30-37.

