基于HHT的风力发电系统电压暂降检测研究

边辉 孙屹岱

摘   要：风力发电系统输出具有随机性、波动性和间歇性等特点，风力发电系统电压波动较为频繁，电压暂降已成为风力发电系统中最常见的电压波动。针对风力发电系统电压暂降问题，提出了一种基于Hilbert-Huang变换（HHT）检测方法，能够准确、及时地检测到电压暂降。为了解决HHT中经验模态分解（EMD）过程中的端部效应问题，采用了一种自适应的改进波形匹配方法对电压暂降问题进行处理。借助HHT中各固有模态函数（IMF）的电压幅值和频率两个参数反映电压波动，并通过Matlab仿真验证了该方法的实用性。

关键词：Hilbert-Huang变换;风电系统;电压暂降;电压检测

中图分类号：TP399                                            文献标识码：A

文章编号：1003—6199（2020）02—0046—04

Abstract：In view of the random，fluctuating and intermittent characteristics of the wind power system output，the voltage fluctuation of the wind power system is relatively frequent，and the voltage sag has become the most common voltage fluctuation in the wind power system. Aiming at the problem of voltage sag in wind power generation system，a detection method based on Hilbert-Huang transform （HHT） is proposed，which can accurately and timely detect the voltage sag. In order to solve the end effect problem in the process of empirical mode decomposition（EMD） in HHT，an adaptive and improved waveform matching method is proposed to deal with the voltage sag problem. The voltage amplitude and frequency of each inherent modal function（IMF） in HHT are used to reflect the voltage fluctuation，and the practicality of the method is verified by Matlab simulation.

Key words：Hilbert-Huang transformation;wind power system;voltage sag;voltage detection

充分利用風电能源，不仅能创造可观的经济效益，而且能有效缓解传统能源短缺带来的压力，还可以提供长期有效的能源供应[1]。目前，风电系统电压暂降检测常用的方法主要有平方检测法[2]、半波均方根检测法[3]和小波变换检测法[4]等。这些方法也存在一定的不足。平方检测法忽略了电压暂降时的频移分量[5]，半波均方根检测法需要采集半周采样数据才能得到结论，不能保证实时性，且该方法只能用于实时性要求不高的工况条件[6]。小波变换检测法适用于含有一个、两个或两个以上频率的波信号。但它要求同步信号和载波信号具有相同的相位、相同的频率和严格的分频。

为了有效地实时检测风电系统电压暂降的发生时间和幅度，以便实现实时的补偿措施，提高风电系统的供电可靠性和电能质量。利用改进Hilbert-Huang变换（HHT）方法来检测风力发电系统中的电压暂降问题。该方法采用波形匹配法对电压暂降问题进行处理，从而解决经验模态分解（EMD）过程中的端部效应，并通过仿真结果验证了该方法的实用性。

1   Hilbert-Huang变换（HHT）

Hilbert-Huang变换是一种新的信号分析方法。该方法由经验模态分解（EMD）和希尔伯特变换组成[7]。通过EMD分解将信号分解为一系列固有模态函数（IMF），从而得到局部限制而非全局限制。固有模态函数是一个近似于单个频率分量的信号，这意味着在任何时候都只有一个信号频率分量[8]。对于HHT的每个固有模函数，可以得到每个IMF的瞬时谱。

1.1   经验模态分解（EMD）过程

根据信号x（t）的最大值和最小值，求出上包络线x1（t）和下包络线x2（t）的平均值：

然后计算x（t）和μ1 之差为：

如果θ1满足IMF的两个条件：（1）超过极值点和零点的点的数量相同且最多不超过一个;（2）信号与时间轴对称。θ1是x（t）的第一个IMF分量。如果θ1不满足IMF的两个条件，则将θ1作为原始数据。重复上述过程k次，得到θ1k = θ 1（k-1） - μ1k，然后用SD判断每个筛选结果是否为IMF分量：

其中，SD可根据实际要求确定。如果θ1k满足 SD的要求，则令α1 = θ1k，α1是信号x（t）的第一个IMF分量，将α1与x（t）分离为：

取r1为新的x（t），重复上述过程，可以得到α2，α3，α4，…，直到rn是单调的或者|rn|很小，分解的结果如下：

1.2   Hilbert变换

1.3   端部效应

在经验模态分解（EMD）过程中，需要根据IMF计算过程中的包络线来计算信号的局部平均值[9]。通过对信号的局部最大值和局部最小值进行三次样条插值算法[10]分别得到上、下包络线。由于信号的两个端点不一定能够满足插值要求的出界点，所以可能会带来一定的误差，这种情况称为端部效应[11]。为了解决经验模态分解（EMD）过程中的端部效应问题，提出了一种自适应的改进波形匹配方法对对电压暂降问题进行处理。

2   自适应改进波形匹配方法

在端部效应抑制方面，常用的方法有镜像延拓法、基于神经网络的延拓法[12]、基于多项式拟合的延拓法[13]等，这些方法在一定程度上抑制了端部效应。但它们也有一些问题。为了快速检测风电系统电压暂降，采用改进波形匹配自适应方法对电压跌落问题进行处理。波形匹配方法的核心是：根据自然信号的规律，假定信号的发展和变化总是遵循一定的规律。信号在边界处的发展趋势也将反映在内部信号中，特别是对于正则性强的信号将更加明显。为了检验连续波形的真实程度，需要引入波形匹配度[14]的概念来检验连续波形的真实性。

假设f1（t）和f2（t）是两个长度都为N的数据序列。S1（t，f1（t））和S2（t，f2（t））是f1（t）和f2（t）上的两个点。根据以下步骤可以得到f1（t）和f2（t）相对于S1和S2的波形匹配度。

（1）变换f1（t）与S1和S2重合，新波形为f  *1（t）;

（2）根据公式获得相对于S1和S2的f1（t）和f2（t）的波形匹配度：

波形匹配方法的具体步骤如下：

步骤1：获取原信号f（t）的所有极值点Mi，将最大点置于{Mi，max}，最小点置于{Mi，min};

步骤2：第一个最小点为M0，第一个最大点为Mi。M1和f（t）在开始时间之间的距离是sd0。sd0的长度是l;

步骤3：所有Mi，max相对于sd0的波形匹配度均为mdi;

步骤4：mdi的最小波段为sdi，当mdi <α·l（α是由匹配精度要求确定的常数）时，则取mdi作为f（t）左端的波形延拓。否则，按步骤（5）进行处理;

步骤5：直接指定端点的极大值和极小值。将原始信号最左侧推导的两个相邻最大点的平均值为左侧的最大值，将原始信号最左侧推导的两个相邻最小点的平均值为左侧的最小值。

3   仿真分析

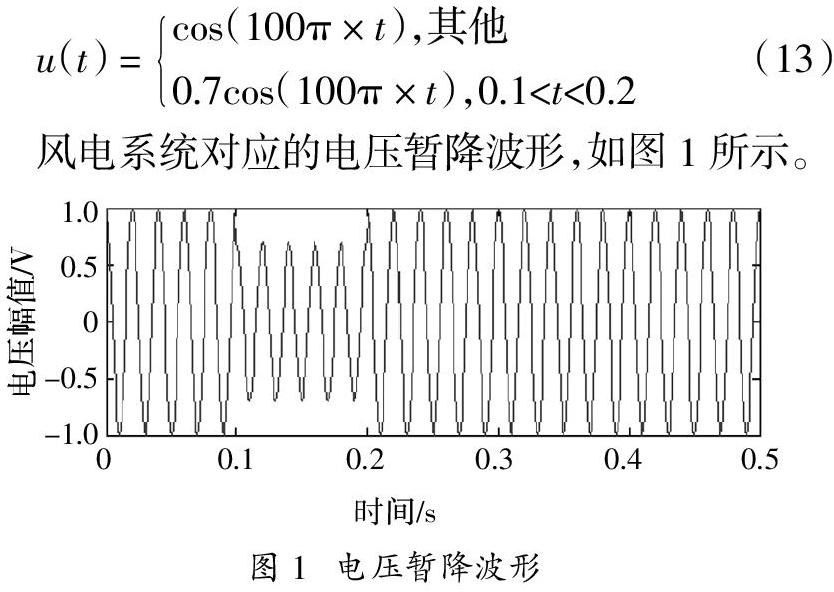
现实工况条件下，由于自然环境对风电系统电压的影响，使得风电系统的波动更加复杂。对风电系统电压波动的电压暂降进行仿真分析。在非下垂期间，假设风电系统电压波形始终保持不变（幅值为额定电压，频率为50 Hz）。电压暂降通常是指均方根电压迅速降到额定电压的90%至10%，然后迅速恢复到正常电压。其典型持续时间为0.5-30个周期[15]。因此，假设风电系统电压RMS暂时降低到额定电压的70%，并且持续时间为5个周期。则电压函数为：

风电系统对应的电压暂降波形，如图1所示。

针对电压暂降问题，首先将Matlab中的波形匹配数据延拓子程序应用于原始信号的扩展中，有效地避免了HHT变换过程中的端部效应。然后调用Hilbert-Huang变换程序对连续信号进行HHT处理，并输出IMF1的幅值和时间、频率和时间的关系曲线。最后，根据IMF1的幅值和时间、频率和时间的关系曲线，得到了风电系统发生电压暂降时的电压幅值和电压频率，有助于判断电压暂降的时间和幅值，HHT仿真结果如图2和图3所示，并对仿真结果进行了基于端点处理的波形匹配自适应。

在仿真中，假设在0.1-0.2 s后出现电压暂降，从HHT仿真结果可以看出，在0.1 s或0.2 s时，电压仅为额定电压的0.62倍;在0.1 s或0.2 s附近，瞬时频率也有很大的变化。最高频率高达78.64 Hz，最低频率仅为19.8 Hz。根据电压参数的变化，可以实时、有效地判断风电系统的电压暂降情况。

如果风电系统电压RMS暂时降至额定电压的80%，持续时间为0.5个周期，则电压函数为：

对应的电压波形，如图4所示。

风电系统的电压暂降参数为：均方根电压暂降到额定电压的80%，持续时间为0.5个周期。基于改进HHT的波形匹配自适应端点处理后的HHT仿真结果分别如图5和图6所示。

HHT仿真结果表明，在0.2 s的半周期启动过程中，风电系统电压发生变化。在0.2 s时，风电系统的最小电压为额定电压的0.77倍。在0.2 s时，瞬时频率也有很大的变化，最高频率為68.4 Hz，最低频率仅为32.2 Hz。因此，根据电压参数的变化，可以实时、有效地判断风电系统的电压暂降情况。

4   结   论

将Hilbert-Huang变换方法（HHT）应用于风电系统电压暂降的实时精确检测。为了解决EMD分解时的端点效应，采用波形匹配自适应数据延拓技术对端点波形进行管理。Matlab实例仿真结果表明，HHT能够有效实时地检测风电系统的电压暂降情况，能够准确判断电压暂降时刻和暂降后的电压幅度以及电压暂降持续时间。风电系统输出电压受自然环境影响，输出电压波动较大。实际问题比本研究的电压暂降问题更为复杂，电压波动的检测也更为困难。所采用的检测方法特别适用于风电系统电压暂降的检测。为了加强风电系统的控制，还需要对其他电压波动问题进行进一步的研究。

参考文献

[1]    李海波. MW级双馈风力发电系统控制策略研究[J]. 电器与能效管理技术，2018（24）：60-65.

[2]    秦建，王帅，李剑，等. 基于滑动数据窗的电压暂降检测方法与装置[J]. 自动化与仪表，2018，33（11）：67-70.

[3]    胡雷，陈湘波，熊魁，等. 基于改进HHT的电能质量扰动检测方法[J]. 电测与仪表，2018，55（21）：105-111.

[4]    管高翔. 利用小波变换定位与辨识短时电压变动[J]. 电脑与信息技术，2018，26（03）：29-32.

[5]    张军，陈兵，张国江，等. 不同电压暂降临界持续时间的检测[J]. 机械与电子，2018，36（10）：38-43.

[6]    李堃，刘晓波，张明浩，等. 基于蒙特卡洛和虚拟节点法的电压暂降正反分析[J]. 电力科学与工程，2018，34（08）：43-49.

[7]    王震，李志华，邵新添. 基于改进的EMD方法的模拟电路故障诊断研究[J]. 信息技术，2017（12）：37-40.

[8]    周柏彤，刘增力，朱健晨. 关于多种模态分解方法的分离效果的差别探讨[J]. 信息技术，2016（12）：87-92.

[9]    邢昀，荣剑. 常见不同模态信号分解方法探讨[J]. 现代计算机（专业版），2018（36）：7-11.

[10]  刘毅，宋余庆，刘哲. 基于有理四次Hermite插值和PSO的EMD包络线拟合算法[J]. 电子学报，2018，46（11）：2761-2767.

[11]  徐健，張禹，吴飞飞. 基于改进HHT算法的谐波信号分析方法[J]. 电子测量技术，2018，41（08）：30-34.

[12]  李绪琴，陈文静，苏显渝. 基于改进经验模态分解的三维重建[J]. 四川大学学报（自然科学版），2018，55（01）：111-117.

[13]  杨波，李世平. 一种基于GEP的EMD端点效应抑制方法[J]. 中国测试，2015，41（12）：32-35.

[14]  王录雁，王强，鲁冬林，等. EMD自适应三角波匹配延拓算法[J]. 振动与冲击，2014，33（04）：94-99.

[15]  徐健，郭涛. 基于改进HHT与改进S变换相结合的电能质量扰动检测仿真分析[J]. 自动化技术与应用，2018，37（05）：98-102.