切比雪夫滤波器在控制系统中的应用

李凡营　蔡杰

摘 要：针对振动电磁等强干扰条件下编码器读数易受噪声影响的问题，本文从工程实际出发，提出了一种带滤波的复合控制系统。首先，详细分析了切比雪夫滤波器的特点，然后介绍了带低通滤波器的复合控制系统原理，最后通过仿真证明了本方法的正确性和有效性。

关键词：编码器;复合控制;切比雪夫滤波器

中图分类号：TH133.7文献标识码：A文章编号：1003-5168（2020）13-0048-03

Application of the Chebyshev Filter in Complex Control System

LI Fanying CAI Jie

（The 713th Institute of China Ship Industry Corporation CSIC，Zhengzhou Henan 450015）

Abstract： In view of the problem that the encoder reading was easily affected by noise under the condition of strong electromagnetic interference， this paper proposed a compound control system with filter based on the engineering practice. Firstly， the characteristics of Chebyshev filter were analyzed in detail， and then the principle of composite control system with low-pass filter was introduced. Finally， the correctness and effectiveness of this method were proved by simulation.

Keywords： encoder;complex control;Chebyshev filter

編码器是把角位移或直线位移转换成电信号的一种装置。按照工作原理编码器可分为增量式和绝对式两类。增量式编码器转动时输出脉冲，通过计数设备来知道其位置。绝对式编码器旋转一周过程中每个机械位置对应于一个唯一绝对的编码，所以其无须记忆，而且无须一直计数，控制器什么时候需要知道位置，什么时候就去读取它的位置。失电后无须控制器记忆当前位置，待下次上电时直接读取位置即可。绝对式编码器的便利性与自身带有的记忆性特征使其广泛应用于各种位置测量场合[1]。但是，在某些特定的情况下，编码器读数头读数易受到震动、电磁污染等环境干扰，从而使控制系统控制精度急剧下降。本文从消除环境干扰提高编码器数据信噪比出发，提出在编码器输出数据后增加一高性能切比雪夫低通滤波器来提高系统的抗干扰性，并通过仿真验证了该方法的正确性。

1 切比雪夫低通滤波器

切比雪夫滤波器的幅度特性是在一个频带内（通带或阻带）具有等波纹特性。一种是在通带内是等波纹的，在阻带是单调的，称为切比雪夫Ⅰ型;一种是在通带内是单调的，在阻带内是等波纹的，称为切比雪夫Ⅱ型。为了使高频干扰的影响降到最低的同时获得通带内信号的等波纹特性，研究者选用切比雪夫Ⅰ型低通滤波器。

切比雪夫Ⅰ型低通滤波器的幅度平方函数为：

其中，[ε]为小于1的正数，表示通带波纹大小，[ε]越大，通带波纹也越大;[Ωc]为截止频率;[ΩΩc]为[Ω]对[Ωc]的归一化频率，也是滤波器的某一衰减分贝处的通带宽度;[TN]为切比雪夫多项式，定义如下：

将其展开成多项式的形式，可以得到以下的递推公式：

定义通带最大衰减（分贝）为：

其中在通带内：

将（7）和（8）带入（6）可得：

阻带截止频率为[Ωst]，则当[Ω≥Ωst]时，有

其中，[A]为一常数。由于切比雪夫Ⅰ型滤波器在阻带内为单调下降，所以若用阻带最小衰减[δ2]表示，则有

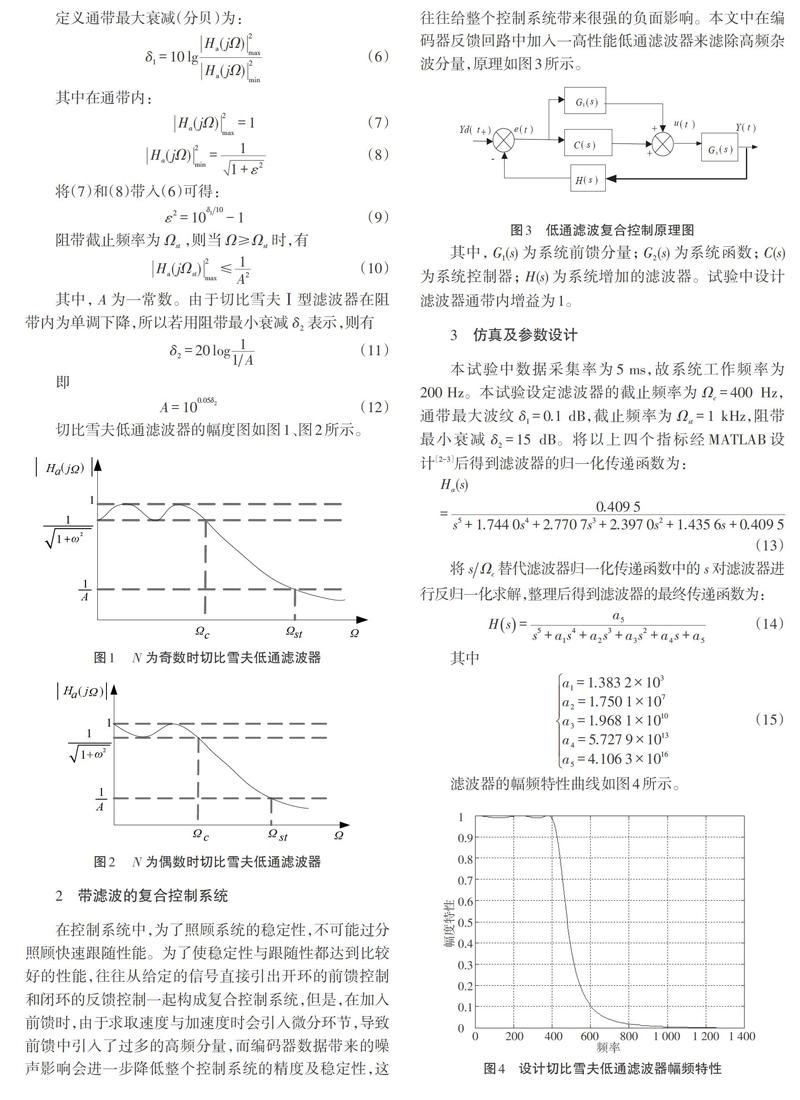
切比雪夫低通滤波器的幅度图如图1、图2所示。

2 带滤波的复合控制系统

在控制系统中，为了照顾系统的稳定性，不可能过分照顾快速跟随性能。为了使稳定性与跟随性都达到比较好的性能，往往从给定的信号直接引出开环的前馈控制和闭环的反馈控制一起构成复合控制系统，但是，在加入前馈时，由于求取速度与加速度时会引入微分环节，导致前馈中引入了过多的高频分量，而编码器数据带来的噪声影响会进一步降低整个控制系统的精度及稳定性，这往往给整个控制系统带来很强的负面影响。本文中在编码器反馈回路中加入一高性能低通滤波器来滤除高频杂波分量，原理如图3所示。

其中，[G1（s）]为系统前馈分量;[G2（s）]为系统函数;[C（s）]为系统控制器;[H（s）]为系统增加的滤波器。试验中设计滤波器通带内增益为1。

3 仿真及参数设计

本试验中数据采集率为5 ms，故系统工作频率为200 Hz。本试验设定滤波器的截止频率为[Ωc=400] Hz，通带最大波纹[δ1=0.1] dB，截止频率为[Ωst=1] kHz，阻带最小衰减[δ2=15] dB。将以上四个指标经MATLAB设计[2-3]后得到滤波器的归一化传递函数为：

将[sΩc]替代滤波器归一化传递函数中的[s]对滤波器进行反归一化求解，整理后得到滤波器的最终传递函数为：

其中

滤波器的幅频特性曲线如图4所示。

本试验中选用控制系统的传输函数为：

对[G2（s）]求取其倒数中的速度分量，省略加速度及其高阶分量，得到前馈速度为：

控制器选经典PID控制[4]，其中[P]=0.45，[I]=9，控制器的传输函数为：

4 仿真结果及分析

本试验中输入信号为幅值为1，频率为0.32 Hz的正弦波信号，外加均方根为0.05的高斯白噪声。其仿真结果如图5至图7所示。

从图5、图6及图7可以看出，在相同PID参数时，传统PID控制下系统跟随正弦信号的快速性和前馈控制相比要差很多，且加入滤波器后较传统复合控制相比，带切比雪夫滤波的PID复合控制系统收敛速度几乎不变。但是，传统PID控制系统稳定段的误差最大幅值为0.319，复合控制下系统跟随输入信号的最大误差为0.002 7。在速度前馈信号上增加一切比雪夫滤波器后，系统跟随输入信号稳定后的最大误差幅值为0.000 32，与传统直接前馈相比，复合控制精度几乎提高了一个数量级。这充分证明了该方式的有效性与正确性。

参考文献：

[1]马净，王峰，李晓光，等.编码器原理及应用[J].中国仪器仪表，2002（5）：43-45.

[2]贾宝富，王一凡，罗正祥.广义切比雪夫线性相位滤波器设计[J].电子科技大学学报，2008（3）：389-392.

[3]赵金.微弱信号在数字信号处理器上的检测与实现[J].电子测试，2008（3）：75-78，82.

[4]刘金琨.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社，2011.

收稿日期：2020-04-12

作者简介：李凡营（1988—），男，硕士，研究方向：火控解算与伺服系统。