基于冲击弹性波的隧道衬砌混凝土强度检测技术研究和应用

姜勇 吴佳晔 马永强 黄伯太

（1.中国国家铁路集团有限公司工程质量监督管理局，北京 100844；2.四川升拓检测技术股份有限公司，成都 610046；3.西南石油大学，成都 610500）

铁路隧道衬砌由于施工等多方面原因，其混凝土质量问题多发，作为质量评价基本指标的强度检测显得尤其重要。根据TB 10417—2018《铁路隧道工程施工质量验收标准》规定，铁路隧道混凝土强度检测主要方法为回弹法和取芯法。回弹法检测深度浅，误差大；取芯法代表性差，对结构有一定损伤［1］。检测结果往往不能全面、有效地反映混凝土结构的实际强度，为施工质量把控、监督检查等带来很大困惑。

本文分析了混凝土强度常用检测方法，并就冲击弹性波检测混凝土强度的基本原理，以及其在铁路隧道衬砌质量检测中的验证、应用等进行论述。

1 常用检测方法

混凝土强度检测方法大致可以分为两类：有损检测（钻芯取样+压载试验）和无损检测（回弹法、超声回弹法等）。

1.1 有损检测方法

一般认为钻芯取样+压载试验是最可靠的混凝土强度检测方法，但存在以下两方面问题。

1）代表性差。芯样通常为直径10 cm 圆柱状试样，在进行压载试验前需切削整形并加工成高度为10 cm 左右的圆柱体，体积约为0.8×10-4m3，相对隧道一板衬砌的方量（约120 m3），仅占比0.000 65‰，即使按一板3个芯样，其代表性也不到0.002‰。

2）对结构有一定损伤。钻孔后尽管会进行填充修补，但修补效果往往无法验证和确认。图1 为某铁路隧道衬砌多次取芯检测后的情形，2 m2左右范围内钻孔21处，势必会对结构的耐久性产生不利影响。

图1 取芯检测后隧道衬砌

1.2 无损检测方法

1.2.1 回弹法

回弹仪具有结构简单、操作方便等优点，长期以来是最主要的现场检测设备之一，但也存在以下三方面问题。

1）检测范围浅。回弹仪的检测深度仅限于混凝土表层，无法对内部结构进行检测。

2）检测精度低。回弹仪的检测受表面状况（凹凸、湿度等）影响很大，且需要碳化修正。

3）属于机械式。摩擦等造成的误差易积累。

铁路隧道衬砌厚度一般在35～60 cm，通常采用插入式振捣器和附着式振捣工艺，使得衬砌表面混凝土与内部混凝土间可能存在较大差异，因此回弹仪不能满足检测范围要求。图2为某铁路隧道衬砌回弹检测值与钻芯压载值对比，可知回弹仪与钻芯压载值之间几乎无相关性。

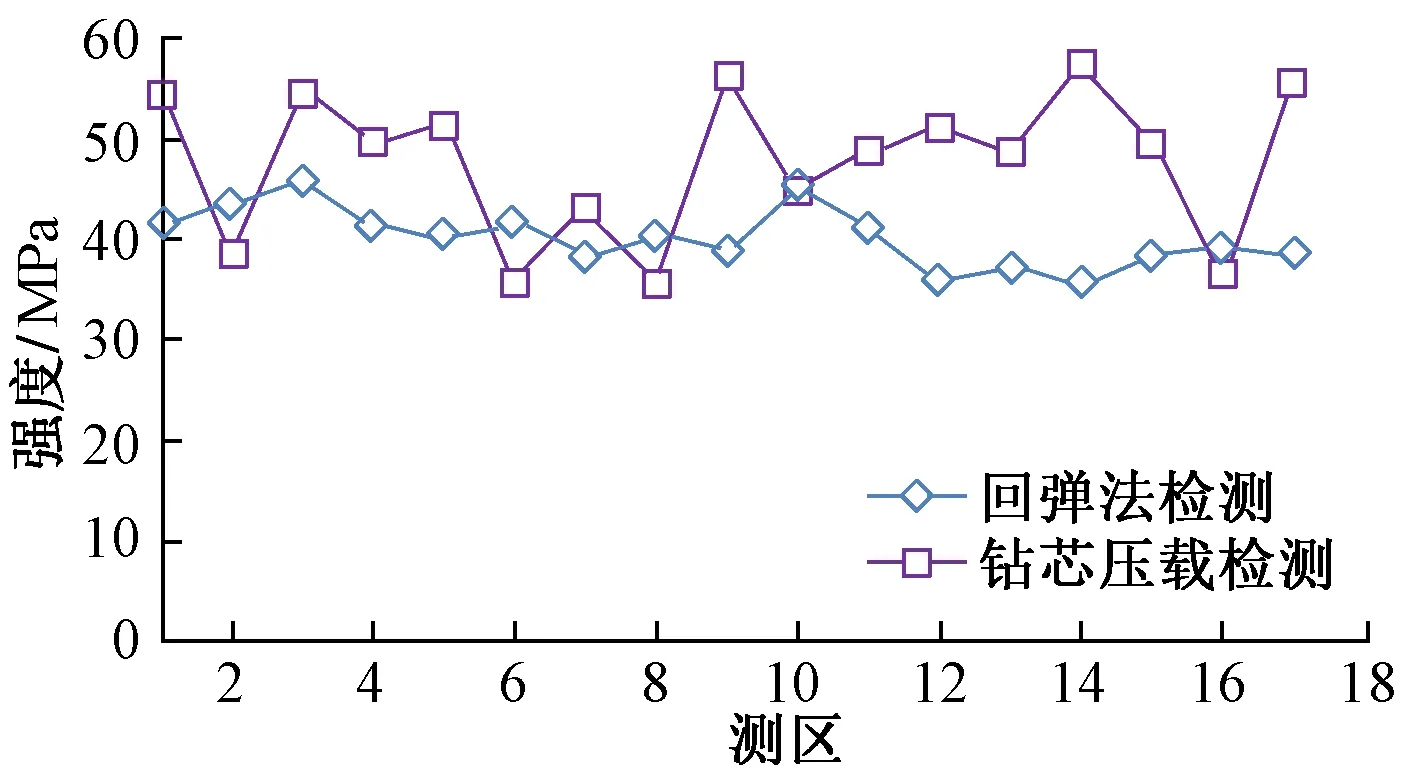
图2 混凝土强度检测对比

1.2.2 超声波法和超声回弹综合法

超声波法和超声回弹综合法虽然被列入多个检测规范，但由于检测精度差、效率低等原因在隧道衬砌检测中应用较少。其中，超声波频率对检测波速的影响、标定状态（对测）与实际检测（平测）状态的差异是主要误差原因，同时检测深度同样局限于衬砌表层，降低了检测代表性。

1.2.3 其他方法

DBJ04∕T 339—2017《冲击弹性波检测混凝土质量技术规程》中规定了基于冲击弹性波P 波的混凝土强度检测方法。此外，采用面波（又称瑞利波）法对检测仅有一个作业面且厚度未知的混凝土结构是有效的［2-4］。但是，采用冲击弹性波在检测结构混凝土的实际应用还十分少见，其原因主要有以下三方面。

1）未能很好地解决标定问题。为了建立测强曲线，需利用试件进行波速—强度关系标定。然而即使是同种材料，不同形式或尺寸试件，其检测得到的弹性波波速也有所不同。同时，实际结构尺寸和形状与试件差别更大，即使采用钻芯标定，由于芯样仅能代表检测结构区域局部，使得测强曲线可靠性也难以保障。

2）未考虑钢筋影响。混凝土结构中大多有钢筋，由于钢筋的波速快于混凝土的波速，因此钢筋含量会对检测的波速产生影响。

3）未解决不同检测方法波速换算问题。根据检测对象、作业面等不同，冲击弹性波检测可以分为平测法、对测法和反射法。其中，对测法和反射法均利用弹性波中P 波成分，而平测法则分为利用P 波和R 波（亦即面波、瑞利波）两种。此外，对测法P 波又分为一维、二维和三维，反射法根据解析方法也可分为单次反射和多次反射（亦称冲击回波法）等。检测方法众多，在提高适用性的同时，由于各检测方法得到的波速均不同，使得分析难度大幅增加。

图3为现行混凝土强度检测流程，可知不同方法、不同对象间标定的波速—强度曲线是相互割裂的，为实际应用带来很大困扰。

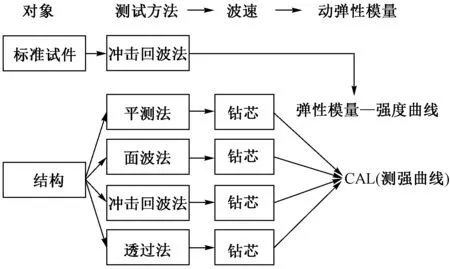
图3 现行混凝土强度检测流程

2 基于冲击弹性波的混凝土强度检测体系

基于冲击弹性波的混凝土强度无损检测技术体系，以动弹性模量Ed作为桥梁，连接标定和现场检测并统一了各种检测方法，见图4。

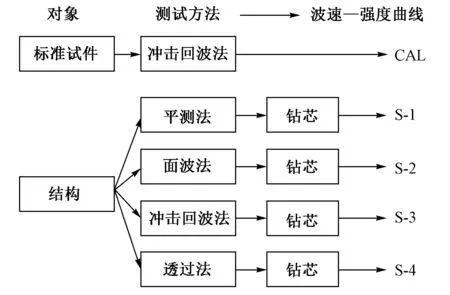
图4 基于冲击弹性波的混凝土强度检测流程

本体系的核心在于首先测出混凝土材料的动弹性模量Ed，再建立其与混凝土抗压强度fcu的关系。这样只要混凝土材料相同，无论是试件、构件，也无论哪种检测手段，均可以采用同样的fcu-Ed测强曲线，从而大大简化标定流程并可提高检测精度。

同时，通过对钢筋影响的修正，进一步提高混凝土强度的标定精度。

2.1 动弹性模量检测及验证

混凝土动弹性模量Ed可根据弹性波理论，通过冲击弹性波波速和材料密度计算。但不同的检测方法和结构形态，其计算方法也不同。

2.1.1 透过法和平测法

根据被测体的形状及采用的冲击弹性波成分，可分为一维P波、二维P波、三维P波和瑞利（面）波。

1）一维P 波VP1。对于可视为一维弹性体的杆件结构，动弹性模量Ed与弹性波一维P波波速VP1的关系可以表示为

式中：ρ为混凝土密度，一般约为2 400 kg∕m3。

2）二维P 波VP2。对于可视为二维弹性体的板式结构，则

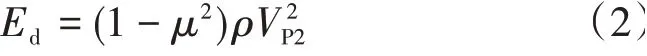
式中：μ为混凝土动泊松比，一般为0.25～0.30［5］。

3）三维P 波VP3。对于可视为三维弹性体的块体结构，则

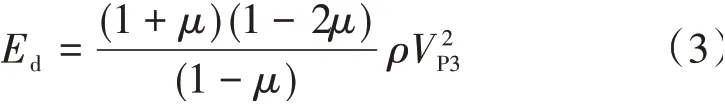
4）瑞利（面）波VR。对于厚板结构，若采用面波（瑞利波），则

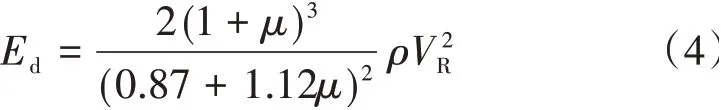
当混凝土动泊松比μ取0.25 时，弹性波不同成分速度间相对关系见表1。

表1 不同成分波速间的相对关系

2.1.2 反射法

无论是对于基桩这样的单次反射，还是对试件采用的多次反射（冲击回波法），根据检测波速均可换算成一维P波波速VP1。

式中：H为试件检测方向的高度或长度；T为激振弹性波往返时间或卓越周期；α为一维波速换算系数，根据试件尺寸（宽高比），取1.01～1.12。

根据吕小彬、吴佳晔等研究成果［5］，基于冲击弹性波检测动弹性模量的精度符合相关要求，且效果较好；对于棱形试件，冲击弹性波法与共振仪法的结果相对误差低于2%，冲击弹性波法检测稳定性等优于共振仪法。

2.2 fcu-Ed测强曲线

由于弹性模量与抗压强度均属于混凝土本身的力学特性指标，具有良好的相关关系。根据GB 50010—2010《混凝土结构设计规范》，混凝土弹性模量与抗压强度等级关系见表2。

表2 混凝土弹性模量与抗压强度等级关系 GPa

表2 中为弹性模量Ec而非动弹性模量Ed，无法直接用于冲击弹性波检测。为此，提出基于Sigmoid 曲线的fcu-Ed模型，即

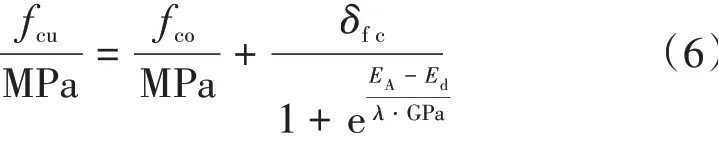
式中：fco为混凝土最小抗压强度，取5 MPa；δfc为最大混凝土强度与最小抗压强度的差值，取80 MPa；EA为Sigmoid曲线中点对应的动弹性模量，单位为GPa；λ为形状决定系数。

因此，模型参数可简化为EA和λ，则

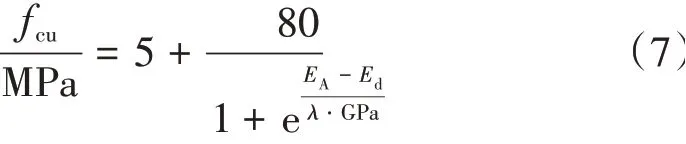
通过分析不同材料、配比、成分的324个试块和芯样弹性波及压载试验，fcu-Ed测强曲线见图5，应用最小二乘法回归得出EA=39.5 GPa，λ=5.5。

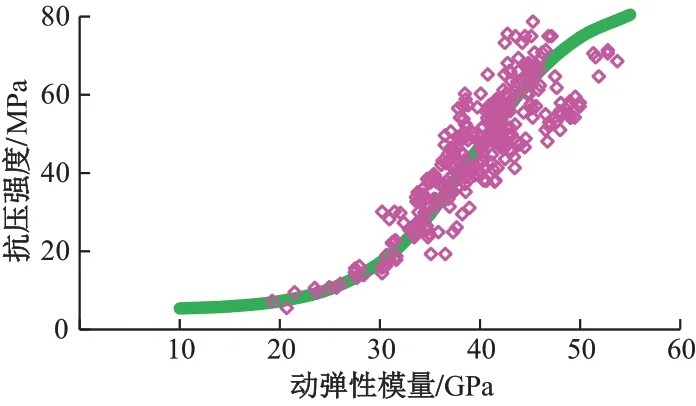
图5 fcu-Ed测强曲线

本文提出的fcu-Ed测强曲线模型最大特点是采用Sigmoid函数作为基底，与通常的指数或幂函数基底相比，强度推算时稳定性好，离散性较小。但本模型在高强度（超过70 MPa）时推算的混凝土强度有偏低倾向。因此，目前该模型仅适用于强度70 MPa 以下混凝土。

2.3 fcu-Ed测强曲线标定

由图5 可知，不同混凝土，抗压强度fcu、动弹性模量Ed分布有一定的离散性，因此标定对提高检测精度是有帮助的。

标定一般采用预留标准试块或钻芯得到的试样来进行。根据标定样的数量和强度分布范围，可以分为标准标定和简易标定两种。

2.3.1 标准标定

1.3疗效判定方法我们将患者的临床治疗分成了三个等级。显效:患者的瘤体完全被切除,使用CT检测,没有发现残留,病灶完全消失;有效:患者的瘤体缩小至少50%,存在部分残留。无效:患者的瘤体缩小不足25%,有超过一半的病灶残留。

当用于标定的试件（芯样）较多且强度分布范围较广，如最大最小强度差在20 MPa 以上时，可采用最小二乘法对EA和λ进行标定。

2.3.2 简易标定

当用于标定的试样较少或分布比较集中时，对动弹性模量EA和形状决定系数λ同时进行回归反而会引起较大的误差，此时可采用简易标定。

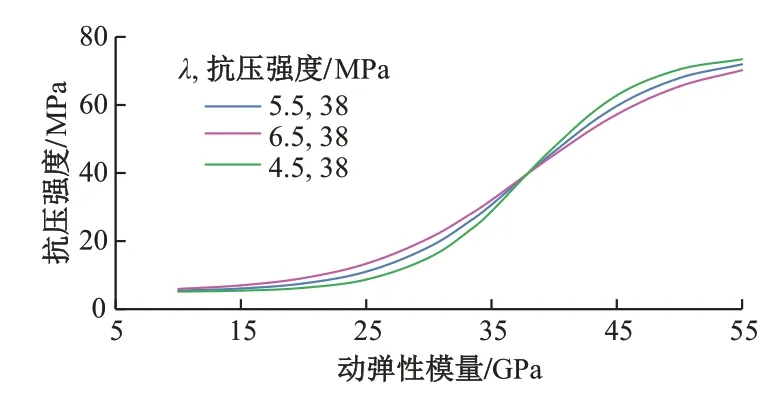
图6 不同形状决定系数λ对曲线形状的影响

首先确定λ。不同λ对曲线形状的影响见图6，λ越大，S 形中间段越陡，反之，则越平缓。对于大多数结构混凝土（抗压强度20～75 MPa），λ为4～7。在确定λ以后，即可简单地确定动弹性模量EA。

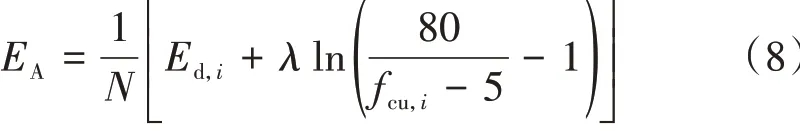
2.4 钢筋影响及修正

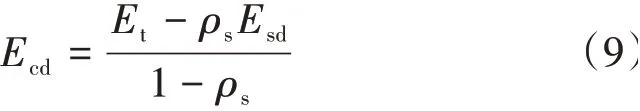
由于使用的冲击弹性波波长较长（约200 mm 以上），远大于钢筋直径，因此可将钢筋与混凝土考虑成复合材料，并根据综合配筋率ρs加以修正。式中：Ecd为修正后混凝土动弹性模量；Et为未经修正检测动弹性模量；ρs为综合钢筋率（近似于钢筋体积系数）；Esd为钢筋动弹性模量，取210 GPa。

3 铁路隧道衬砌混凝土强度验证及应用

混凝土强度检测技术体系及相关的检测设备已在十余条铁路线156 座隧道中得到验证和应用，见表3。

表3 在铁路隧道衬砌中的应用（设计强度35 MPa）

3.1 检测方法及参数

3.1.1 标定

标定采用预留标准立方体试块，以及钻芯取样后制作的试件（ϕ100 mm×100 mm），利用冲击弹性法检测。但许多预留试块的配比、振捣及养护均与实体结构混凝土有较大的差异，无法起到预想的标定作用。

3.1.2 现场检测

根据铁路隧道衬砌的特性，可用的冲击弹性波检测方法只有P 波平测法和瑞利波法两种。由于P 波平测法反应的深度范围较浅，而且检测时间较长，经过对比，选择瑞利波法。

图7（a）是典型的瑞利波检测波形，可见信噪比高，易于分析。同时，开发了全自动解析和自动生成报告程序，从检测到解析，一个测区的平均耗时3～5 min，与回弹仪检测耗时相近。

根据卓越波长法，可以得到瑞利波频散曲线（亦即不同频率下瑞利波的波速分布）［5］，见图7（b）。

根据瑞利波波速，利用式（4）和式（8）不仅可以得到混凝土强度，还可以得到其沿深度方向的分布，见图7（c）。

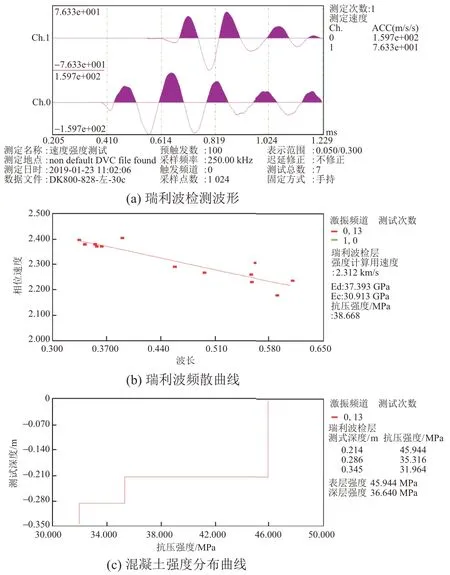
图7 瑞利波检测

由图7（c）可见，距表面21 cm 内混凝土强度为46 MPa，21～29 cm范围混凝土强度为35 MPa，而29 cm以上范围混凝土强度仅为32 MPa。衬砌表面附近混凝土强度较高，越往内强度越低，这与表面振捣工艺（如附着式振捣、高频平板振捣）有关。

3.1.3 检测参数

经过试验探索，铁路隧道衬砌混凝土（设计强度35 MPa）形状决定系数λ均在5.5 左右，而动弹性模量EA为38～41 GPa。为此，取省缺值39.5 GPa，综合钢筋率ρs取0.8%。

3.2 冲击弹性波法与取芯压载试验差异

由于检测区域、范围、深度及混凝土不均匀性等原因，取芯压载试验和无损检测方法之间必然有一定的区别，见图8。如瑞利波检测的标准测距为50 cm，芯样对测区的代表性仅有6.7%～13%。此外，对于结构检测，垂直于表面的裂纹对弹性波（特别是瑞利波）波速的影响较大，而取芯时常常会避开裂纹，其压载强度会大于检测强度。

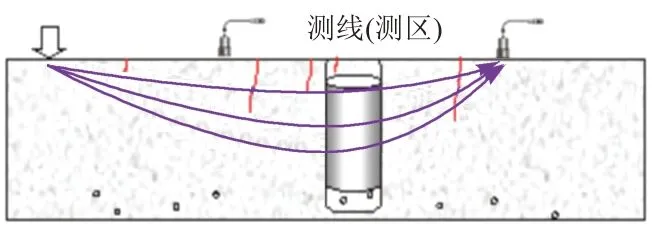
图8 测线（区）与芯样的区别

某铁路取芯压载与无损检验对比见表4和图9，取芯压载与无损检测结果的趋势一致，均值也比较接近，但两种方法都有一定离散，且其离散程度也相近。

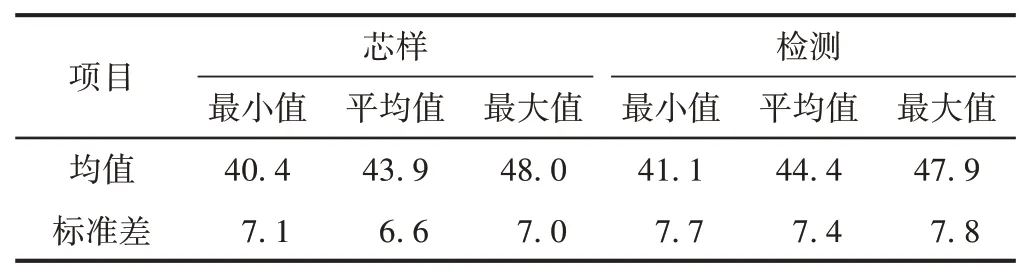
表4 取芯压载与无损检测试验对比 MPa

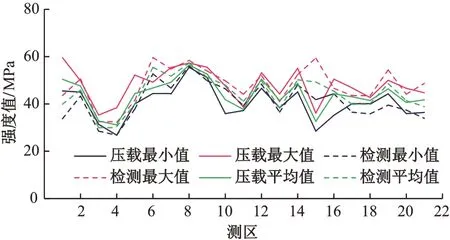
图9 各测线（区）强度值比较

3.3 验证结果

对145 个测区进行对比验证，见表5 和图10。期间，检测技术也随着现场验证的积累和深入而不断完善，后期与初期（测点47 之前）相比，检测精度有了明显提高。

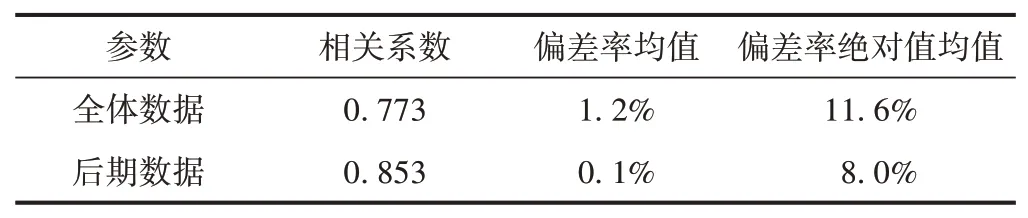
表5 混凝土强度检测结果统计

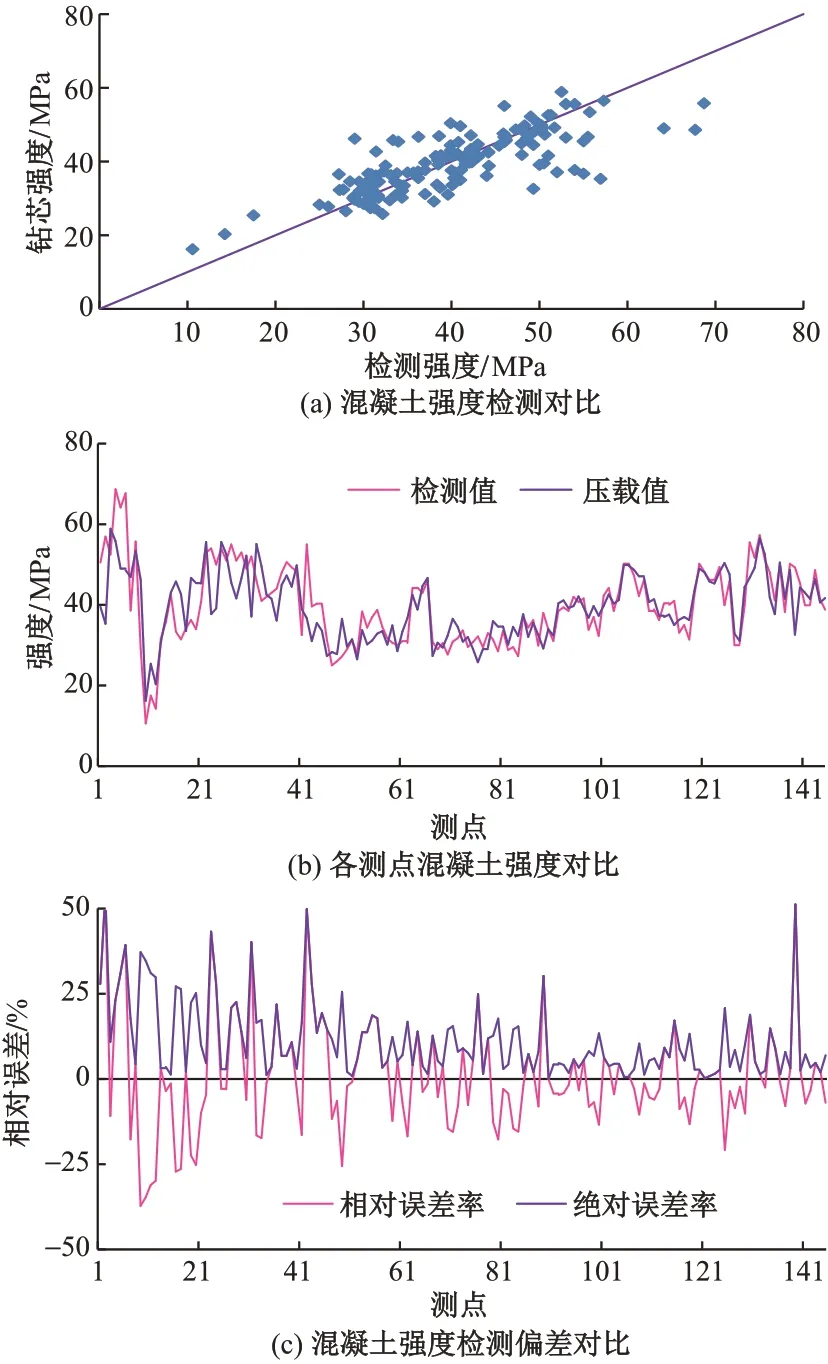
图10 混凝土强度检测结果对比

4 结论

本文通过对冲击弹性波理论的系统化研究，开发了针对混凝土强度的检测体系，具有如下特点。

1）检测精度高。无损检测结果与取芯压载结果的相关系数达到0.85，平均偏差率约8%（约3 MPa）。

2）功能齐全。不仅可推算混凝土抗压强度，还可精确检测混凝土动弹性模量。同时，还可以检测混凝土不同深度的弹性模量和抗压强度。

3）检测盲区少、适用范围广。不仅可以检测铁路隧道衬砌，还可以检测桥梁、房屋等各类混凝土结构。

与传统方法（如回弹仪法、超声回弹综合法等）相比，该检测方法无论在检测精度还是适用范围等方面均有较大进步。同时，仍存在一些需要改进之处，在以后的应用中应加强改良和完善，为我国土木工程行业质量、安全保障做出更大贡献。