一种适用于淤泥质底质的新型人工鱼礁的设计与研究
周秋萍,盛国强
(广州中国科学院工业技术研究院,广东 广州 511458)
人工鱼礁的建设对于保证海洋渔业增长,保护和改善海洋生态环境都有十分重要的作用[1-4]。传统的人工鱼礁主体均坐落在浅层有细砂覆盖的坚硬岩石质海床上[5-7]。在黏土、淤泥质和散沙上建造人工鱼礁还存在很大的困难,礁体投放后会发生整体沉降,最终导致礁体被淤埋[8-10]。但是在河流三角洲地区淤泥质软基分布较为广泛,且河口地区渔业资源丰富,珠江入海口目前投放的人工鱼礁容易被淤埋。本研究探讨了一种了能在淤泥质底质上保持稳定,不发生淤埋的人工鱼礁设计方法。
1 新型人工鱼礁及投放区域概况
1.1 新型人工鱼礁
新型人工鱼礁主要包含3部分结构:鱼礁本体、浮力基础和筒形桩(图1)。通过在传统人工鱼礁下方安装带筒形桩的浮力基础,可确保礁体投放后在淤泥基础上不发生埋淤,也不会因风暴潮作用而滑移、拔起。
浮力基础为中空密封结构,可以提供主动上浮力,当基础在泥面上时提供向下净重,当基础沉到泥面以下一定程度时,提供向上浮力,而且其浮力可以调整,基础越往下,其浮力越大,这样可以防止鱼礁持续下沉,具有一定的恢复能力。筒形桩安装完成后,对人工鱼礁坐底稳定有重要作用。首先,对于地基的竖向承载力而言,除了提供抗拔力外,桩身顶板还提供了稳定的淤泥承载力,桩径越大,所承受的竖向荷载力越大;其次,可承受较大的水平推力,提供较大的抗倾覆力矩。

图1 新型人工鱼礁示意图
用于后续分析的新型人工鱼礁的情况如下:筒形桩为钢质材料,直径0.159 m,壁厚4.5 mm,中心距2.0 m;鱼礁本体为混凝土材料,框型结构,规格为1m×1m×1m,棱柱宽0.13 m;浮力基础为混凝土材料,球冠状,球冠半径0.8 m,球冠高0.73 m,球冠壁厚65 mm。浮力基础内有间距为0.35 m的立柱十字布置。
1.2 投放区域
广州市南沙区地处珠江口与伶仃洋的交汇处,属于冲积平原,地表主要为第四纪沉积物,地层中存在深厚海陆交互相淤泥。根据综合调研结果及原位测试试验数据,投放区域的设计不排水抗剪强度值取7.0 kPa。人工鱼礁投放海域水深h=5 m。鱼礁坐底处潮流[11]:涨潮流向北北西约340°,落潮流向南南东约165°,主流与伶仃巷道走向一致,平时涨潮平均流速为0.2~0.4 m/s,落潮平均流速为0.3~0.5 m/s。风暴潮期间的最大流速为1.44 m/s。该海域以风浪为主,常浪向为东南偏南(SSE),频率15.3%,年平均波高0.2 m,最大波高1.92 m,最大平均波高0.68 m,平均周期3.5 s[12]。由于波周期的平方遵循瑞利分布,推算设计最大波周期4.55 s。
2 环境载荷评估
2.1 极限波浪载荷计算
人工鱼礁礁体设计,水深取5 m。根据文献[13]进行极限波流荷载计算:
(1)确定波长L。根据波浪的弥散关系计算波长L。

(1)

计算得到波长L=26.68 m。
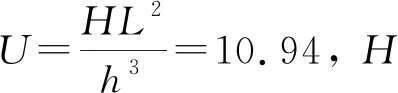
综上,波浪理论采用Stockes波理论。
(3)求解一定水深下的波速。水体内任意一点(x,z)水质点在任意时刻t(s)的水平流速u(m/s)和垂向流速w(m/s)。x,z的单位为m。
(2)
(3)
式中:ch、sh为双曲余弦和双曲正弦函数。
由式(2)、(3)计算得到不同水深下的最大水平和垂向流速(图2)。

图2 不同水深处最大流速分布
(4)求解人工鱼礁礁体在波浪和潮流的共同作用下的流速及作用力[14]。流速u是潮流速度u0(m/s)和波浪速度u1(m/s)合成的,即:
u=u0+u1
(4)
u1根据式(2)改写为:
u1=um1cosθ+um2cos2θ
(5)
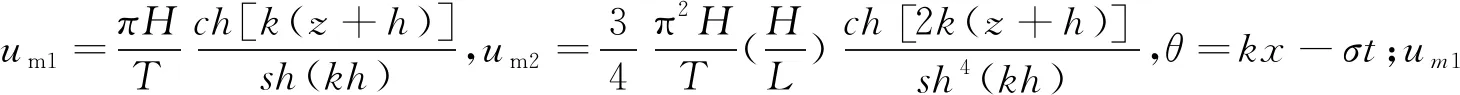
人工鱼礁礁体在流速u下的流体作用力可分成拖曳力和附加质量力,在数学形式上表示成流速与流速导数的函数,具体计算公式为:
(6)
式中:Cd为拖曳力系数;CM为附加质量系数;ρ为海水密度(1 025 kg/m3);A为迎流面积,m2;V为实体体积,m3。Cd、CM的值根据波浪KC数确定,KC数(Keulegan-Carpenter number)是一个无量纲数,用来描述一个在振荡流场中的物体,所受到的黏性力相对惯性力之间的关系。
将公式(5)代入公式(6),整理得到下式:
F=Fd(1+αcosθ+βcos2θ)2+FM(sinθ+2γsin2θ)
(7)
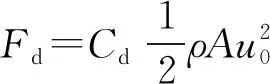
若要使得F取得最大值,需满足:
(8)
公式(7)、(8)中的各参数的实际取值以及最终求得作用在鱼礁及浮力基础水平波流计算见表1。

表1 鱼礁及浮力基础水平波流计算

2.2 Fluent仿真模拟
图3为数值模型计算区域,以鱼礁底面中心为坐标原点建立三维水槽,水槽长度足够可以保证水流达到鱼礁附近时趋于稳定,并满足尾流区的范围是10倍模型边长以上的要求[15]。计算采用Fluent中的VOF物理模型,进口边界采用速度及二阶stock波的进口边界条件设置,其中,造波边界设置可参考文献[16]。流场中鱼礁附近的流速分布如图4所示、动水压分布如图5所示。
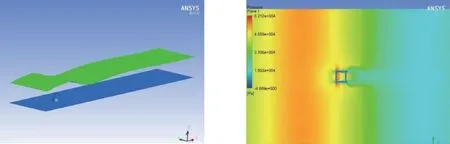
图3 鱼礁及浮力基础模型 图4 流速分布

图5 动水压分布
2.3 仿真和理论计算值对比
通过仿真分析和理论计算得到人工鱼礁上的水阻力和升力,人工鱼礁设计选用的环境载荷取两者较大者,仿真和理论计算结果对比见表2。
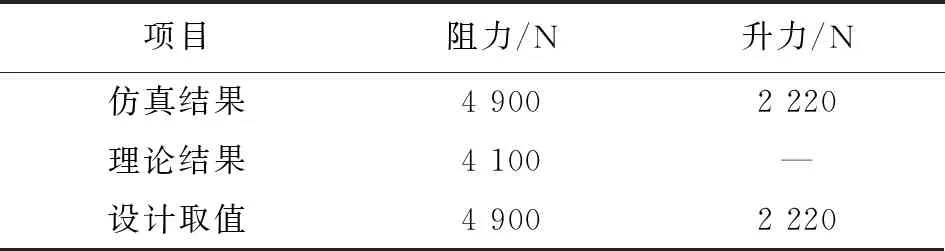
表2 仿真和理论结果对比
对于本研究中的鱼礁升力计算暂无理论计算的公式,故只进行了仿真分析。表2可以看出,鱼礁阻力计算仿真和理论计算结果较为接近,但偏大于理论值,这是符合实际的。理论计算基于势流理论,而仿真考虑了水体绕流产生的漩涡对结构的作用,之所以仿真值大是因为增加了部分的压差阻。
故阻力值选取了更偏于实际的仿真计算的结果值,即阻力4 900 N,升力2 220 N。
3 鱼礁强度分析
浮力基础及人工鱼礁所用材料为混凝土C40,其设计抗压强度为19.1 MPa;设计抗拉强度为1.71 MPa[17];矩形截面结构抗剪强度与抗压强度比值为0.065~0.089,取0.065,则矩形截面C40的设计抗剪强度为1.24 MPa。
浮力基础底板上受到的载荷:5 m水深的水压50 kPa,鱼礁坐底后连接钢架给底板的载荷(结构浮重)。边界条件如图6所示,浮力基础底板第一主应力云图如图7所示。从结果可看出,浮力基础底板第一主应力最大值为1.435 MPa,小于设计值,满足强度要求。

图6 浮力基础底板边界条件

图7 浮力基础底板第一主应力云图
浮力基础球壳及人工鱼礁上所受的载荷:人工鱼礁上所受极限海况的水动力,浮力基础受到极限海况的水动力,浮力基础受到的静水压力,自重载荷。边界条件如图8所示,浮力基础球壳及鱼礁第一主应力云图如图9所示。

图8 浮力基础球壳及鱼礁边界条件
从结果可看出,浮力基础球壳及鱼礁第一主应力最大值为0.721 MPa,小于设计值,满足强度要求。
4 抗淤埋分析
人工鱼礁安装稳定位置平衡方程为:
(ρ混-ρ水)gV鱼礁+(ρ材-ρ泥)gV桩+ρ混gV基础混-ρ水gV基础水-ρ泥gV基础泥=pAT
(9)
式中:AT为筒形桩底面积,m2;p为淤泥承载力,Pa;ρ混为混凝土密度,kg/m3;ρ材为筒形桩密度,kg/m3;ρ水为水的密度,kg/m3;ρ泥为淤泥的密度, kg/m3;V鱼礁为鱼礁体积,m3;V桩为筒形桩的体积,m3;V基础混为浮力基础混凝土体积,m3;V基础水为浮力基础在安装的平衡位置时排开水体积,m3;V基础泥为浮力基础在安装的平衡位置时排开泥体积,m3。
不考虑淤泥的承载力,安装稳定位置为泥面距离浮力基础顶部0.55 m处。该浮力基础埋在淤泥里一定深度,其浮力可以调整,基础越往下,其浮力越大,这样可以防止鱼礁持续下沉,具有一定的回复能力,起到抗淤埋的作用。
5 稳定性分析
5.1 分析方法
5.1.1 风暴潮作用下抗滑稳定性分析
根据《港口工程桩基规范》[18],桩的水平承载力可由下式确定:
FC=9CuD(L桩-1.5D)
(10)
式中:FC为单桩阻滑力,kN;Cu为不排水抗剪强度,kPa;L桩为桩的入土深度,m;D为筒形桩直径,m。
5.1.2 风暴潮作用下抗拔承载力分析
在黏土中,筒形桩考虑3种不排水破坏的模式:(1)桩单独从土中拔出;(2)桩内的土柱因张力失效而与基础分离和桩筒一同被拔出;(3)移动了大量土体,逆荷载失效,外部破坏。吸力桩的极限抗拔能力取3种所得的最小值[19-20]。
(1)桩单独从土中拔出,桩筒的内、外壁的土发生剪切破坏,其受力图如图10(a)所示,极限抗拔力为:
F1=WP+Fext-Fint+Te+Ti-Ftip
(11)
式中:WP为筒桩自身在淤泥中的浮重,kN,这部分在此由浮力基础抵消为0;Fext为桩顶外压力(kN),其中,Fext=Aeγwd1,Ae为桩顶外截面面积(m2),γw为水浮容重(kN/m3),d1为桩顶所处的水深(m);Fint为桩顶内压力(kN),其中,Fint=AiPtop,Ai为桩顶内截面积(m2),Ptop为桩内水压力(kPa);Te为外侧摩阻力(kN),其中,Te=PeCuAeL桩,Pe为桩截面外周长(m),Cu为不排水抗剪强度(kPa),L桩为入土深度(m),Ti为内侧摩阻力(kN),其中,Ti=PiCuAiL1,L1为桩内入土深度(m),Pi为内测周长(m),Ae、Ai根据API-RP-2GEO[21]第8.1.3节规定,对于欠固结黏土取1;Ftip为桩尖压力,其中,Ftip=Ptip(Ae-Ai),Ptip为基准水平面上桩截面 (土塞 )中的孔隙压力(kPa),当桩与土的界面完全空化Ptip=Ptop=-100 kPa(一个大气压),Ae≈Ai,Ftip约为0。
(2)当负压超过一定限制时,筒体及其土塞一块拔出,其受力情况如图10(b)所示,极限抗拔力为:
F2=Wp+Fext+Te+Ws+FT
(12)

(3)外部破坏情况,其受力情况如图10(c)所示,极限抗拔力为:
F3=Wp+Fext+Te+Ws+NCuAe-qtipAe
(13)
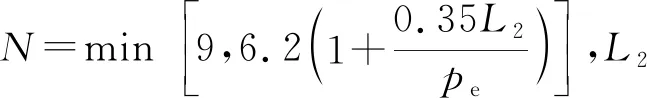
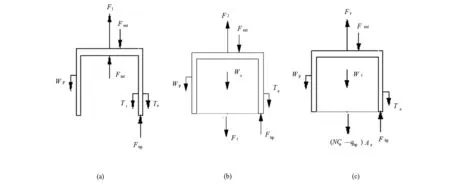
图10 筒形桩3种破坏模式受力图
5.1.3 风暴潮作用下抗倾覆稳定性分析
人工鱼礁礁体在水流和波浪的冲击作用下不发生翻滚倾倒,就需要满足筒形桩在埋置土中时其侧摩阻力和抗拔力共同作用下的力矩M1大于流体最大作用力产生的倾覆力矩M2。为了简化计算,将筒形桩的桩底作为旋转中心,且不考虑土体对筒形桩的土压力,抗倾覆的计算简图如图11所示[22]。

图11 人工鱼礁抗倾覆计算简图
M1=(F+Te)×L
M2=FH×H+FV×L/2
(14)
式中:M1为抗倾覆力矩,kN·m;M2为倾覆力矩,kN·m;Te为筒形桩周围土侧摩阻,kN;F为筒形桩抗拔力,kN;FH为波流水平力,kN;FV为波流垂直作用力,kN;H为水平力到旋转中心的距离,m;L距为筒形桩的中心距,m。自重未考虑的原因是自重与浮力基础产生的浮力相互抵消,垂向合力为0。
5.2 稳定性校核
水平抗力FC=14.5 kN。波流联合作用的水平冲击力FH=4.9 kN。计算得到抗滑系数为14.5/4.9=3.0,满足规范要求[23]。
根据破坏模式不同分3种情况进行计算,失效模式1、2、3算得的竖向抗拔力分别为17.3 kN、16.3 kN、13.5 kN,抗拔承载力取最小者。波浪产生的上托力FV=2.22 kN,故设计的筒形桩的抗拔系数为13.5/2.22=6,满足规范要求。
计算得到M1=62.4 kNm,M2=12.0 kNm,抗倾覆系数为62.4/12=5.2,满足规范要求。
6 结论
针对淤泥质地质条件,设计了新型的人工鱼礁,以确保鱼礁不淤埋,并根据波流动力学理论及Fluent数值模拟对此礁体进行稳定性计算,结果表明,在波流作用下,礁体最大作用力为4 900 N,最大作用力矩12 000 Nm,抗滑系数3,抗拔系数6,抗倾覆系数5.2,满足礁体稳定性要求。
□

