40Cr钢软化退火态抗拉强度检测数据的不确定度分析

马骁飞1，殷俊林

(1.同济大学第一附属中学，上海 200438；2.同济大学材料科学与工程学院，上海 200092)

0 引言

测量过程中存在许多不确定因素。一般情况下的测量，通过采用多次重复测量得到平均值的方法来提高测量值的可信度。但对要求高的测量，这样的测量结果是不符合要求的，需要了解有哪些主要因素影响测量过程，得到的最终测量结果的可信度又是多少。

1963年，原美国标准局的数理统计专家艾森哈特在研究“仪器校准系统的精密度和准确度估计”过程中，提出了采用“不确定度”的概念，受到国际上的普遍关注。

1980年，国际计量局在征求了32个国家的国家计量院和若干个国际组织的意见后，发出了推荐采用测量不确定度来评定测量结果的建议书。如今测量不确定度的国际标准和中国国家计量技术规范已经实施多年，不确定度已经成为国内和国际间评定测量结果的一种统一而且定量的指标。

测量不确定度理论认为被测对象的真值是客观的，但是由于系统误差和随机误差，无法知道真值的确切大小，故实际检测所得的数值只是一种估计值，可以通过合理的分散区间来表示被测对象的真值分布于其中的可能性。

1 测量不确定度的表达

在国际标准和我国的计量技术规范中，对测量结果不确定度的表达方式有各种具体规定。实际应用过程中，可根据检测对象、试验要求等不同情况,选择相对最佳的表达形式。

本文选用一种较为典型、简洁的测量不确定度表达形式，如式(1)所示：不确定度被表示为一个区间，即被测量之值X落在(X±U)区间中的概率为P。

X=X±U,P

(1)

式中：X为被测量之值，X为被测量之值的平均值，U为被测量之值的不确定度，P为置信概率。

通过这种表达方式，可以较为直观地判断某测量结果的可靠性。在实际应用与标准规范中，通常选择P为95%置信概率水平的不确定度数值。当然，某些情况下，也可以选择其它置信水平的不确定度数值，比如判断仪器的测量准确度是否可以接受时，P为99%置信概率的测量不确定度数值应用较多。

2 40Cr钢软化退火态的抗拉强度试验

本文参照《JJF1059.1-2012 测量不确定度的评定与表示》，对40Cr钢经软化退火处理后的抗拉强度数据进行不确定度分析和评定。为便于计算，采用相对不确定度方案，即评估所得的不确定度为相对量，无单位，即相当于式(1)中的U/X。

拉伸试验按《GB/T228.1-2010 金属材料拉伸试验 第1部分：室温试验方法》进行，试样采用图1所示的圆棒型。

抗拉强度的数学模型，即计算公式如下：

(2)

式中：Rm为抗拉强度，MPa；Fm为最大拉伸力值，N；d0为试棒标准距离区域的横截面直径，mm。

本次抗拉强度测试试样为15件，采用3种不同的加载速度进行测试，并按式(2)对获得抗拉强度的测试结果进行处理，结果如表1所示。

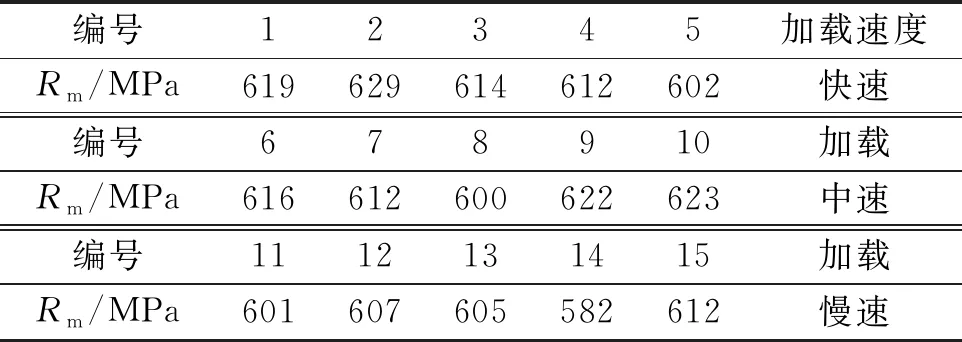
表1 40Cr钢抗拉强度Rm实测值

3 抗拉强度实测值的不确定度来源

测量不确定度由多个分量组成，实际工作中不可能、也没有必要识别并计算出所有分量，较为合理并可行的做法是识别出有显著贡献的不确定度。其中一些不确定度分量可以通过测量结果的统计分布估算，并用试验标准差表征。另一些不确定度分量则可以采用基于经验或者其他信息的假定概率分布估算，也可以用标准差表征。

从(2)式所示的数学模型可见，抗拉强度的测量不确定度主要来自试验机力值系统误差与试样截面积测量误差；此外，检测的重复性及试验加载速度的影响也可能有较明显贡献。可用鱼刺图的形式较为直观地呈现抗拉强度检测值的不确定度来源情况，如图2所示。

4 抗拉强度的不确定度评定

针对表1中所列出的抗拉强度实测值，进行不确定度评定。

4.1 抗拉强度

对于因重复性检测产生的测量结果相对不确定度分量，可采用统计分布的方法估算。计算出抗拉强度值的标准差和均值，两者之比为相对标准差，即为重复性检测产生的测量结果相对不确定度如式(3)所示：

(3)

式中：urel(rep)为抗拉强度重复性检测结果的相对不确定度分量，Rm,i为抗拉强度的第i次测量值，Rm为抗拉强度n次测量值的平均值，n为测量次数，本文n为15。

经计算，urel(rep)为1.77% 。

4.2 试样截面面积测量引入的相对不确定度

urel(S0)=2urel(d)=2a/k

(4)

式中：urel(d)为“试样截面直径”测量引入的相对不确定度分量。

经计算，urel(S0)为0.58% 。

4.3 试验加载速度引入的相对不确定度

urel(v)=a/k

(5)

经计算，urel(v)为2.22% 。

4.4 试验力值系统引入的相对不确定度

从图2所示的抗拉强度不确定度来源鱼刺图可见，试验力值系统相对不确定度分量urel(F)包括3个方面：(1)试验机测力；(2)试验机力值采集；(3)试验机力值校准。

4.4.1 试验机测力的相对不确定度

urel(F1)=a/k

(6)

经计算，urel(F1)为0.29% 。

4.4.2 试验机力值采集的相对不确定度

查询试验机有关技术资料得知，此次试验所用试验机的数据采集频率为2.5 kHz，数据准确度高，偏差不大于0.1%，故取偏差上限作为试验机力值数据采集的相对不确定度urel(F2)，即urel(F2)为0.10% 。

4.4.3 试验机力值校准的相对不确定度

urel(F3)=a/k

(7)

经计算，urel(F3)为0.06%。

4.4.4 试验力值系统各相对不确定度子项的合成

通过4.4.1～4.4.3节分别评估，得出了试验力值系统中3个相对不确定度子项，按式(8)可计算得出这3项不确定子项的合成标准不确定度urel(F)，即为试验力值系统的相对不确定度分量：

(8)

经计算，urel(F)为 0.31% 。

4.5 抗拉强度的合成不确定度

通过4.1～4.4节分别评估，得出了构成抗拉强度检测结果相对不确定度的4个主要组成部分：(1)重复性检测引入的相对不确定度urel(rep)、试样截面面积测量引入的相对不确定度urel(S0)、试验加载速度引入的相对不确定度urel(v)、试验力值系统引入的相对不确定度urel(F)，按式(9)计算出这4个主要相对不确定度分量的合成相对不确定度urel(Rm)：

(9)

经计算，抗拉强度的合成相对不确定度为2.91%，根据正态分布原理，取包含因子k=2，则得出此次试验检测所得的40Cr钢抗拉强度数值在置信概率(又称包含概率)95%的扩展相对不确定urel(Rm)为：

urel(Rm)=kurel(Rm)

(10)

经计算，urel(Rm)为5.82%。

如前所述，为了便于计算，本文采用了相对不确定度方案进行评估。至此根据得到的扩展相对不确定度urel(Rm)，乘以抗拉强度的均值即可获得扩展不确定度U(Rm)：

U(Rm)=urel(Rm)×Rm

(11)

经计算，U(Rm)约为36 MPa。

此次40Cr钢软化退火态抗拉强度检测数据的不确定度可表示为：

Rm=(612±36) MPa，P=95%

即抗拉强度处于(612±36) MPa区间的置信概率为95%。

5 结论

本文是测量结果不确定度分析方法在金属材料室温拉伸试验中的一次具体应用，分析结果有助于定量判断试验数据的可靠性或可接受程度。

该方法也可广泛适用于评估科学试验中所得的检测数据。在使用过程中，需要仔细梳理主要的不确定度来源，充分利用统计方法和各种经验数据，以尽可能提高测量结果不确定度分析的精确性。