运动船舶LNG 分层翻滚过程熵产分析

甄阳阳，卢金树，朱正褀，袁世杰

(浙江海洋大学船舶与海运工程学院，浙江舟山 316022)

LNG 船舶在海上航行过程中，液舱内LNG 通常会因老化(氮元素或者轻质组分的优先蒸发)行为出现密度及温度不同导致的液体分层现象；同时，又因为舱壁漏热与海上风、浪、流等因素的共同作用，影响分层状态的LNG 流动，极易导致舱内LNG 发生翻滚现象。当舱内分层液体发生翻滚时，液舱下层过热液体与上层较冷液体发生混合释放大量的热量，与此同时产生大量LNG 蒸气，气相空间的瞬间冲击力对LNG液舱性能及安全性有较大影响，威胁LNG 船舶的安全航行过程。因此，当液舱内LNG 处于分层状态的船舶在海上航行时，液舱内分层液体受舱壁漏热与船舶运动的共同影响，两者对LNG 分层翻滚的作用将会耦合，加剧舱内分层LNG 的流动变化，影响其分层翻滚过程[1]。

近年来大量学者对静止储罐内翻滚过程气液界面处的热、质传递过程进行研究[2]，得出不同外界条件及初始条件对LNG 翻滚的时刻与持续时间的关系[3]。有学者分别对静止与运动状态下的LNG 船舶进行分层翻滚数值模拟研究，得出在运动条件与静止条件下LNG 密度趋于一致性的主要因素分别是运动动力与热量导致的自然对流[4]。综上所述，目前学者对静止容器中LNG 分层翻滚过程研究较多，但多基于特定情况进行数值模拟，得出的结论不具有一般性。故本文从热力学熵产角度去分析LNG 分层翻滚过程，将不同边界条件与初始条件通过熵产这一参数进行统一化。同时船舶运动影响舱内LNG 分层翻滚过程，而学者对处于运动工况下船舶LNG 分层翻滚过程研究较少，故本文以船舶不同运动强度为研究因素对LNG 分层翻滚过程进行熵产分析。

本文对LNG 船舶运动工况下的分层翻滚过程进行数值模拟研究，以LNG 液舱为研究对象，基于mixture 模型与标准方程模拟LNG 液舱内分层翻滚过程；通过计算得出液舱内流体速度场及温度场，对LNG液舱分层翻滚过程进行熵产计算及特性分析，基于熵产理论分析LNG 船舶在不同运动状态下的分层翻滚过程，探究LNG 分层翻滚过程的晃荡效应。

1 LNG 分层翻滚现象描述

静止船舶LNG 分层翻滚过程实质上是由于在罐壁传导的热量引起罐壁处液体密度发生变化，导致罐壁处液体浮升力变化引发流动[5]。对储罐内分层LNG 进行热流动分析，可更好理解LNG 从分层到翻滚的演变历程。如图1 所示为LNG 分层自然对流示意图。

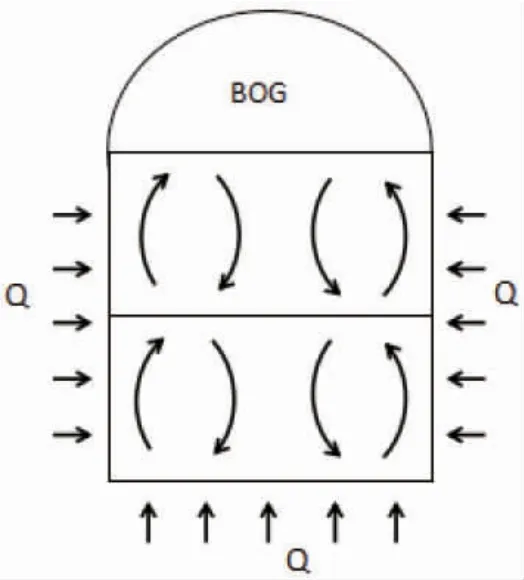
图1 LNG 分层自然对流示意图Fig.1 LNG stratified natural convection diagram

LNG 储罐中形成稳定分层是因为上层液化天然气的密度较小，温度较高，下层液化天然气的密度较大，温度较低。伴随着储罐与外界进行热量交换，罐内LNG 温度上升，导致下层LNG 密度减小，沿罐壁向上流动，与上层LNG 热、质交换，下层LNG 在层内向舱壁中心处水平流动，与其他侧壁处下层LNG 相互混合，沿储罐中心线向下流动，在储罐下层形成自然对流循环；由于上层LNG 所吸收热量主要来自罐壁与下层LNG 液体，上层LNG 密度逐渐降低，浮升力增大，故沿着罐壁向上流动，一部分LNG 在气液分界面处通过蒸发向气相空间传递一部分热量，剩余部分流体沿储罐中心处向下流动，由此形成上层LNG 自然对流循环。在无循环泵等外力因素打破这种层内自然对流的情况下，LNG 储罐内的分层状态会随着罐壁热量的持续进入而达到一个翻滚临界点—即上层与下层LNG 密度趋于相同，导致翻滚现象出现。

2 模型建立

2.1 物理模型

本文为模拟海上LNG 液舱分层翻滚过程，研究舱内流体流动熵产及传热熵产变化特征，取某5 000 m3LNG 液舱为研究对象，构建如图2 所示LNG 液舱二维模型[4]，物理模型几何参数为b=20 m，h=15 m，h1=3 m，h2=2 m。

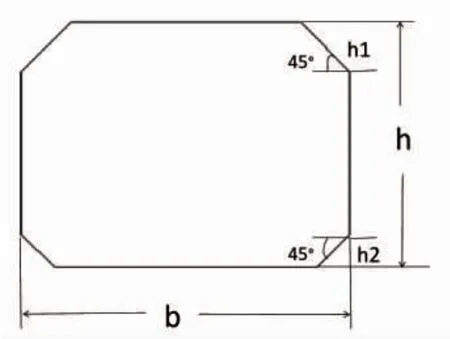
图2 液舱二维模型尺寸图Fig.2 Dimension diagram of two-dimensional tank model

由于本文主要研究液舱内分层流体翻滚情况及熵产特性，因此忽略舱壁结构及模型舱壁厚度，不考虑受船舶海上运动时由于舱内液体晃荡造成的舱壁结构变形。

本文将LNG 简化为单一甲烷组成，其物性参数随温度变化如表1 所示[6]。在数值模拟中采用表1 中LNG 物性参数，分为上下两层，取上层LNG 温度为111 K，密度为423.33 kg·m-3，下层LNG 温度为110 K，密度为424.78 kg·m-3，上下层液体高度均为7.5 m。

表1 甲烷物性参数与温度的关系Tab.1 Relationship between physical parameters and temperature of methane

LNG 物性关联式表示LNG 均处于饱和状态，故可忽略液舱气相空间与LNG 相变过程，只取液相来研究LNG 液舱分层翻滚过程。

2.2 数值模型

在满足计算问题要求的前提下，设置合适的求解策略对提高计算效率及精度显得尤为必要。

(1)网格划分

运用CFD 前处理软件对LNG 液舱物理模型进行建模，采用四面体结构性网格进行网格划分，边界层进行加密处理，取网格数量为43 434，节点数为43 014，网格模型经无关性验证。

(2)边界及初始条件

本文主要模拟分层及翻滚过程，忽略顶部气相空间，针对已分层液体区域进行计算，边界设置为固壁面条件，侧壁与底部设置相同漏热强度(30 w·m-2)，顶壁设置为绝热条件。初始化温度：上层液体110 K，下层液体111 K，因其密度与温度呈线性关系，故LNG 液舱内上层LNG 密度设定为423.33 kg·m-3，下层LNG 密度设定为424.78 kg·m-3。初始条件取u=0、v=0，k 和ε 都保持默认值。

(3)数值方法

PISO 算法执行2 个额外的校正，临近校正和偏度校正，对于大时间步长瞬态计算，其精度较高。本文研究的LNG 液舱分层翻滚过程属于瞬态非定常问题，基于计算精度与经济性考虑，研究选用非定常算法PISO(Semi-Implicit Method Pressure Linked Equations)较为合适[7]，梯度离散格式选用Least Aquares Cell Based，压力离散格式为PRESTO，其余各部分离散格式选用First Order Upwind。时间步长选用0.01 s；松弛因子为默认值。

2.3 数学模型

通过对LNG 液舱分层翻滚过程数值分析，可获取二维大型LNG 液舱分层翻滚的质量方程、动量方程、能量方程、热传导方程、k 方程、ε 方程，通过查询相关文献，可得适用于LNG 液舱分层翻滚过程的熵产率及熵产方程[4]。

(1)质量方程：

(2)动量方程：

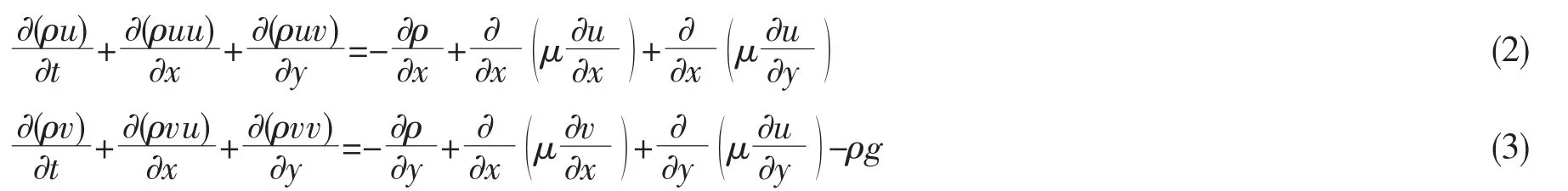
(3)能量方程：

(4)热传导方程：

其中ρ 为流体密度，kg·m-3；t 为时间，s；u、v 分别是X、Y 方向的速度分量，m·s-1；T 为流体温度，K；p 为压强，Pa；λ 为流体导热系数，W·m-1·K-1；q 为热流密度，W·m-2；Cp为流体定压比热容，J·kg-1·k-1。

(5)熵产率方程

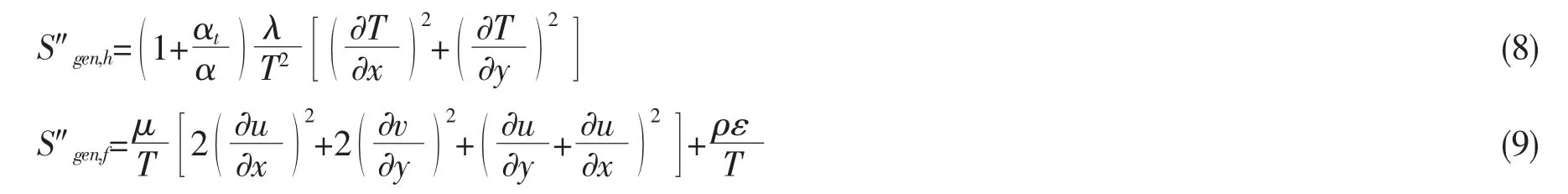
(6)熵产方程

将熵产率方程进行积分可得熵产方程[9-10]：

Sgen,h为传热熵产，W·k-1；Sgen,f为流动熵产，W·k-1；αt为湍流热扩散率，m2·s-1；α 为热扩散率，m2·s-1；λ 为热导率，W·m-1·K-1；μ 为动力粘度，Pa·s；ε 为k 的耗散率，m2·s-3；T 为液相温度，K；u、v 分别为X、Y 方向速度，m·s-1。

3 数值计算与结果讨论

3.1 运动船舶LNG 分层翻滚过程熵产特性分析

为研究船舶在运动工况下LNG 分层翻滚演变情况，将海上船舶非线性运动简化为正弦运动，通过设置不同运动周期及运动幅值对LNG 液舱分层翻滚过程进行研究，其运动周期及幅值取值范围如表2所示[8]。

表2 运动工况影响因素Tab.2 Influence factors of moving condition

3.1.1 运动幅值的影响

图3 为LNG 船舶不同运动幅值LNG 流动熵产时域图。当船舶处于定周期，变幅值的运动状态时，舱内流体流动熵产呈周期变化，且随着船舶运动幅值增大而增大；流动熵产值在同一周期内变化区间随船舶运动幅值增大而增大。

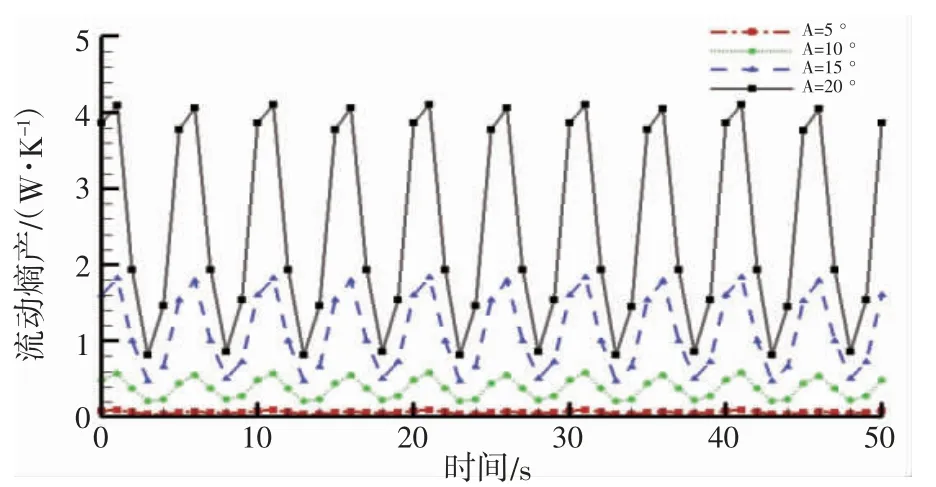
图3 流动熵产时域图Fig.3 Time history of flow entropy generation

图4 是船舶不同运动幅值LNG 传热熵产时域图。传热熵产时域图表示在LNG 分层翻滚过程中LNG能量随时间损失情况，在0 到500 s 时间内，流体传热熵产值减小速率较快，传热熵产值随船舶运动幅值增大而减小，其原因在于定周期下，运动幅值越大，其液相运动平均速率越大，液相温度趋于一致性速率越快，传热熵产减小速率随船舶运动幅值增大而增大。在500 s 之后，传热熵产减小速率减慢，传热熵产值随时间增大逐渐趋近于0，说明LNG 液舱内液体温度达到相同状态，其液相完全混合。

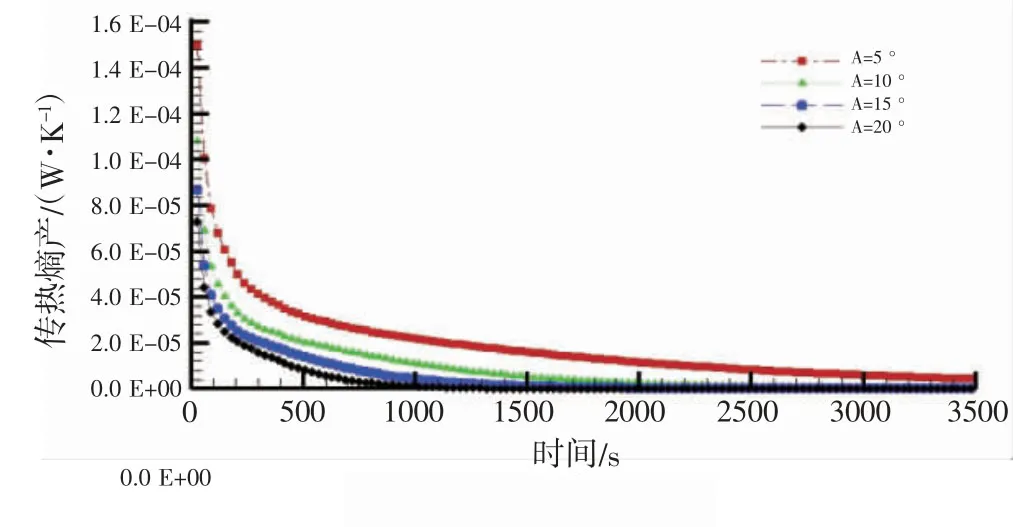
图4 传热熵产时域图Fig.4 Time history of heat transfer entropy generation

3.1.2 运动周期的影响

从图5 船舶不同运动周期LNG 流动熵产时域图可知，当船舶处于定幅值，变周期的运动状态时，舱内流体流动熵产呈周期分布，且随着船舶运动周期增大而减小；流动熵产值在同一周期内变化区间随运动周期增大而减小。

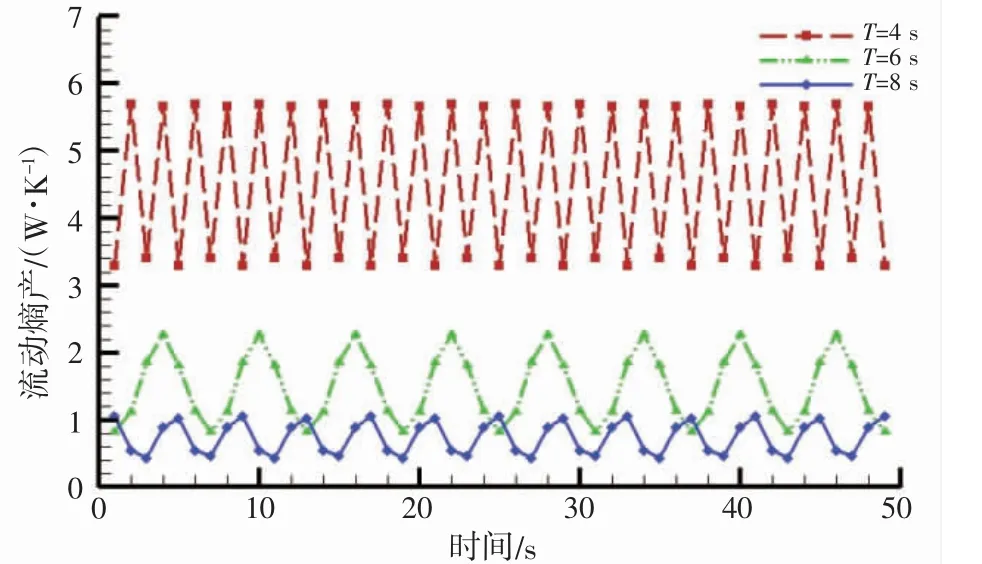
图5 流动熵产时域图Fig.5 Time history of flow entropy generation

从图6 船舶不同运动周期LNG 传热熵产时域图可知，在0 s 到500 s 时间内，传热熵产有较大的减小速率，传热熵产值随运动周期减小而减小，其原因在于定幅值下，运动周期增大，舱内液相混合速率越小，液相温度趋于一致性速率越慢，传热熵产减小速率随船舶运动周期增大而减小。在500 s 之后，传热熵产减小速率减慢，传热熵产值随时间增大逐渐趋近于0，说明LNG 液舱内液体温度达到相同状态，其液相完全混合。

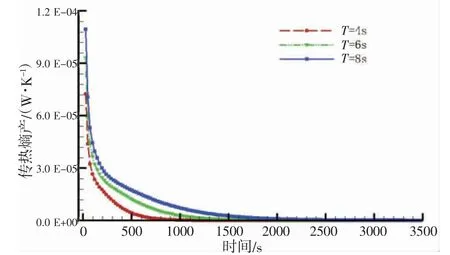
图6 传热熵产时域图Fig.6 Time history of heat transfer entropy generation

综上所述，当船舶处于运动状态时，液舱内流体流动熵产值呈现周期性变化，且随船舶运动强度增强而变大，船舶运动强度越强，舱内流体流动速率越大，流体流动损失越大。液舱内流体传热熵产值在0 到500 s 时间段有较大的减小速率，且随船舶运动强度增强而增大，在500 s 之前，液层之间、舱壁处液体与舱壁之间存在一定的温差，存在较大的传热熵产。在500 s 之后传热熵产以较小的减小速率逐渐趋于0，原因在于舱内液体温度逐渐趋于一致，舱壁处液体温度存在较小的温度梯度，故产生的传热熵产值随时间逐渐趋于0。

3.2 运动船舶LNG 分层翻滚过程熵产机理分析

3.2.1 运动幅值的影响

为进一步研究运动船舶LNG 分层翻滚过程熵产机理，本节对流动熵产率分布云图分析，如图7 所示为不同运动幅值时流动熵产率分布云图。图中流动熵产率大小表示LNG 分层翻滚过程中流体动量损失多少，通过了解LNG 分层翻滚过程中流体动量损失，可得知液舱内LNG 的流动状态。

由图7 可知，当A=15°时，初相位状态，液舱节点处与上下舱壁处存在较大流动熵产率；中相位状态，液舱节点处与左右舱壁处存在较大流动熵产率；左止点与右止点状态，舱壁处存在一定的流动熵产率。液舱内流动熵产率随运动周期呈现出初期减小，中期增大，后期减小的变化特征；流动熵产率在各个阶段主要分布于舱壁处，舱内流动熵产率分布较均匀，且处于较小值。

图7 流动熵产率分布云图Fig.7 The rate diagram of flow entropy generation

横向对比船舶不同运动幅值下LNG 流动熵产率分布云图，发现液舱流动熵产率的变化趋势不随船舶运动幅值发生变化；在每一运动阶段，流动熵产率随船舶运动幅值增大而增大。船舶在同一运动周期下，运动幅值越大，表示船舶运动强度越大，其舱内流体流动平均速率就越大，故产生的流动熵产率液随之增大。

3.2.2 运动周期的影响

如图8 所示为船舶不同运动周期下LNG 流动熵产率分布云图。由图可知，在船舶处于初相位时，液舱节点与上下舱壁处存在较大流动熵产率；在船舶处于中相位时，液舱节点与左右舱壁存在较大流动熵产率；在船舶处于左止点与右止点时，液舱舱壁处存在一定的流动熵产率，相对船舶处于初相位与中相位的流动熵产率要小。分析可知，船舶运动到初、中相位时，舱内流体流动速率达到最大值，舱壁处存在较大动量损失，存在较大的流动熵产率，在船舶运动至左右止点时，左右舱壁处液体速度方向转变，流体速率较小，故流动熵产较小。

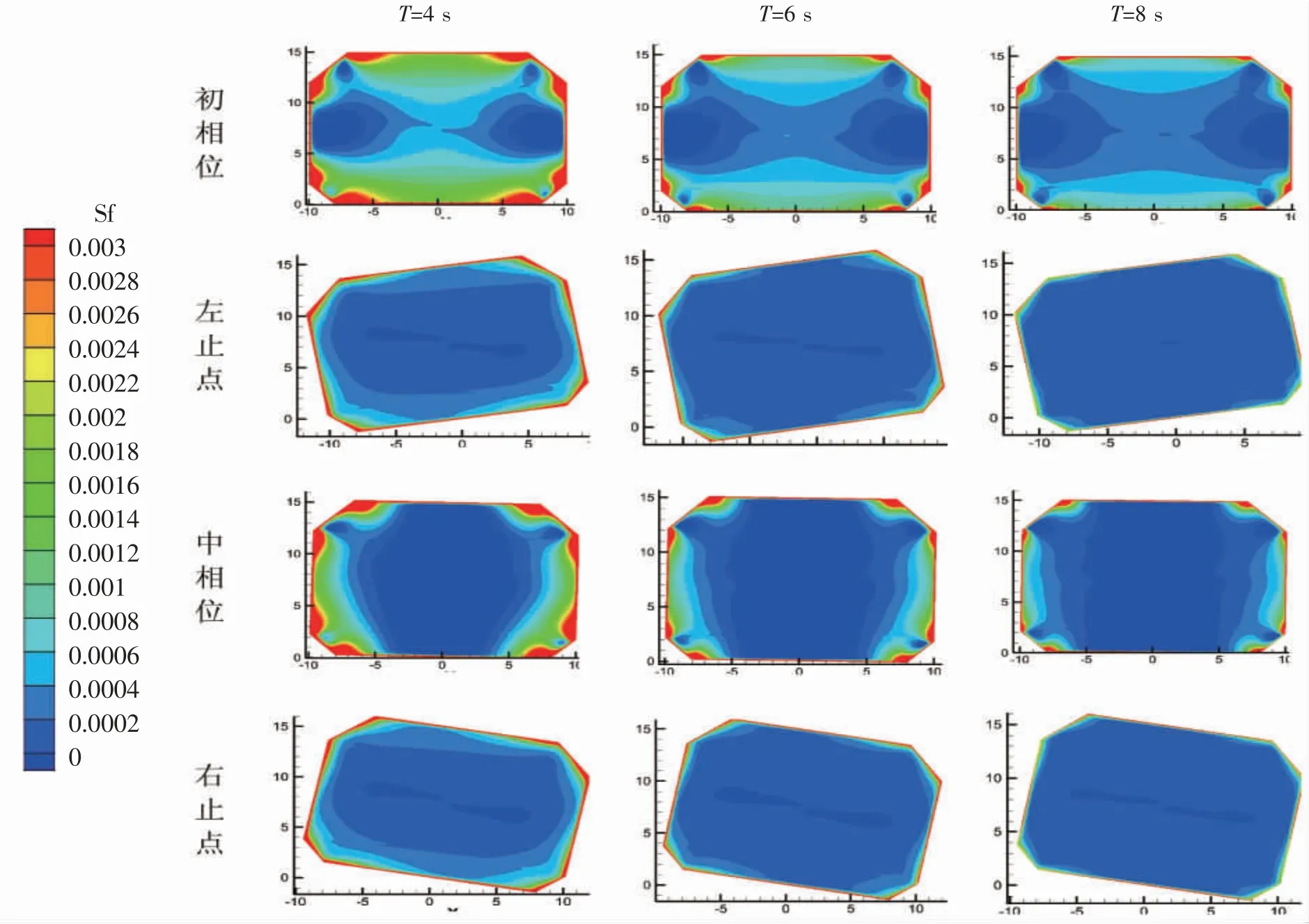
图8 流动熵产率分布云图Fig.8 The rate diagram of flow entropy generation

横向对比船舶不同运动周期下LNG 流动熵产率分布云图，发现液舱LNG 流动熵产率变化趋势不随船舶运动强度增大而发生变化；在每个阶段，LNG 流动熵产率随船舶运动周期增大而减小。船舶在同一运动幅值下，运动周期越大，表示船舶运动强度越小，舱内流体流动平均速率越小，产生的流动熵产率也随之减小。

综上所述，当船舶处于运动状态时，液舱内流体流动熵产率呈周期性变化，且随船舶运动强度增强而变大，船舶运动强度越强，舱内流体流动平均速率越大，流体流动动量损失越大。

4 结论

本文通过研究运动船舶LNG 分层翻滚过程熵产率及熵产值，以LNG 液舱为研究对象，探究LNG 分层翻滚过程中能量及动量损失情况，得到结论总结如下：

(1)当船舶处于运动状态时，液舱内流体流动熵产率及熵产值呈周期性变化，随船舶运动强度增强而变大。当船舶运动强度越强，舱内流体流动平均速率越大，流体动量损失越大。流动熵产率主要分布于舱壁处，表明舱壁处动量损失较大。

(2)液舱内流体传热熵产值在0～500 s 时间段有较大的减小速率，随船舶运动强度增强而增大。在500 s之前，液层之间、舱壁处液体与舱壁之间存在较大的温差，故在传热过程中有较大的能量损失。在500 s 之后传热熵产以较小的减小速率逐渐趋于0，原因在于舱内液体温度逐渐趋于一致，舱壁处液体温度存在较小的温度梯度，其传热过程中损失能量较少。