近几年云南省中学数学特岗教师考试试题分析与研究
卢 萍,张 露,李爱珍,施育凤,张朝元
(大理大学数学与计算机学院,云南大理 671003)
自2012年《云南省农村义务教育阶段学校教师特设岗位计划实施方案》〔1〕颁布以来,2016—2019年这4 年,云南省特岗教师在2016 年招聘了7 200人、2017年招聘了5 000人、2018年招聘了5 409人、2019 年招聘了6 090 人,4 年共招聘了23 699 人,其特岗教师竞争比例达到了13:1,由此可见中学数学特岗教师竞争激烈。目前对特岗教师考试方面的研究主要侧重于特岗教师的政策和未来的发展,且在这方面的研究上取得了一定的成果,但是对于特岗教师考试试题分析与研究的甚少。对此本文将通过收集整理2015—2018 年的云南省中学数学特岗教师考试真题,从试卷结构、考点内容、考点分值、高频考点和试题特点等几个方面来分析与研究。希望能够帮助备考的考生明确试题的考查特点,有条理、有目的地备考。
1 试卷结构分析
特岗教师考试的内容主要由专业基础知识与教育学心理学两部分构成,本文将从专业基础知识中的数学学科基础知识这一模块来对历年考试试题进行统计分析。近几年真题具体考查的试题题型及分值如表1所示。
从表1 中不难看出,近几年特岗教师考试的试题题型和分值分布基本稳定,都由选择题、填空题、简答题3 种题型所构成,共80 分占总分120 分的66.67%。其中选择题有10 个小题,每小题3 分,共30 分,占试卷总分的25.00%;填空题有6 个小题,每小题3分,共计18分,占试卷总分的15.00%;简答题有5 个大题,虽然2015 年与其他三年第20、21 题所占的分值有所变动,但简答题部分的总分都保持不变,都为32分,占试卷总分的26.67%。

表1 近几年特岗教师考试题量分布
2 考点内容分析
根据近几年试题的考点来看,数学学科基础知识是特岗教师考试的重点考查对象,主要考查考生在数学领域的基础知识。下面对各题考点做了分类整理,具体的考点分布见表2。
首先,从表2中不难看出,特岗教师考试中试题的考查范围较广,并且在每份真题中高中数学知识所考查的内容较多,基本上涉及了高中数学的所有知识。如:数列、向量、函数及其性质、导数、立体几何、复数、三角函数的性质与应用、解三角形、圆锥曲线、计数原理、概率统计等。
其次,从试题的重难点上来看,试题对大学数学知识中的极限、定积分、不定积分都进行了重点的考查;对高中数学知识中的函数与导数的应用、圆锥曲线、计数原理与概率统计、立体几何等进行了重点考查;对初中数学中的图形与几何、规律探索、数与代数也进行了重点考查。
最后,从试题的结构上来看选择题(第1—10题)、填空题(第11—16题)中有些考点每年都出现,如集合运算、平面向量、三角恒等变换、极限的计算、圆锥曲线的性质、函数与导数,然而这些都是数学的基础知识,可见特岗考试在重视能力考查的同时,也注重基础知识的考查;对于简答题(第17—21题)来说,明显地可以看出来它所考查的都是综合应用题,比如说圆锥曲线的应用、立体几何、导数的应用、数列的应用、概率统计、不等式的应用等,这些综合性较强的知识点,往往是特岗考试的重点和难点,这也是考验考生掌握知识的连贯性和分析问题的综合能力。
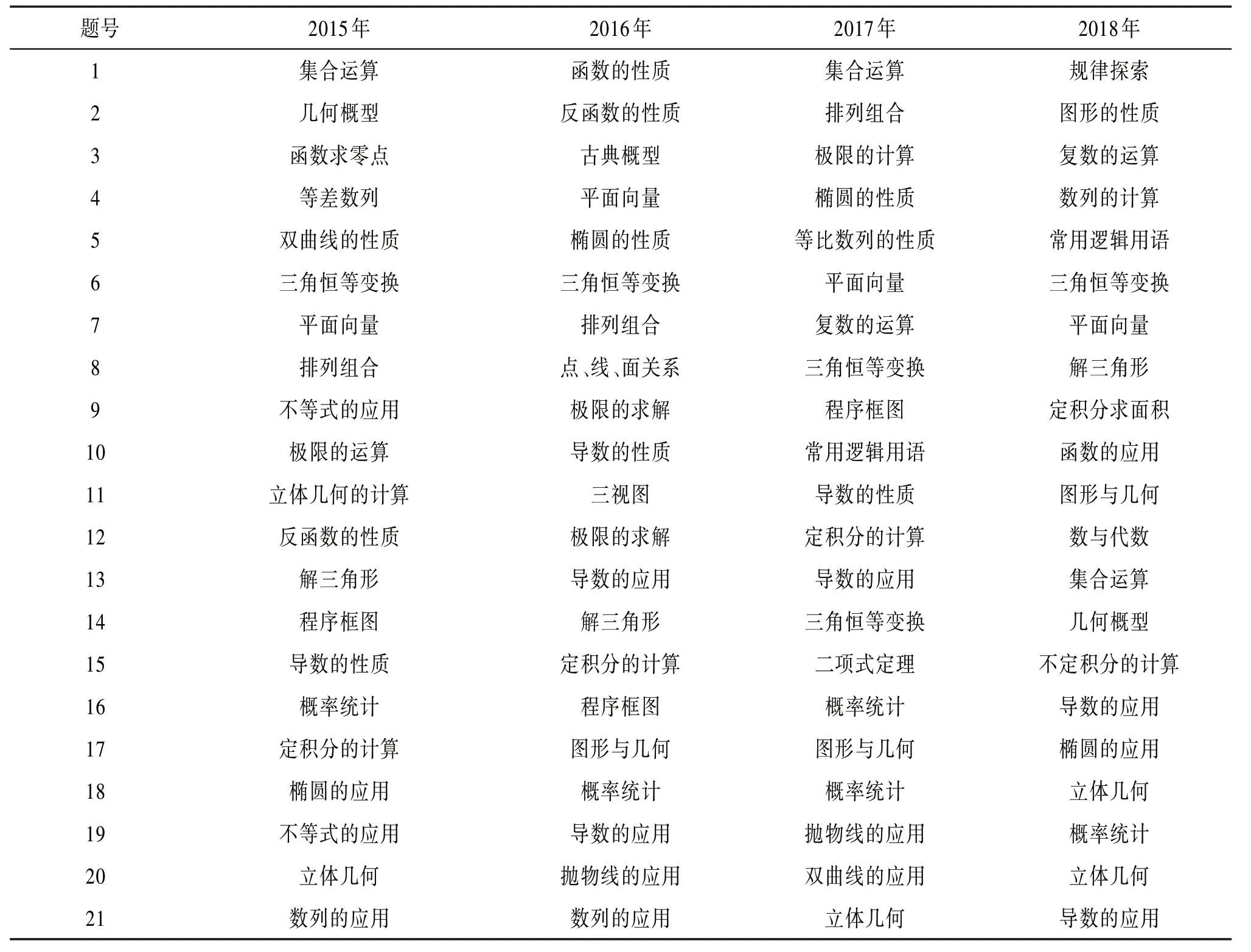
表2 试题数学学科基础知识考点分布
3 考点分值分析
基于表2 中的考点分布,可将考点主要分为集合与常用逻辑用语、函数与导数、三角函数与解三角形、平面向量、立体几何等12 个模块。每个模块的分值情况见表3。

表3 试题考点分值分布
从表3试题的考点分值分布上来看,首先,可以明显地看出函数与导数、计数原理与概率统计这两个模块所占的分值较高,函数与导数最高占了18分,计数原理与概率统计最高占了15分。
其次,三角函数与解三角形、平面向量在每年试题中所占的分值基本稳定,分别为6 分和3 分。而对于算法与框图、圆锥曲线、微积分和极限这几个考点来说它们每年所占的分值起伏不大,基本上也就相差一个选择题或一个填空题。
4 高频考点剖析
下面对函数与导数、圆锥曲线、立体几何等几个考点进行进一步的分析。
4.1 函数与导数函数是学习数学知识的一大主线,导数往往是用来钻研函数性质的重要工具,从表3 考点分值分布中能够看出,函数与导数在每年特岗考试中都占有举足轻重的地位,考查时不光内容丰富,形式多样,而且在其他的内容上也会渗透进去考查。历年考试中函数与导数具体的考查情况见表4。
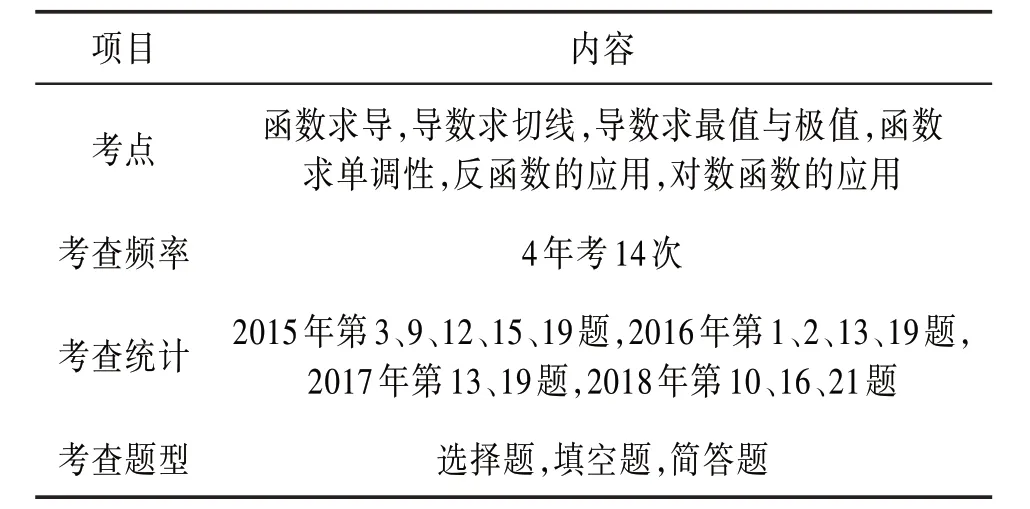
表4 试题中函数与导数考查情况
由表4的数据可以看出函数与导数是历年特岗教师考试的重中之重,一方面,它在近几年真题中考查频率达到了4 年考14 次的频率。对于这一模块来说考查的知识范围较广,比如基本初等函数的性质与应用、导数的性质与应用,包括函数求导、导数求切线、导数求单调性及导数求最值与极值等几个方面。
另一方面,可以看出考查的题型多样,每种题型都会有所涉及。值得留意的是在近几年的真题中,每年都有把函数与导数作为简答题的压轴题来考查,可见函数与导数所承载的选拔性功能尤为凸显,考试区分度更加的明显。现引用2018年特岗考试中函数与导数的题进行分析。


试题评析:首先,从这个题中可以明显地看出题目采用了两问的方式,从易到难,区分度较为明显。且它是一道综合性较强的试题,将函数求导、导数求单调性、极值、最值等几个方面紧密地联系在一起。
其次,第一问它所考查的是求函数的极值,这是一个常规的解法,只要求出函数的导数和函数的单调性,根据函数的单调性求出极值即可。而第二问考查的是含参求最值,做这个问时需要用到二次求导,这也很好地考查了考生的数学思维能力和计算能力,为选拔优秀人才提供了载体。
4.2 圆锥曲线圆锥曲线是解析几何中的核心内容,同时也是特岗考试中的重点考查对象,主要的内容有曲线与方程(圆、椭圆、双曲线、抛物线的方程)、圆锥曲线与直线的位置关系和圆锥曲线的综合应用。具体的考查情况见表5。

表5 试题中圆锥曲线考查情况
从表5 中可以看出,除2018 年外考查的题型都为一个选择题和一个简答题。其中选择题所考查的都是圆锥曲线的性质,简答题考查的是圆锥曲线的应用,难度较大,所以考生对圆锥曲线的理解不能只停留在表面,要看到知识的本质,不然在做简答题时,就会没有思路,找不到突破口。比如说下面两题:
例2 (2015 年第5 题〔3〕)已知双曲线的中心在原点,焦点在y轴上,一条渐近线的方程为x-2y=0,则它的离心率为( )。

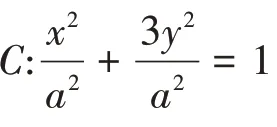
试题评析:从例2中可以看出,它所考查的是双曲线性质中的渐近线方程和离心率。这个题比较基础,只要了解双曲线的性质且会灵活地运用即可。
从例3 中可以看出,它所要考查的是椭圆上动点到定点距离的最大值,我们知道几何中的最值问题通常都是可以转化为函数问题来求解,因此本题中的动点到定点间的距离问题就可以构造出关于y的一个函数,通过求这个函数的值域就可以得到它的最值,这种利用函数法求最值的方法也是较为普遍的一种方法。
4.3 立体几何立体几何是特岗考试的热门考点,它主要考查考生的空间想象能力和逻辑思维能力。通过对近几年的真题统计分析不难看出,立体几何在每年的特岗考试中都会出现。具体的考查情况见表6。

表6 试题中立体几何考查情况
由表6可以看出立体几何在试卷中主要以简答题形式出现,其次是以填空题的形式来考查。从考点上来看,它所考查的知识点与高考试题中考查的知识点基本上是一致的,比如说下面的这两个真题:
例4 (2018 年第20 题〔4〕)如图1,所示的五面体ABCDEF 中,四边形ABCD 为梯形,且∠DAB=60°,EA=ED=AB=2EF=2,EF∕∕AB,M 为BC的中点。求证:FM∕∕BDE。

图1 题图
例5 (2017 年第21 题〔5〕)如图2,在直三棱柱ABC-A1B1C1中AB=1,AC=AA1=,∠ABC=60°。
(1)求证:AB ⊥A1C1;(2)求二面角A-A1C-B 的大小。

图2 题图
试题评析:立体几何证明主要是解决两类问题:一是证明平行垂直类问题,其中主要是证明线与线平行垂直、线与面平行垂直和面与面平行垂直,然而解决这一类问题通常采用它们的判定定理来求解。如例4 与例5 第一问;二是求解夹角问题,主要是求解异面直线所成的角、直线与平面所成的角和二面角,解决这类的问题主要是采用综合法和向量法来求解。综合法主要是考验考生的空间想象能力和逻辑思维能力,使用综合法来求解的关键是找到它们所成的角即可。向量法主要是考查考生数形结合的思想,将几何问题转化为代数问题,而使用向量法来求解的关键是建立空间直角坐标系、找出点的坐标和掌握向量的基本运算。无论是采用综合法还是向量法来求解,都是将角的问题转化为线线角来求解,考生可以根据自己的特长选择适当的方法来求解。
5 试题特点分析
5.1 层次分明根据近几年试题的考点来看,数学学科知识是特岗教师考试的重要考查点,主要考查考生在数学领域的基础知识。把数学学科基础知识分为初中、高中、大学3 个阶段,分析各阶段分值分布,见表7。

表7 各阶段分值分布表
从表7 中不难看出高中数学知识在数学学科基础知识中占主导地位,高达79.38%,初中、大学两部分的知识所占比例都相对较少也比较均衡,其中初中知识部分占比为9.37%,大学知识部分占比为11.25%。因此在备考时,可将着眼点放在高中的知识上。
5.2 综合性强从近几年的真题上来看,由于每份试题的容量有所限制,每一个知识点不可能都设计一个题来考查,所以真题基本上呈现的都是综合性的试题,将多个知识点紧密地联系在一起,主要来考查考生的综合分析能力、理解能力及逻辑思维能力等,比如说上面提到的例1,它考查导数时将多个导数的性质融汇在一起。不光考查了考生对基础知识的掌握能力,更主要的是考查考生的综合分析应用能力和灵活性,若平时习惯于死记硬背或是机械地进行模仿,不能灵活地应用,要正确且迅速地解决综合性强的题,是很困难的一件事。
5.3 基础性实在历年的特岗试题中有100 分的数学知识与20 分的教育知识,其数学知识占比有83.33%,数学基础知识占比66.67%。因此在备考过程中夯实数学基础是保证高分的关键,在掌握基础知识的过程中要注意数学基础知识和基本技能是形成和发展数学能力素养的必要基础,是领悟数学基本思想的重要载体,特岗考试对基础知识的考查不是对知识的机械记忆和简单模仿,而是侧重于考查考生对基本概念的理解及基本思想方法的应用〔5〕,其基础性实的属性也决定了备考过程中加快基础框架的构建是十分必要的。
5.4 理论联系实际纵观近几年的特岗真题,在某些题目的设计上重视联系生活实际,注意创设情境,在解决情境问题时,注重考查考生的信息处理能力〔6-7〕。如例6、7。
例6 (2017年第16题〔5〕)某公司一个月生产产品1 890 件,其中特级品540 件,一级品1 350 件,为了检验产品的包装质量,用分层抽样的方法,从产品中抽取一个容量为70的样本进行测试,其中抽取的特级品的件数是。
例7 (2018年第19题〔4〕)某校倡导为贫困生募捐,要求在自动购水机处买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱。现统计了连续5 d 的售出矿泉水箱数和所得捐款额情况,如表8:

表8 题表
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500 元;综合考核在21~50 名,获二等奖学金300元;综合考核在50名以后的,不得奖学金。
(1)若x 与y 成线性相关,则某天售出9 箱水时,预计所得捐款额为多少元?
(2)假设甲、乙、丙三名学生均获奖,且各自获一等奖和二等奖的可能性相同,求三人获得奖学金之和不超过1 000元的概率。
数学来源于生活,同时也必将应用于生活,学数学就是为了解决生活中所遇到的问题。以上两个题都是来自于日常生活中的案例,运用数学知识去分析和处理生活中的数据,进一步地考查了考生对知识点的理解和应用。
6 结论
本文通过收集整理2015—2018 年云南中学数学特岗教师考试真题,从试卷结构、考点内容、考点分值、高频考点和试题特点等几个方面进行了分析与研究,得到了如下结论:
首先,从中学数学特岗教师试卷的结构上来看,历年数学学科基础知识这一模块的试卷结构均由选择题、填空题、简答题三部分构成,共80 分,占试卷总分的2∕3,可见数学学科基础知识是拉开各考生的差距所在。因此在备考过程中累积数学学科基础知识是重要的。
其次,从试题的特点上来看,历年的数学学科基础知识中高中所占的比例都远远大于初中,高中的数学知识占比达79.38%,所以高中的数学知识更要牢牢把握,尤其是想在短时间内备考特岗教师的考生,重点复习高中数学知识,以此为基础开拓知识面,是快速备考特岗教师的关键。
最后,值得注意的就是,在各考点中函数与导数、圆锥曲线、立体几何、计数原理与概率统计这4类题型的总占比达到了35.83%,因此在备考过程中,这4类题型是值得研究和深入学习的,这样在考场上遇到这类高频率、高分值的题目,能够高效地作答也是为其他难题、新题争取更多突破的时间。

