压水堆堆芯Pin-by-pin计算扩散系数的计算方法研究

张斌 李云召 吴宏春 刘勇 王冬勇 王星博 钟旻霄

摘   要：压水堆堆芯中子学计算中，扩散系数对堆芯Pin-by-pin计算结果有着重要的影响。本文对扩散系数的计算方法进行了研究，基于菲克定律，研究了三种不同的扩散系数归并方法。基于KAIST基准题分析比较了不同少群扩散系数的求解方法对堆芯Pin-by-pin计算精度的影响，计算结果表明，采用以栅元总泄漏率守恒原则归并得到少群扩散系数的方法能兼顾特征值与棒功率的计算精度，拥有更好的计算效果。

关键词：Pin-by-pin计算  扩散系数  泄漏率守恒

中图分类号：O224                                  文献标识码：A                       文章编号：1674-098X（2020）05（a）-0069-03

受限于计算机的发展水平，全堆芯中子学非均匀一步法计算无法在实际压水堆燃料管理计算分析中得到应用。均匀化方法是目前使用的反应堆燃料管理计算的主要理论框架之一，其核心思想是对于在空间与能量尺度上总体跨度较大、精细分布较为复杂的介质，在局部范围内用“等效”的均匀介质近似代替一定的非均匀介质。均匀化方法的本质是在不影响宏观整体计算精度的前提下舍弃微观局部的特征，利用相应的“等效”均匀化参数进行堆芯低阶输运计算，以降低计算要求并提高计算速度。

在均匀化理论中，判断一个均匀化方法的好坏，除了由方法定义的均匀化参数应真实反映和保持均匀化区域的非均匀性之外，还应在随后堆芯计算中保证经由均匀化之后所求得的解与非均匀堆芯的计算结果相吻合[1]。在反应堆燃料管理计算中，均匀化前后要求反应堆有特征值、各能群反应率及各界面上的中子泄漏率这三个物理量保持守恒，即均匀化一般原理。

根据三大守恒量中栅元各个界面上的中子泄漏率守恒原则，可以得到扩散系数的严格定义如下：

（1）

式中：——扩散系数，单位cm;——中子流密度，单位（cm2·s）-1;——中子通量密度，单位（cm2·s）-1;hom——均匀化后的参数;het——均匀化前的参数。

由于中子泄漏率需要在栅元各个表面上都满足守恒条件可能会导致由此定义式定义的扩散系数在栅元各表面上彼此不相等，这与栅元内均匀化常数为系数的假设相互矛盾。均匀化栅元的扩散系数是常数将导致界面中子泄漏率的不守恒，且守恒条件无法通过调整扩散系数的值来达到，这导致高精度的堆芯中子学计算需要对扩散系数的计算方法进行研究。

1  扩散系数的计算方法研究

根据扩散理论中的菲克定律[2]可以得到被广泛使用的扩散系数的定义：

根据通量体积权重法可以得到栅格计算中Pin-by-pin均匀化少群扩散系数的归并方法有如下两种：

（1）对多群细区输运截面采用通量体积权重方法归并得到Pin-by-pin均匀化少群输运截面，然后根据公式（2）求得Pin-by-pin均匀化少群扩散系数，如公式（3）和公式（4）所示：

公式（10）保证了栅元总中子泄漏率守恒，可用于Pin-by-pin均匀化多群群扩散系数的能群归并计算，即方法3：对多群细区输运截面采用公式（5）归并得到Pin-by-pin均匀化多群输运截面，然后根据公式（6）求得Pin-by-pin均匀化多群扩散系数，再以公式（11）作为权重系数进行能群归并得到Pin-by-pin均匀化少群扩散系数，如公式（10）所示。

2  计算结果分析

本节的数值验证与分析主要基于KAIST基准题完成[4]。KAIST基准题于2000年由韩国先进科技学院（Korea Advanced Institute of Science and Technology， KAIST）核能與量子工程系核反应堆分析与粒子输运实验室发布。该基准题以堆内材料布置复杂、非均匀性强为特点。自发布至今已成为国际上Pin-by-pin均匀化数值验证工作中最具说服力的基准题之一。

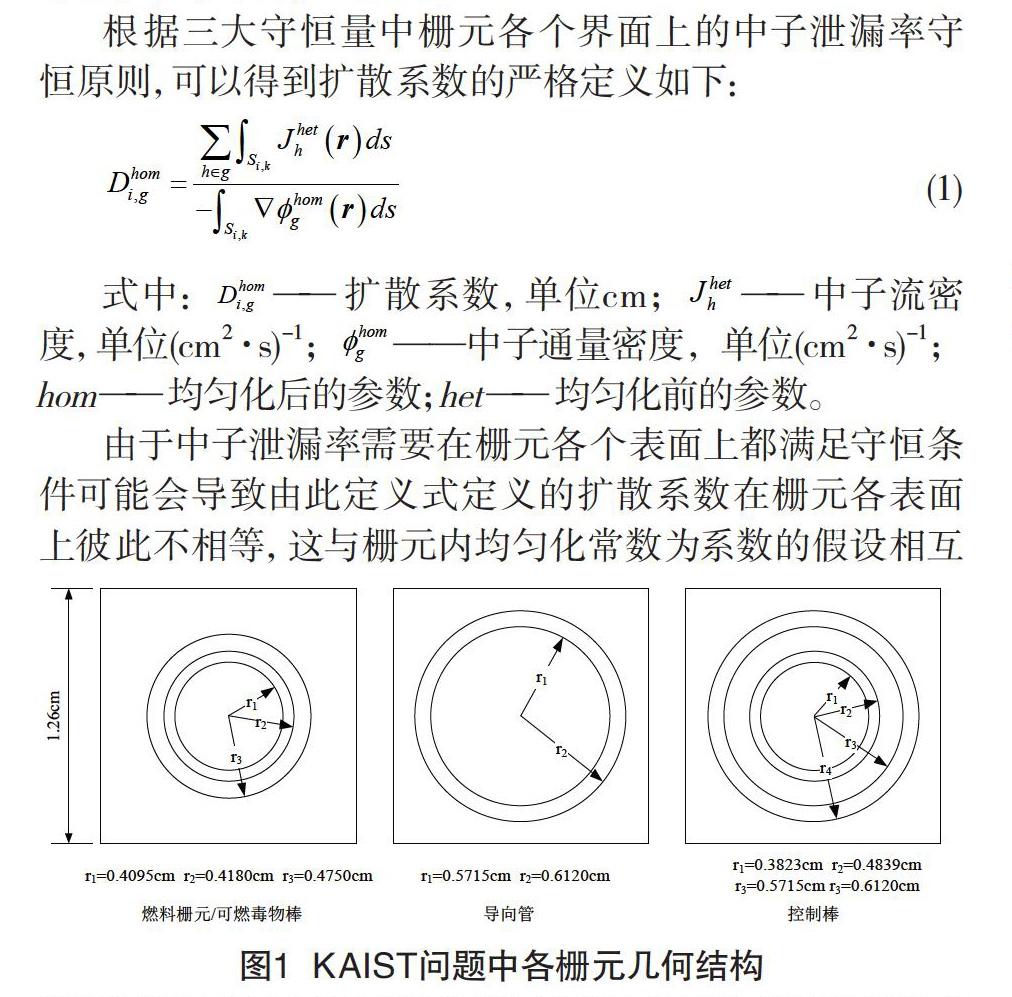
KAIST基准题包含三种组件，分别是富集度2.0%和3.3%的UO2组件和Pu浓度为4.3%、7.0%和8.7%分三区布置的MOX组件，分别命名为UOX-1，UOX-2，MOX组件。每种组件又有不带吸收棒、带控制棒（CR）和带可燃毒物棒（BA）三种情况。组件中出现的各栅元的几何结构如图1所示，UO2组件和MOX组件的几何布置如图 2所示。

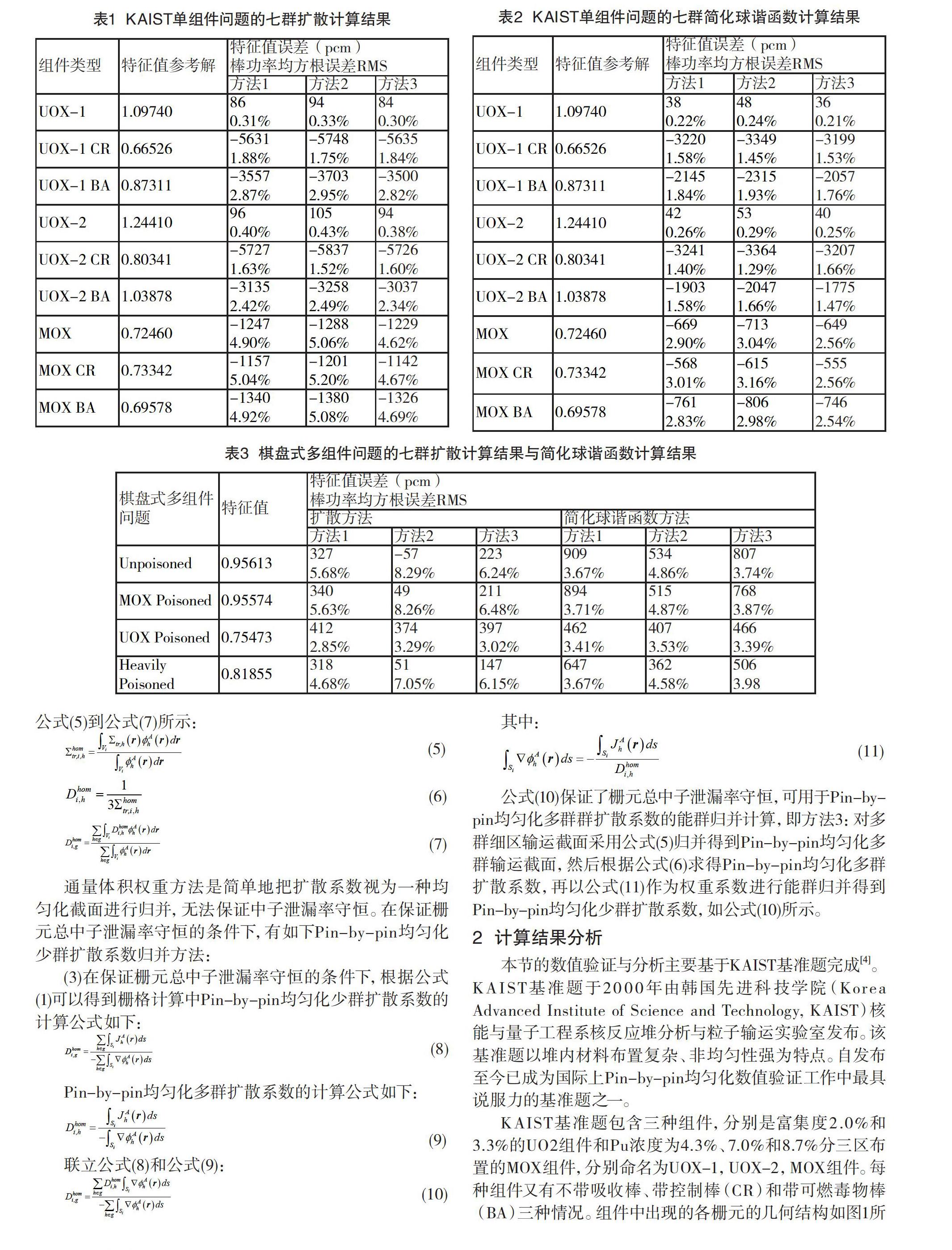
表1和表2给出了KAIST问题下单组件问题的两群扩散计算结果与简化球谐函数计算结果。表中结果从特征值误差和棒功率误差方面看，在单组件问题中，使用不同计算方法得到的少群扩散系数在堆芯Pin-by-pin计算中的计算精度相当，无论堆芯Pin-by-pin计算采用扩散方法还是简化球谐函数方法。造成这个结果的主要原因是由于单组件计算采用全反射边界条件，组件整体泄漏为零，因此不同的扩散系数求解方式对堆芯Pin-by-pin计算的影响较小。

为进一步比较分析不同少群均匀化扩散系数计算方法对堆芯Pin-by-pin计算精度的影响，针对多组件问题进行了计算。通过对上节中描述的UO2组件和MOX组件进行组合，KAIST基准题定义了四个不同的棋盘式多组件问题，如图3所示。这些棋盘式问题具有较强的非均匀性，且组件与组件之间的干涉效应较强。

对于KAIST基准题的棋盘式多组件问题，单组件栅格计算在进行Pin-by-pin均匀化时能群被压缩至七群。表 3给出了棋盘式多组件问题的七群扩散计算与简化球谐函数计算的结果。从结果中可以发现，以总截面直接求解得到少群均匀化扩散系数的方式，即方法1理论上不符合从多群高阶输运方程简化到少群低阶方程的过程，因此计算随着少群能群数的减少而误差增大;堆芯计算在使用从多群扩散系数利用栅元总泄漏率守恒原则归并得到的少群扩散系数即方法3时，能兼顾特征值误差与棒功率均方根误差，计算效果最好。

3  结语

本文针对压水堆堆芯Pin-by-pin计算扩散系数的计算方法进行了研究，结合其他等效均匀化少群常数，在单组件问题和棋盘式多组件问题上分析比较了不同少群扩散系数的求解方法对堆芯Pin-by-pin计算精度的影响。计算结果表明，全堆Pin-by-pin计算采用七群计算时，采用以栅元总泄漏率守恒原则归并得到少群扩散系数的方法能兼顾特征值与棒功率的计算精度，拥有更好的计算效果;

参考文献

[1] 谢仲生.压水堆核电厂堆芯燃料管理计算与优化[M].西安：西安交通大学出版社，2004.

[2] 谢仲生.核反应堆物理分析[M].北京：原子能出版社， 2008.

[3] Yu Lulin Lu Dong， Chao Yung-An. The calculation mehod for SP3 discontinuity factor and its application[J]. Annals of Nuclear Energy， 2014（69）：14-24.

[4] Cho NZ. Benchmark problems in reactor and particle transport physics， 2000. http：//nurapt.kaist.ac.kr.benchmark.