基于里卡蒂方法的H控制

王永超

(吉林师范大学 数学学院,吉林 长春 130000)

0 引言

H控制是近年来才发展起来的优化控制理论中的热门课题，以极大奇异值理论著称的H范数描述系统性能指标，产生的H控制在工程设计中起着越来越重要的作用，已取得了相当大的进展[1-6].本文基于里卡蒂方法，研究了奇异系统的状态反馈H次优控制问题，对其进行了补充.

1 预备知识

考虑具有如下形式的正则的奇异系统[7]

(1)

其中x(t)∈Rn是状态向量，u(t)∈Rm是控制输入，w(t)∈Rq是外部扰动，z(t)∈Rl是控制输出，E,A∈Rn×n，B∈Rn×m,C∈Rl×n，D∈Rl×m，E为奇异矩阵.

对奇异系统(1)做如下形式的状态反馈

u(t)=Kx(t),K∈Rm×n

(2)

得闭环系统为：

(3)

其中，Ac=A+B2K,Cc=C+DK.

对于奇异系统(1)及给定的正数γ>0，设计状态反馈控制器(2)，使闭环系统(3)是容许的，且从w到控制输出z的闭环传递函数Tzw(s)满足‖Tzw(s)‖<γ.

引理1[8]对于广义系统(E,A,B,C)和它的传递函数G(s)，下面的命题等价:

(i)(E,A)是容许的，且‖G(s)‖<γ.

(ii)存在可逆实矩阵X满足里卡蒂不等式

与之对应的H里卡蒂方程为：

(iii)存在可逆实矩阵X满足如下线性矩阵不等式

2 主要结果

下面给出基于里卡蒂方程的H控制器设计，对奇异系统(1)做如下假设:

(a)(E,A,B2)能稳且(E,A,C)能检测.

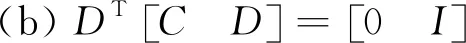
定理1对于满足假设(a)和(b)的奇异系统(1)，下面的命题等价.

(I)存在状态反馈矩阵K，使得闭环系统(3)是容许的，且‖Tzw(s)‖<γ.

(II)存在一个可逆矩阵X满足如下里卡蒂方程

(4)

如果命题(II)成立，则所求的一个容许的状态反馈矩阵为：

(5)

证明

Ⅰ⟹Ⅱ.设存在一个状态反馈K，使(E+B2K)是容许的‖Tzw(s)‖<γ.

根据引理1，存在一个可逆矩阵X满足如下里卡蒂方程：

(6)

整理得：

(7)

其中

(8)

从而矩阵X满足里卡蒂方程(4).

Ⅱ⟹Ⅰ.设可逆矩阵X满足里卡蒂方程：

且由式(5)知

则上式中

ZK=0，

从而有

成立，再根据引理1知闭环系统

是容许的,且‖Tzw(s)‖<γ.

3 结论

本文在奇异系统的基础上，基于里卡蒂方法讨论奇异系统的状态反馈H次优控制，通过设计状态反馈控制器，利用里卡蒂方法给出了问题的具体证明过程.