千吨级管廊吊装门式起重机主梁优化研究

郭宏亮 隋振华,2

1 上海振华重工(集团)股份有限公司2 中交公路长大桥建设国家工程研究中心有限公司

1 引言

传统管廊建设采用混凝土现浇模式，施工周期长。近些年，逐渐发展出先由工厂预制，再由现场起重机吊装的模式。这一模式极大地缩减了施工周期，并且可以避免天气对混凝土浇筑的影响，应用越来越广泛。2018年6月验收的成都市玉虹路地下综合管廊工程[1]，其单节管廊质量近60 t，是当时国内尺寸和质量都最大的预制管廊。该管廊在工厂制作过程中采用了门式起重机，而在现场安装时使用了大型履带式起重机。

在建的雄安新区综合管廊单节长度达到24 m，重达1 000 t，相较于近些年的施工案例，重量大幅上升。考虑到雄安施工场地的要求，用于作业的门式起重机自重必须尽可能小。而传统的设计通常结合规范和经验进行，如依据公式直接指定宽厚比，虽然大大简化了屈曲的设计流程，但因不考虑实际受力，往往导致比较高的安全余量。近些年发表的有关优化的文献中，大多是从强度和刚度角度考虑的，考虑屈曲的比较少。实际上，屈曲计算比较复杂，随着箱梁尺寸的增大，其对设计的影响也越大。

以振华重工正在研制的千吨级管廊吊装门式起重机为研究对象，首先用材料力学[2]方法，从理论上研究重量对结构的影响，得出量化的结果，然后综合考虑强度、刚度和屈曲这些复杂的约束条件，用遗传算法进行优化，探寻获得最优结构的方式方法，使其能以最小的重量，获得最大的起重能力。

2 起重机受力分析

该起重机大车轨距65 m，悬臂15 m，起吊重量1 000 t。起重机为双箱梁结构，以其中一条箱梁为研究对象，其受力主要来自两个方面，一是大梁自重，为均布载荷q；二是小车载荷与起吊重量形成的集中力P(见图1)。

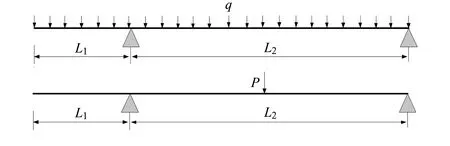
图1 大梁受力分析

初步方案估计单边大梁自重G=395 t，故均布载荷q=G/(L1+L2)=4.49 t/m。根据设计要求，确定作业系数为1.05，冲击系数1.1，横向偏心载荷系数10%，小车及吊钩吊绳总重324 t，经计算，单边集中力P=822 t。

根据上述参数，自重和集中力形成的大梁弯矩分布见图2。由图中可以看出，大梁自重引起的弯矩占总弯矩的比例约为10%。

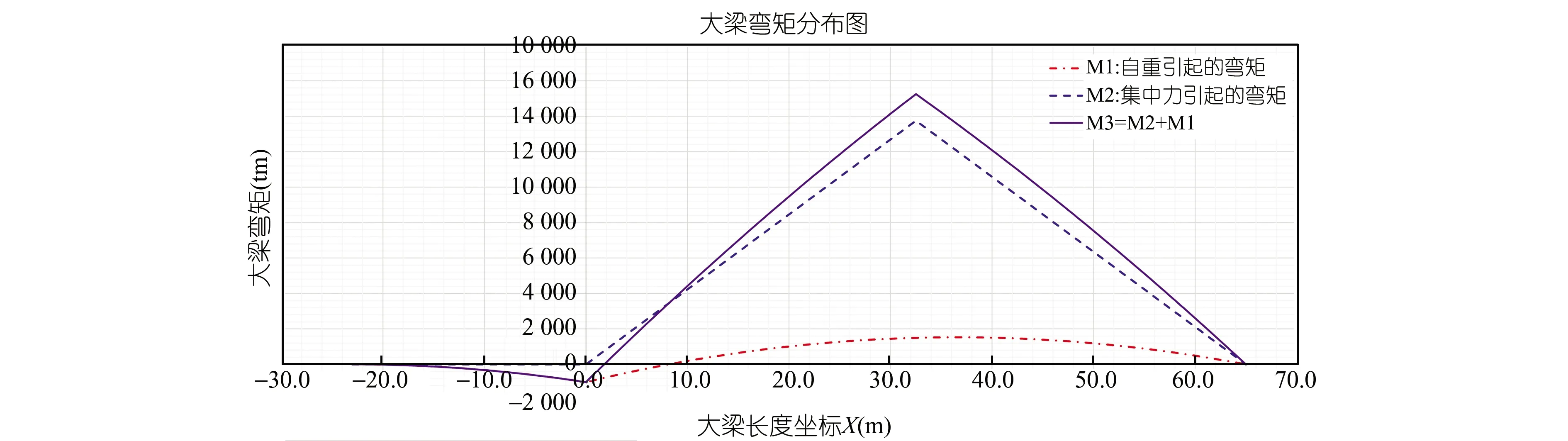
图2 大梁弯矩分析

结构优化主要从两个方面考虑：

(1)板厚。板厚增加，结构抗弯能力增加，但也会导致大梁重量的增加。如前所述，大梁自重引起的截面弯矩是不可忽略的，板厚增加在线性提高截面能力的同时，也增加了负载。

(2)梁高。由于翼板是梁截面抗弯惯性矩的主要构成方面，增加梁高将显著提高截面的抗弯惯性矩和截面模量。但是增加梁高的同时，腹板区格的宽度会加大，导致腹板区格的宽厚比增加，抗屈曲能力下降。这时又必须增加纵向筋，减小区格宽度。因此，单纯增加梁高，或者试图通过减少腹板厚度并增加翼板厚度来提高截面抗弯能力的方法，并不一定能满足所有的结构要求。

3 遗传算法

起重机大梁的优化是一个复杂的过程，几种要素引起的结果可能是相反的，复杂的屈曲问题也难以用简单的函数描述。考虑到种种复杂性，将采用遗传算法来实现优化目的。

遗传算法[3]通过模拟生物自然选择和遗传机制，实现优秀个体的搜索。通过编码技术，以数字串模拟染色体，以特定算法模拟染色体群体的进化过程。通过选择、交叉和变异等操作，获取适应性较好的串，从而生成新的串的群体，逐代进化继而获得最优解。遗传算法可以利用多种语言编写，如C#、Matlab等，本文将利用Python来编写遗传算法程序。

3.1 设计变量的选取

设计变量选取为：宽度A2,上翼板厚度D1,下翼板厚度K1，腹板高度H8，腹板厚度E1(见图3)。各变量的范围为：2 800 mm≤A2≤3 500 mm，5 000 mm≤H8≤8 000 mm，16 mm≤D2≤30 mm，16 mm≤K1≤30 mm，10 mm≤E1≤20 mm，筋板根据需要动态考虑。

图3 截面变量

3.2 优化目标函数的建立

优化目标为主梁结构重量最小。主梁结构重量为：

wt=Area×Length×dens×Cw

(1)

式中，Area为截面的含筋面积，mm2；Length为主梁长度，Length=(L1+L2)=88 000 mm；dens为密度，取7.85×10-6kg/mm3；Cw为考虑大梁上附加的轨道、隔板等的重量系数，根据具体项目，此处取Cw=1.22。

3.3 优化约束条件

根据《欧洲起重机械设计规范》[4]和中国起重机设计规范GB3811[4]，大梁的结构设计要求如下。

3.3.1 强度

计算应力应小于屈服极限除以安全系数，故约束条件IR1为：

(2)

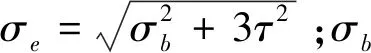
3.3.2 刚度

起重机的静刚度[6]是指小车起吊时，主梁在铅垂平面内的最大静挠度。该静挠度需要控制在一定的水平，以确保小车轨道变形不影响小车运行。计算静挠度时的计算载荷包括小车自重和起升载荷，但不包括起升冲击系数、工作系数及主梁自重。约束条件IR2为：

(3)

式中，δ为跨中计算变形；δa为许用变形，根据规范，δa=L2/750=86.67 mm。

3.3.3 屈曲

屈曲是指比较薄的钢板在局部受压时由平面状态变成屈曲状态，从而迅速丧失承载能力的现象。当板的边缘应力达到临界屈曲应力时，板就会发生屈曲(见图4)。

图4 平板屈曲

依据理论，临界屈曲应力与欧拉应力呈倍数关系，欧拉应力由下式给出：

(4)

式中，E为弹性模量；μ为泊松比；t为厚度；b为板材在垂直于压力方向的宽度尺寸，亦即大梁截面中由筋板分成的各个区格的宽度。临界屈曲应力计算如下：

(5)

式中，kσ被称为屈曲系数，其取决于板两边尺寸的比值α=a/b、板边的支撑情况、板在其本身平面内所受载荷的类型、板所用加强筋加强的情况。在大梁截面中，对4个自由边，因其边界条件为3边简支1边自由，故取kσ=0.42；而其他由纵筋分段的区格，因其4边均是简支状态，将根据边缘应力的比值ψ=σ2/σ1具体计算。

因此，临界屈曲应力不仅与几何有关，也与具体的应力状况有关，各个分段的临界屈曲应力是不同的。对一个截面而言，计算其屈曲是否满足要求，需逐个计算截面上各个纵筋处的应力，逐段计算屈曲相关值IR3i，所有区段的屈曲相关值向比较的最大值为该处的屈曲相关值：

(6)

屈曲设计约束可以由下式表示：

IR3=max(IR3,i)≤1.0

(7)

计算屈曲的过程非常复杂，可以借助Python编写的函数来实现。程序需要在梁高增加时动态调整筋板的数量。这些筋板是连续的，不仅提高了截面的抗弯能力，也因减小了板的局部宽厚比而提高了临界屈曲应力。

综上，起重机大梁优化的约束条件为：

IR=max(IR1,IR2,IR)≤1.0

(8)

3.4 罚函数的建立

由于遗传算法不能直接处理有约束的优化问题，本文利用罚函数方法将有约束问题转换为无约束问题。结合罚函数，修正目标函数如下：

wt=wt+(IR-0.95)2×1 800

(9)

式中，wt是大梁的质量。该目标函数的特点是，当IR远离0.95时，目标函数都将被放大，远离越多，质量放大越多，这样越劣质的解离可行域就越远，越优质的解离可行域就越近，由此引导遗传算法向最优个体群进化。

3.5 优化结果

与传统优化算法不同，遗传算法不依赖初始条件，因此其计算的第一代群体是随机生成的。经过大约60代后，群体表现出的强度、刚度和屈曲就已经趋于稳定。质量稳定在330 t左右(见图5)，但各相关值均小于1.0(见图6)，结构轻质高效，表现出了良好的力学性能。

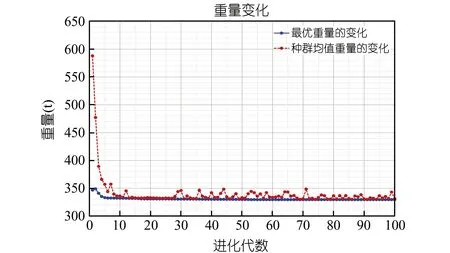
图5 历代解的进化追踪

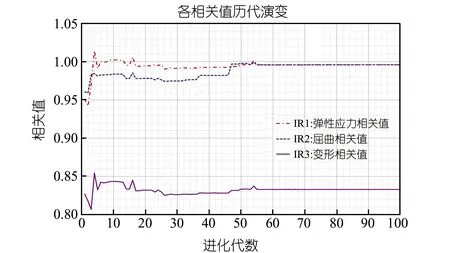
图6 进化过程中约束情况的变化

与原始方案的395 t相比，质量减少了65 t，下降了16.5%，详细优化参数见表1。

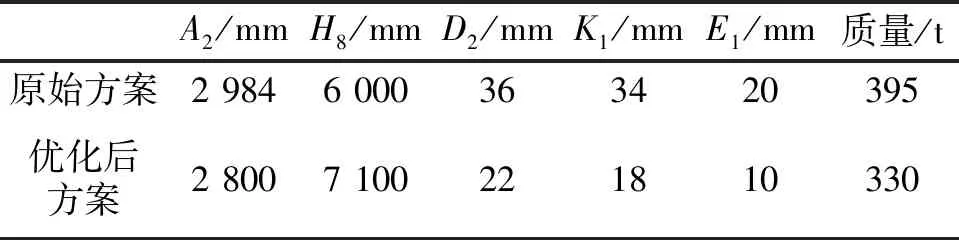
表1 优化结果总结

4 结语

随着起重机大型化发展，自重对结构的影响越来越大，薄壁箱梁的屈曲问题需要得到更多的重视。

通过对主梁优化建立目标函数，确定含屈曲的约束条件，用Python编写遗传算法程序进行优化，获得了较好的结果。主梁结构质量减少了16.5%，结构强度、刚度、局部屈曲均满足规范的要求。该方法解决了大型起重机优化中常常忽视却有重要意义的屈曲问题，可以推广应用到其他大尺寸薄壁截面机械的优化中。