基于岩石“等效损伤”探究宏观断裂规律

张向东，王 浩，敬鹏飞

(辽宁工程技术大学土木工程学院，辽宁 阜新 123000)

0 引言

岩石是一种天然的非均质材料，内部随机分布着众多形状各异的矿物颗粒、孔隙和微裂纹。有研究认为这些细观的孔隙和裂纹控制着岩石的损伤演化过程和变形路径，在一定程度上决定了岩石宏观力学特性和破裂特征。因此从细观尺度研究岩石孔隙和微裂纹如何影响岩石宏观变形破坏机理具有十分重要的意义。

随着计算机微电子技术的发展，电子显微镜技术(SEM)在细观岩石力学领域得到应用与发展。Sprunt和Brace最早将电镜扫描技术引入细观岩石破裂的研究中。Brace和Tapponnie研究了在应力诱发条件下的裂纹扩展，研究认为微裂纹不是由剪切力造成的，扩展的裂纹大多与颗粒边界有关。宫伟力等[1]用电镜扫描的手段研究深部条件下岩体损伤及煤与瓦斯突出机制及复杂孔隙结构对岩体非线性力学行为的影响。徐晓鹏等[2]运用扫描电镜拍摄了不同应力条件下水泥砂浆的实时细观结构图像,应用分形理论估算了细观结构图像的分形维数,分析了脆性材料的细观结构演化特征。周尚志等[3]基于SEM试验研究K2SiO3加固土的微结构量化分析及加固效果。马闫[4]通过可视化的SEM图像研究黄土的微观结构包含骨架颗粒、孔隙和骨架颗粒间的连结三部分,及由三要素组成的各种尺度的孔隙。张英等[5]运用扫描电子显微镜(SEM)试验和压汞(MIP)试验,通过数字图像处理技术对土样的微结构图像进行定量分析来揭示冻融循环对土体强度影响的微观机制。钱庆波等[6]通过单轴压缩试验，使用图像处理技术分析了单轴压缩条件下岩石中新生裂隙的萌生扩展过程。张向东等[7]采用三轴压缩试验，得出不同围压、不同加载速率下粉砂质泥岩的应力应变曲线，并与粉砂质泥岩的加载损伤模型相结合得到了粉砂质泥岩在加载过程中的损伤规律。施爱勇等[8]使用扫描电子显微镜(SEM)试验和Canny边缘检测技术得到并分析了偏心率，圆形度等土颗粒形状特征参数及各参数相关性、因子分析。数字图像识别技术及其处理方法为研究岩土工程材料的细观结构提供了一种新途径，利用数字图像处理技术处理图像可以非常准确的显示出岩石的细观结构。陈世江等[9]借助数字图像处理技术研究岩石节理，并开发了节理轮廓线分形维数计算程序,为分数维较准确方便地应用于工程实践做了有益的探索。况杰等[10]提出了一种基于相位一致性检测和分段线迭代连接并去除伪边缘的岩体裂隙自动检测方法。付茹等[11]借助于高精度的CT扫描技术和图像处理技术，获得近海石英砂和风化花岗岩残积砂这两类砂土颗粒的三维形态信息,采用球谐函数序列实现两种砂颗粒三维形态的准确重构。杨苏[12]基于数字照相量测系统所采集的裂隙图像,研究岩体裂隙识别与表征关键算法,并采用Delphi软件初步开发岩体裂隙识别与参数表征程序系统。陈从新等[13]应用数字图像处理进行的岩石细观力学研究及其对宏观力学响应和破坏机制的影响。尹小涛等[14]基于图像处理技术和CT试验对岩石裂纹量进行了量化描述。

分形几何是一门可以用来描述自然界不规则以及杂乱无章现象的数学分支，是一种在无序中寻找有序规律的新方法，其已成为岩石力学研究中解决复杂问题和工程实际问题非常有用的工具和方法[15]。李志清等[16]利用分形理论表征孔隙结构的非均质性,揭示分形维数和孔隙结构之间的关系。蒋赏等[17]依据分形理论计算钢筋混凝土表面裂缝分布的分形维数,并讨论分形维数与梁的荷载、跨中挠度、屈服荷载和冻融循环次数之间的关系。王金安等[18]应用激光技术和分形理论测量和描述岩石断裂表面粗糙度。陶高梁[19]采用分形理论对岩土介质孔隙结构展开研究，建立了土壤黏粒含量与其颗粒质量-粒径分布分维数的关系。赵洪宝等[20]基于分形理论展开了冲击载荷对煤样表面裂纹扩展特征影响研究。徐永福等[21]运用分形理论研究非饱和土力学性质，构建非饱和土孔隙分布的分形模型，并导出了非饱和土的水分特征曲线、渗透系数、剪切强度的表达式。孙秀丽等[22]基于分形理论对疏浚淤泥固化土孔隙结构进行了定量化研究。马新仿等[23]应用分形几何的原理,研究了低渗透储层岩石的孔隙结构,建立了毛细管压力和孔隙大小概率密度分布的分形几何模型。

岩石属于脆性材料，在宏观裂纹出现之前，已产生了微观裂纹与微观空洞，人们将这些微观缺陷的出现和扩展称为损伤[24]。岩石的最终宏观断裂破坏与其内部微裂纹的发育聚集有着密切联系，本文主要集中研究细观尺度下蠕变损伤、加载损伤和冻融损伤裂纹演化规律，借助电子显微技术及数字图像处理技术对损伤裂纹一一做出几何特征描述。研究分析认为岩石损伤具有等效性，这种等效是唯像的等效。基于唯像理论理念，直接分析多因素耦合损伤裂纹，采用分形理论和统计学理论，对岩石力学特性做出细观损伤描述、裂纹尖端运动描述和宏观断裂描述，得出细观损伤对宏观断裂影响的数学规律。

1 损伤裂隙观测试验

1.1 试验试件制备及仪器选择

损伤试件选用同一煤矿相同砂岩，制备试件尺寸为蠕变损伤试件采用GDS试验机进行蠕变试验，轴压选择试件抗压强度的60%～80%，可获得较好的蠕变三阶段曲线，分别取蠕变加载7 d、14 d、21 d和28 d的试件做SEM扫描试验。加载损伤试件：采用普通三轴加载机进行加载试验，加载破坏后对试件进行SEM扫描试验；冻融循环损伤试件：采用YH-40B型标准恒温恒湿养护箱进行冻融循环试验，分别取冻融3次、6次、9次和12次的试件进行SEM扫描试验。

观测试验采用QUANTA-250型扫描电子显微镜(SEM)，SEM通过发射并接收一束极细的电子束对试样表面进行扫描，最大可放大30 000倍，图象处理器高达4 096×3 536像素，满足观测要求。

1.2 试验方案

首先对无加载损伤试件进行电镜扫描。然后选取刚经历岩石蠕变损伤、加载损伤与冻融循环损伤的试件进行损伤裂纹边缘特征观测，SEM试验选择裂纹发育的部位进行观测。再利用MATLAB对观测的部位的SEM图片进行降噪和二值化处理。最后利用IPP数字图像处理软件对已进行降噪和二值化处理的SEM图片中的微裂隙进行几何要素(Area,Size (length),Size (width),Roundness,Fractal Dimension)测量及对比。

2 SEM图片处理分析

2.1 降噪及二值化处理

利用MATLAB对SEM图片进行二值化处理。二值化就是岩石晶体颗粒和裂纹以灰度图像显示出来，二值化对于孔隙边缘特征的提取至关重要，将二值化的阈值(灰度值)分别设置为75、80和85，不同的二值化阈值处理后的效果如图1所示。

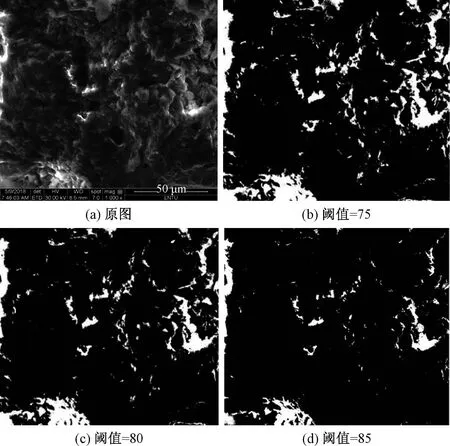
图1 不同阈值的二值化图像处理Fig.1 Binary image processing under different thresholds

通过图1可以看出，降噪及二值化的图像空隙边缘更加清晰，更能反映出损伤裂纹演化的复杂规律。若二值化阈值设置的太低，颗粒骨架可能会被处理成孔隙进行计算；若阈值设置过高，空隙可能会被当做是岩石晶体，阈值为80时颗粒骨架和空隙可被明显的区分出来，更符合颗粒和空隙真实的空间结构分布规律，故论文统一选择80灰度值进行二值化处理。

2.2 IPP数字图像处理软件几何要素测量

裂纹边缘提取完成后，利用IPP图像处理技术对SEM处理后的观测裂纹进行几何要素测量分析。将剥离的孔隙边缘特征进行提取，将其作为IPP的“AOI”区域并进行编码，如图2所示。

图2 微裂纹“AOI”区域选取Fig.2 Selection of micro crack “AOI” region

然后利用“Measurement”功能对SEM处理过的图片的空隙边缘的几何特征进行测量，损伤显著部分测量数据见表1。

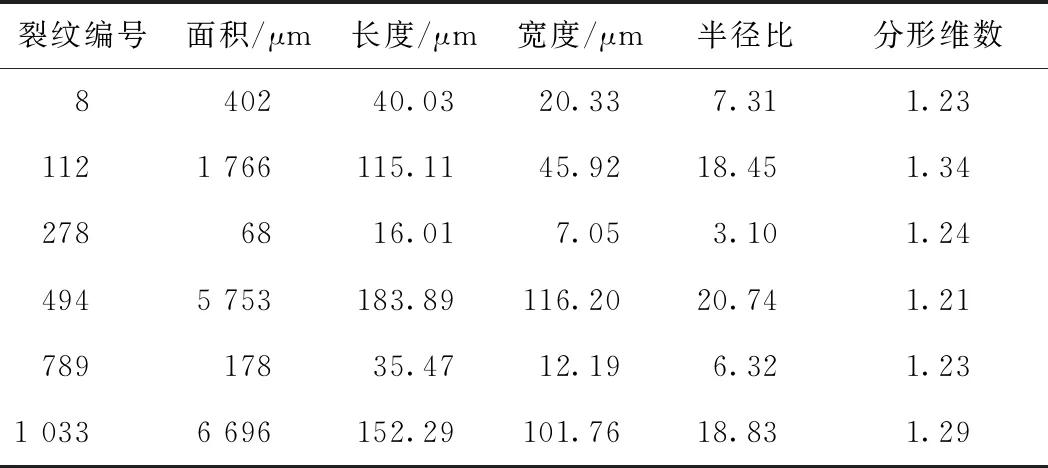
表1 部分“AIO”几何要素提取

由表1可以看出明显看出：损伤微裂纹数目众多、裂纹面积各不相同，每个裂纹大小也不规则，复杂无序难以用常规手段统计其内在规律，而每个裂纹都可以用分形维数来描述其边缘的复杂程度，而且所有裂纹也服从统计自相似分布。

2.3 不同损伤微裂纹对比分析

整个研究过程处理分析图片过多，因此文中只选用不同损伤的某个阶段裂纹明显且具有代表的试件与原始试件进行对比分析。冻融损伤选用冻融循环9次SEM图片；蠕变损伤试件选用经历蠕变加载21 d；加载损伤选择加载前与加载后的SEM图片；耦合损伤试件选用冻融9次、蠕变加载21 d的SEM图片。损伤前后拍摄位置稍有偏差，但主裂纹基本保留，如图3所示。

图3 试件损伤前后对比Fig.3 Comparison before and after specimen injured

通过SEM观测对比发现岩石缺陷存在损伤裂纹与原生孔隙，研究损伤裂纹需将其区分出来。原生孔隙与损伤裂纹几何特征有很大区别，前者更接近圆形或椭圆形，而后者更像无规则曲线。本文引入Roundness(圆度值)描述岩石缺陷。圆度即圆整程度可以用来描述不规则图形接近圆的程度。

(2.1)

式中L为研究对象外轮廓周长,(单位μm)由公式(2.1)可知标准圆圆度值为1，接近线状多边形其圆度值趋于无穷大，圆度值越大，周长转化为面积的转化率越低。故可以采用圆度值来区分原生孔隙与损伤裂纹。观察发现原生裂纹的圆度值都小于4，故本文将缺陷圆度角小于4，视作原生孔隙；圆度角大于4，视作损伤裂纹。

通过对冻融不同循环次数的损伤裂隙、蠕变不同时间阶段的损伤裂隙SEM图片做对比来分析，研究损伤裂纹的演化规律。冻融循环损伤裂纹几何要素见表2，蠕变损伤裂纹几何要素见表3。

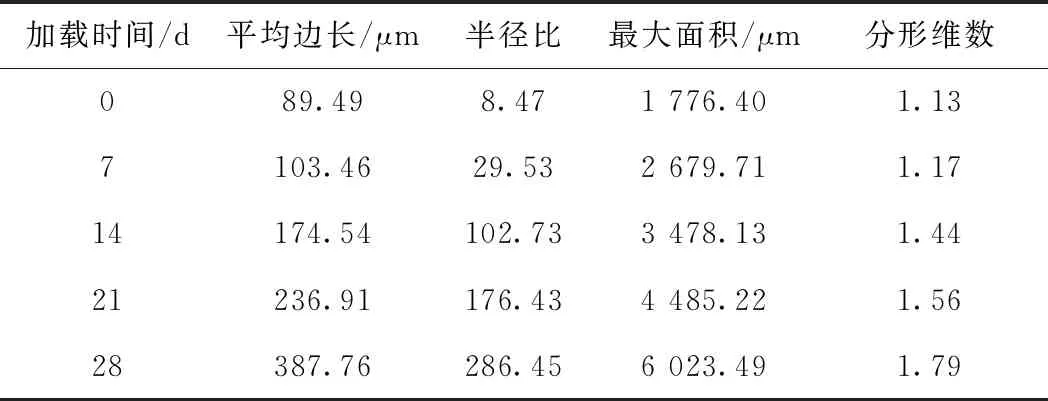
表3 蠕变损伤裂纹几何要素

由表2、表3以及表4可知，裂纹随着损伤程度的增加，平均边长、最大面积不断变大，冻融损伤裂纹平均边长可达到295.12 μm，最大裂纹面积可达到6 023.49 μm2。半径比增长速率呈现增大的趋势。图3中所有裂纹中，最长的长边尺寸和最大的裂纹面积均为同一编号“AOI”，这一裂隙增长最快，且在之后的损伤程中，这一裂隙一直均保持着此特点。说明最大的微裂纹在损伤过程中，扩展最快，面积增长最大，且一直保持这个特点，直至破坏，将这一现象称为最大缺陷重点发育现象。分析认为最大缺陷重点发育现象，主要是由应力集中造成的。图4给出了9次冻融和蠕变21 d时空隙长度和宽度与面积的线性相关性。

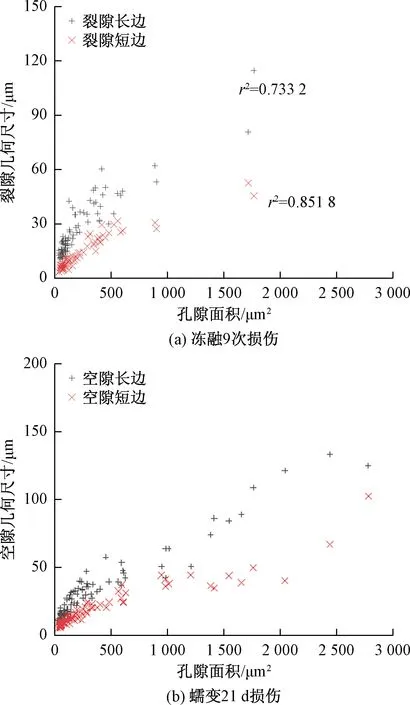
图4 裂纹长宽与面积的相关性Fig.4 Correlation between crack length and width and area

由图4可知，裂纹面积与孔隙的长度和宽度具有一定的相关性，裂纹的宽度和面积的相关系数为0.851 8；裂纹的长度和面积的相关系数为0.733 2；研究发现不同因素造成的损伤裂纹都具有这个特征，分析认为岩石裂纹宽度与面积的相关系数总是大于长度与面积的相关系数，主要是由岩石各向异性造成的，岩石裂纹长度扩展速率远大于宽度的宽展速率。随着裂纹扩展产生“短板效应”，短边成为了决定面积增长的限制因素，与面积增长相关性更强，同时印证了岩石在细观尺度下损伤微裂纹与宏观裂纹的各向异性是统一的。

利用IPP图像处理软件分析各种损伤的裂纹发现很多相同演化规律：

(1)随着损伤程度增加，微裂纹平均边长、面积不断变大；

(2)大缺陷重点发育，最大的微裂纹在损伤过程中，扩展最快，面积增长最大，且一直保持这个特点，直至破坏；

(3)任意一条微裂纹宽度扩展速率远小于其长度的扩展速率；

(4)扩展的微裂纹具有自相似特征，其分形维数随损伤程度增加而增加，当出现间断跳跃点可认为岩石损伤破坏。

本文通过对砂岩试件在三种损伤状态下细观裂纹的观察发现。无论是冻融损伤的试件、蠕变损伤的试件和加载损伤的试件都呈现以下规律：微裂纹宽度扩展速率远小于长度的扩展速率；最大微裂纹在损伤过程中，扩展最快，面积增长最大，且一直保持这个特点，直至破坏，认为这一现象为最大缺陷重点发育现象；研究发现不同因素造成的损伤裂纹的长度与面积相关性很高，相关性系数在0.8左右，分析认为岩石裂纹宽度与面积的相关系数总是大于长度与面积的相关系数，主要是由岩石各向异性造成的；岩石颗粒排布规律不同造成岩石微裂纹扩展的各向异性，岩石裂纹长度扩展速率远大于宽度的宽展速率。随着裂纹扩展产生“短板效应”，短边成为了决定面积增长的限制因素，与面积增长相关性更强，同时印证了岩石在细观尺度下损伤微裂纹与宏观断裂的各向异性是统一的；基于唯像理论，我们认为岩石由不同损伤因素造成相同的微裂纹，那么我们可以将不同因素造成的损伤视做等效，故可以将微裂纹发育过程中表现出大缺陷重点发育、裂纹扩展各项向性和生长微裂纹具有自相似性等特征的岩石损伤看做“等效损伤”。

3 “等效损伤”对宏观断裂影响研究

目前流行的断裂力学，包括线弹性断裂力学(Griffithrwin理论)和弹塑性断裂力学(HRR奇异性理论)可称为宏观断裂力学。它不计构件内部晶体间的变化及其引起的力学效应，只是从整体宏观裂纹产生的力学效应，从而导出裂纹扩展规律。但是岩石构造上的特点决定了我们不能完全从断裂力学理论出发去研究岩石断裂和破碎问题,必须建立宏观断裂理论与细观损伤机理的关系，将宏观断裂理论建立于微裂纹演化的微观或细观动力学基础上[15]。宏观断裂的现象是由岩石材料的细观损伤造成的裂纹逐渐扩展贯通造成的。然而，岩石材料的不均匀性、无序性和各种尺度缺陷随机分布与发展，使得这种现象只能通过统计的手段进行描述。分形几何是一门可以用来描述自然界不规则以及杂乱无章现象的数学分支，为研究不规则事物提供一种新方法。Weibull(1939)应用最弱环原理对材料强度做统计分析，该理论认为构成材料的微单元强度符合某种概率分布，当微单元的应力达到了强度值，构件就发生破裂。目前，统计理论和分形理论己经成为解决不定性问题的主要手段之一。

统计理论和分形理论在岩石力学的分析过程中可以进行三个阶段的描述：细观损伤描述、裂隙演化规律描述及宏观断裂描述。首先针对微损伤的状态进行细观描述，并得出状态变化的细观动力学。然后根据裂隙尖端运动，推导确定裂隙尖端运动方程，并以应力强度因子为“桥梁”，建立细观运动与宏观现象之间的关系。最后从统计分形分布函数出发进行宏观描述，做出相应的统计平均，得出微损伤对宏观力学性能的影响。

3.1 细观损伤规律

大量研究表明岩石从微观损伤发展到宏观断裂的过程是分形，其几何量和力学量都具有分形特性。裂纹的分布也具有统计自相似特征可用分形的基本关系—幂律关系很好的描述[25]。

N=Ca-D

(1)

式中：N—裂纹尺寸大于a微裂纹数目；

a——Griffith裂隙半长；

C——比例常数；

D——分形维数。

微裂纹尺寸的分布函数为式(2)，密度函数为式(3)。

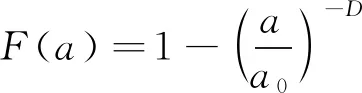
(2)

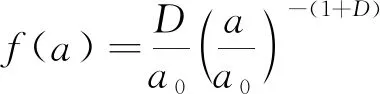
(3)

式中：a0——原始裂纹尺寸。

考虑两等同事件：P{σ≥σc}=P{a≥ac}，则一条微裂纹在应力σ下引发断裂的概率为：

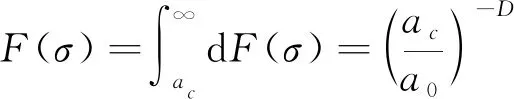
(4)

式中：ac——σ下裂裂纹失稳扩展的临界尺寸

由脆性断裂临界条件：

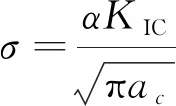
(5)

得到：

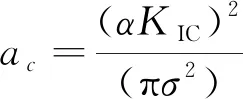
(6)

(7)

可得出试件在应力σ下的总断裂概率为：

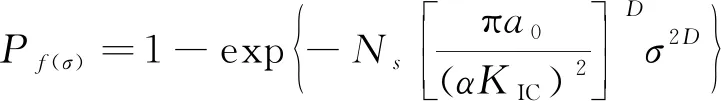
(8)

3.2 沿分形路径扩展的裂纹尖端运动规律

岩石在动、静荷载作用下裂纹扩展研究无论在理论上还是在工程应用上均具有重要意义，论文采用分形几何理论来描述动、静态裂纹扩展的不规则性，分析分形裂纹扩展对速度和应力强度因子的影响。应力强度因子K是反映裂纹尖端弹性应力场强弱的物理量，可以描述裂纹扩展能力。临界应力强度因子KIC又称断裂韧性，是试样或构件中有裂纹或类裂纹缺陷情形下发生以其为起点的不再随着载荷增加而快速断裂，即发生所谓不稳定断裂时，显示材料的阻抗值。分形裂纹扩展中分形裂纹速度、裂纹长度和裂纹弯折角对动态强度都有影响。谢和平根据分形插值理论提出应力强度因子[25]为：

K(L(D,t),V)=h(V)K(L(D,t),0)

(9)

式中：h(V)——瞬时分形裂纹速度的普适

K(L(D，t),V，0)——沿分形路径扩展的准静态(平衡)应力强度因子。

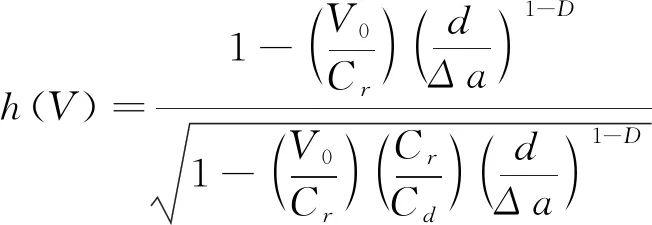
(10)

式中:V0——表观(实测)裂纹速度，

Cr——Rayleigh，

Δa——裂纹扩展步长，

Cd——弹性膨胀波速。

从公式我们可以看出h(V)取决于弹性波速和材料常数，而与加载条件无关。

K(L(D，t),V，0)中包含的两个静态效应，第一分形裂纹的弯折效应，第二分形裂纹不规则扩展的长度效应。因此可以把分形裂纹扩展的静态效应分解为：

(11)

式中：θ——分形裂纹的扩展弯矩角。

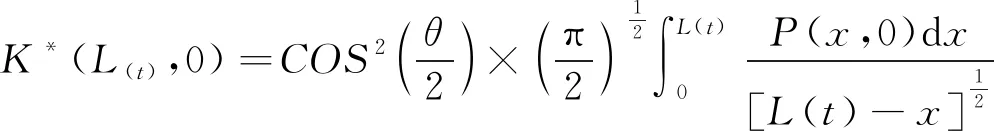
(12)

通过强度因子K(L(D，t),0)可以很好的描述裂纹尖端扩展运动，岩石裂纹由细观尺度扩展到宏观尺度的过程，是尖端裂纹扩展运动的结果，可将裂纹尖端扩展运动视作细观尺度到宏观尺度的源动力，也就是裂纹尖端扩展运动是跨尺度运动。

3.3 宏观断裂规律

断裂力学认为材料内应力达到应力峰值后发生断裂，根据损伤力学基于最弱环原理，我们将岩石试件抽象为一条N个环组成的链，SEM观测单元抽象为组成链的环。设每个环在应力σ时的断裂规律为F(σ)，假设最弱环的断裂导致整条链断裂，则在应力σ时整条链断裂的Pf概率，取岩石断裂强度σc为强度的数学期望，由概率论[25]：

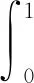
(17)

将式(8)代入上式可得：

(18)

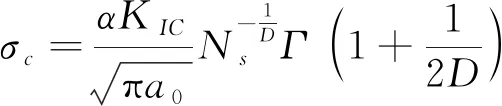
(19)

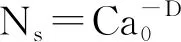
(20)

4 断裂强度公式结果正确性验证

通过室内“复杂耦合损伤岩石试件加载破坏”试验数据对式(20)进行验证。选择10个岩性较好的砂岩试件，采用GDS岩石蠕变仪进行为期6 d蠕变加载，GDS蠕变仪同时可以调控加载仓温度，分别设置加载仓温度-15 ℃和20 ℃，进行时间间隔1 d的循环冻融，最终得到经历了6 d蠕变加载和3次冻融循环的耦合损伤试件，然后进行SEM扫描，最后进行单轴加载破坏试验。选取两个明显特征的耦合损伤试件SEM图片处理如图5所示，数据见表4。

现以试件1为例进行计算，通过表4可知微裂纹数目N及分维D，根据式(1)得，C=9.41×10-6；根据式(10)得，h(V)=0.718，根据式(11)和式(12)得K(L(D,t)，0)=3.09K(L(D，t),V)=2.218 6，σc=21.08 MPa。

原始试件单轴加载断裂强度在32.6～47 MPa 范围内。耦合损伤试件断裂加载试验数据与理论值见表5。

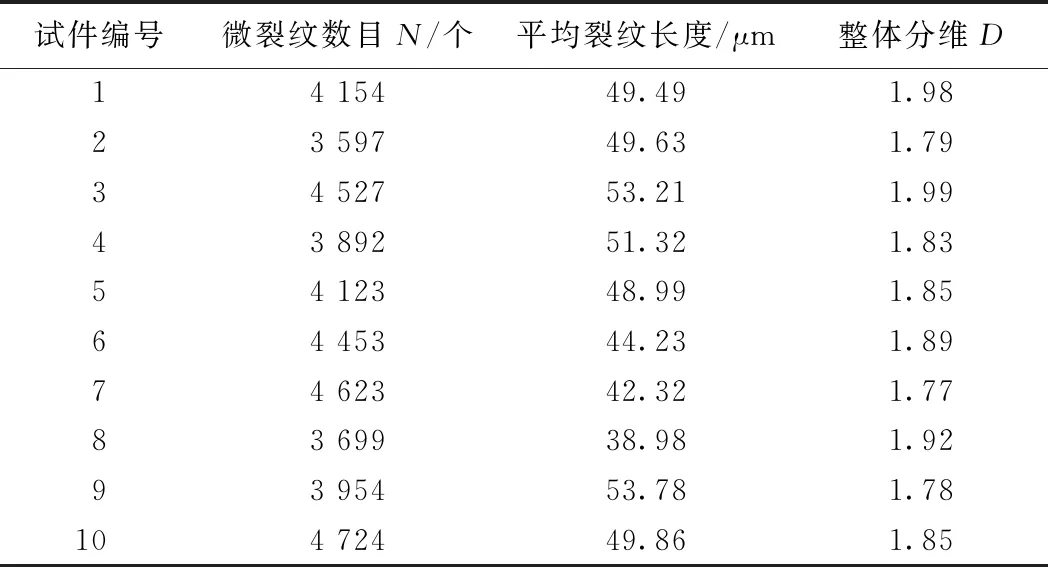
表4 耦合损伤统计数据

由表5可知，通过10组砂岩实测数据与理论数据对比分析，发现实际断裂强度与理论值存在误差，误差在5.5%范围内。误差分析，细观尺度上主要围绕大主裂纹进行统计，而忽略了小微裂隙的发育，研究发现非主裂纹也会影响其最终断裂强度；裂纹尖端扩展速率影响断裂韧性，而尖端扩展速率不好预测，只能取平均扩展速率进行计算。通过验证试验数据发现，利用等效损伤理论来计算复杂的耦合损伤问题，不仅简化了计算步骤，同时也能得到与实际相近的理论值。

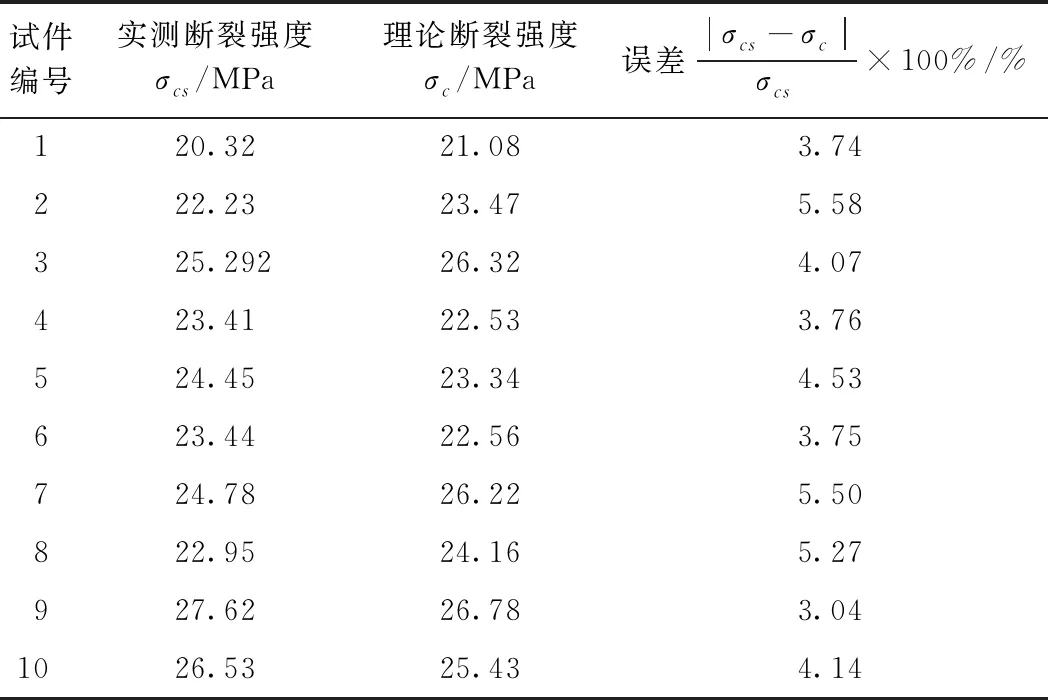
表5 试验值与理论计算值对比

5 结论

根据细观研究发现岩石不同损伤裂隙的发育具有相似的演化规律，继而展开了“岩石损伤裂隙等效性”研究，得到以下结论：

(1)岩石细观损伤与宏观力学特性相对统一。细观大缺陷重点发育现象，是宏观应力集中现象的细观体现；微裂纹宽度扩展速率远小于长度的扩展速率体现了岩石力学各向异性；

(2)基于唯像性理论认为岩石微裂纹发育过程中表现出大缺陷重点发育、微裂纹扩展各向异性和生长微裂纹具有自相似性等特征的岩石损伤可看做“等效损伤”；

(3)分形路径下的裂纹尖端扩展运动规律可以很好的描述损伤演化过程，通过微裂隙由细观扩展到宏观的运动规律可得到应力强度因子变化规律，应力强度因子可以定量表征裂隙扩展能力，可认为应力强度因子就是细观尺度到宏观尺度的“桥梁”；

(4)基于“等效损伤”建立细观损伤对宏观断裂影响的数学关系，通过室内试验数据验证等效损伤可以解决复杂的耦合损伤问题，且宏观尺度下“等效损伤”依旧成立。

本文为研究复杂的耦合损伤影响宏观力学特征问题提供一种简化思路，但是论文提出的“岩石等效损伤”假说仍需要大量研究验证。损伤等效还处于唯像的等效阶段，不同损伤对宏观力学特征影响的权重问题及确定“等效损伤因子”及本构方程建立问题有待进一步研究。