网络画板在圆锥曲线定点定值问题中的应用
文/中山市实验中学
新课标下的高中数学,越来越重视对学生综合素质的考察,圆锥曲线中的定点定值问题便是考查学生综合数学素质的一个重要途径.此类问题不仅涉及圆锥曲线的定义、直线与圆锥曲线的位置关系,还牵涉到函数,方程等代数方面的知识.它最大的特点是难以理解,难以想象,计算量大,这使得学生一遇到这类问题就望而止步.网络画板的应用使得本身很枯燥的课堂瞬间有了活力,让学生可以在直观上理解这类问题,提供了“探究-证明”的授课方式.先让学生产生兴趣,再授以解决这类问题的一般方法,相比传统的教学方法效果更好,也更能让学生接受.下面以几个典型例题为例来讲解.
一、定点问题


Δ=64m2k2-16(3+4k2)(m2-3)>0,即3+4k2-m2>0,
∵以AB为直径的圆过椭圆的右顶点M(2,0),且kAM·kBM=-1,


当m=-2k时,l:y=k(x-2),直线过定点(2,0),与已知矛盾;


总结:本题为“弦对定点张直角”的一个典型例题,可以推广到以下两种情形,再通过网络画板进行验证.
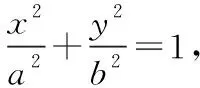

(2)“手电筒”模型:过圆锥曲线上任意一点M(x0,y0)作两条直线MA,MB,分别交圆锥曲线于A,B两点,只要给定一个限定MA与MB的条件(如kMA+kMB=定值,kMA·kMB=定值),直线AB依然会过定点(因为三条直线形似手电筒,固名曰手电筒模型).
探究:先构造三个变量n,a,b,用一个隐函数方程if(n=1,x2/a2+y2/b2-1,if(n=2,x2/a2-y2/b2-1,y2-2px))表示三类圆锥曲线,在其上取两个点M和A,连接MA,作直线MB,和圆锥曲线交于点B,在kMA+kMB和kMA·kMB为定值的条件下,我们通过运动点A发现直线AB恒过一个异于M的定点,变换n,k的值和M的位置,发现结论依然成立.
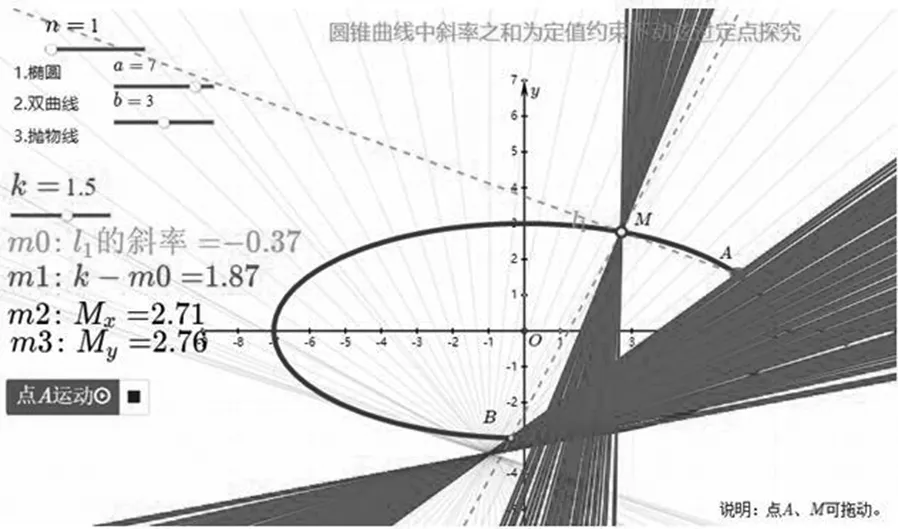

通过动态展示,学生在直观上更容易接受这个结论,可以鼓励学生按照例1的方法去证明,从而加深学生对这种题型的理解,掌握解题技巧.
二、定值问题
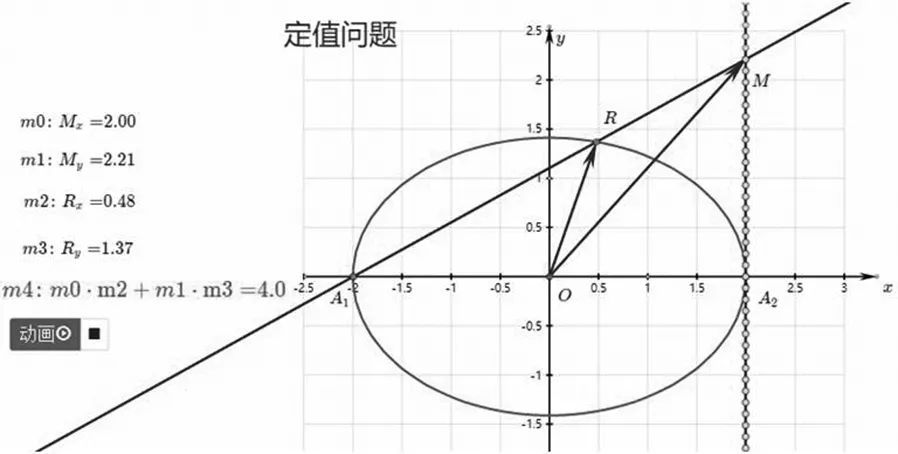

总结:本题中A1是一个固定的点,对于任意一点A,我们可以推广到以下一般情形:


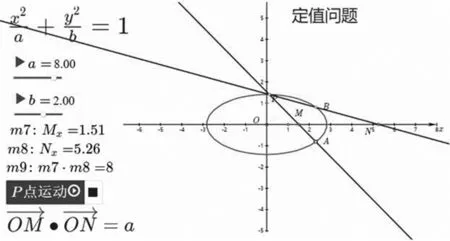

圆锥曲线定点定值问题博大精深,如果仅仅告知学生结论,学生很难在已有的认知水平内理解和接受,网络画板的辅助应用,可以对学生进行启发式教学,引导学生自己去探索,还可以实现课上到课下的延伸,激发学生的学习兴趣.

