水泵水轮机泵工况轴向力特性分析与改善
林文华 毛中宇 李向阳 徐步超 陶 然 王正伟
(1.国网新源控股有限公司福建仙游抽水蓄能有限公司, 仙游 351200;2.清华大学能源与动力工程系, 北京 100084)
0 引言
抽水蓄能电站是电网中重要的储能与调节单元,在电能富余时进行抽水,将电能转化为水的势能进行储存,在电能紧缺时进行发电、补充电网,在电网不稳定时进行调峰、调相,在发生事故时可黑启动等[1]。水泵水轮机是一种可逆式机组,其转轮双向旋转兼顾抽水与发电,结构紧凑、运行灵活,成为现代抽水蓄能电站的核心部件[2]。抽水蓄能水泵水轮机多为立式机组,为了防止抬机事故的发生,在机组尤其是转轮部件设计时,一般使其具有一定大小、方向向下的轴向力[3]。转轮所受的轴向力及其自重加载于推力轴承、并承载于上机架。然而,在泵工况运行时,转轮向下的轴向力容易出现过大现象,使承重结构发生变形并引起机组运行安全隐患。
水力机械轴向力的理论分析是工程中最为常用的方法[4]。文献[5]根据理论与经验公式,建立了水泵水轮机轴向力预测的数学模型,并分析了机组轴向力特性,结果表明,止漏环漏水量和高压腔内水流的旋转角速度是水泵水轮机轴向力特性的关键影响因素。文献[6]同样研究了水泵水轮机轴向力特性,认为转轮密封环以外的部分承压面大,对轴向力特性影响显著。随着计算机性能的不断提高、计算流体动力学(CFD)技术的不断完善,CFD成为当今研究机组流动特性[7-8]与轴向力特性的一种重要方法[9]。许多研究者在轴向力理论分析与间隙建模的基础上,进一步将CFD应用于水力机械轴向力的研究与分析。文献[10]通过CFD模拟发现,转轮内表面所受轴向力占水力机械轴向力的比例较大,是影响轴向力的最重要因素。文献[11]通过CFD模拟发现,转轮内表面轴向力受水力设计制约,而平衡叶轮前后盖板间隙间的压差则是调节水力机械轴向力的主要可行途径。
可以看出,平衡转轮上下腔体中的压力分布可以最大程度地抵消流体介质在转轮体上产生的轴向力特性。平衡盘与平衡孔是工程中最常见的两种平衡轴向力的方式。文献[12]采用平衡孔结构连接转轮两侧腔体,通过CFD分析发现,平衡孔结构减弱了离心泵的轴向力特征。文献[13]采用平衡盘结构调节了多级泵转轮后盖板腔体的压力分布,减小了轴向力。水力机械工程中,还有许多采用平衡孔或平衡盘改善轴向力特性的实例,可为本研究提供借鉴与参考[14-17]。
目前,由于结构复杂及建模困难,水泵水轮机组的轴向力CFD模拟与分析研究较少,相关研究工作有待完善。因此,本文采用计算流体动力学(CFD)方法,并结合试验研究水泵水轮机泵工况的轴向力特性。水泵水轮机的复杂结构,不利于布置平衡孔与平衡盘,为此,本文采用均压管路连接上冠腔体与尾水管,以改善机组轴向力过大的情况,为提高机组运行稳定性与安全性提供解决方案。
1 研究对象
1.1 水泵水轮机模型
以水泵水轮机真机模型开展研究,其转轮高压侧直径Dhi为4.16 m,转速nd为430 r/min,比转数ns计算公式为
(1)
式中Cns——修正系数,取3.65
Qd——泵工况设计流量
Hd——泵工况设计扬程
为方便对比分析,定义无量纲流量系数Cφ以及扬程系数Cψ为
(2)
(3)
式中H——扬程Q——流量
g——重力加速度,取9.81 m/s2
Ω——转轮旋转角速度
本例中,设计流量系数为0.043,比转数ns为115.0。水泵水轮机流域模型如图1所示。
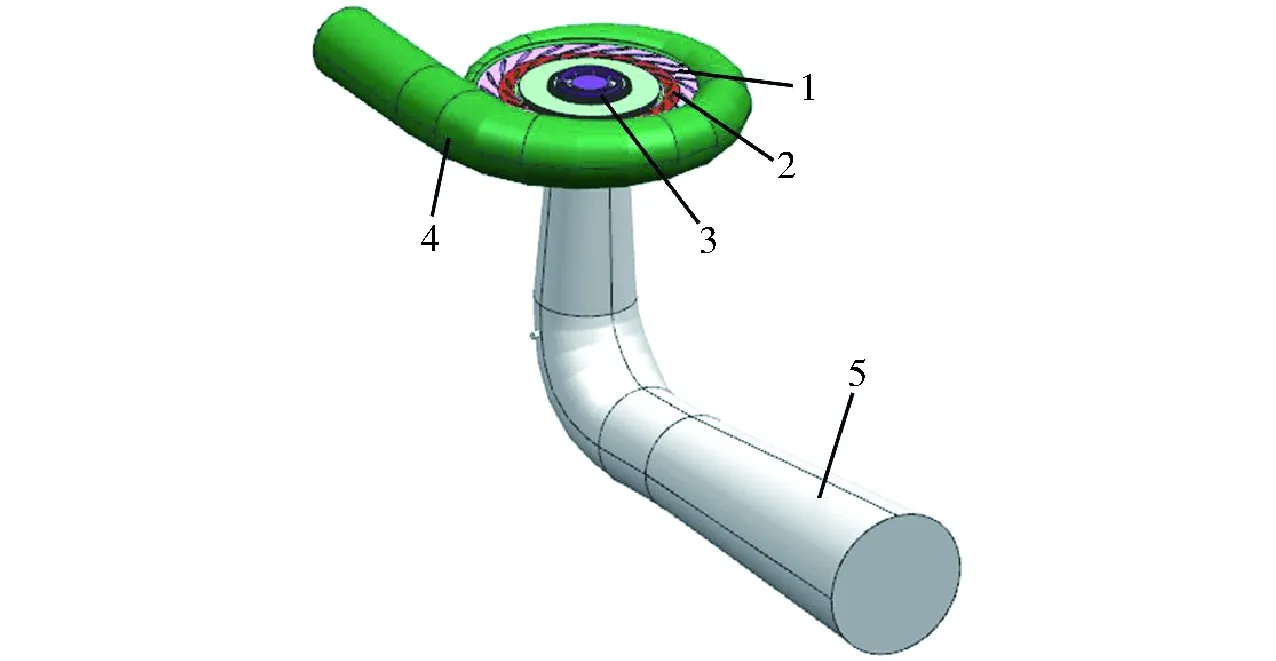
图1 水泵水轮机流域模型Fig.1 Flow passage model of pump-turbine1.固定导叶 2.活动导叶 3.转轮(含密封间隙) 4.蜗壳5.尾水管
1.2 数值模拟方法
采用CFD数值模拟方法,开展水泵水轮机内部流动的模拟和分析。在雷诺时均(RANS)方法的基础上,连续性方程、动量方程、能量方程分别写为
(4)
(5)
(6)
式中u——速度t——时间
ρ——密度x——坐标系分量
δij——Kroneker数μ——动力粘度


T——温度p——压力
hsta——静焓htot——总焓
λt——热传导系数
下角标i、j表示哑指标。由于雷诺时均湍流模拟方程的不封闭性,需引入湍流模型进行方程封闭。基于Boussinesq假设,定义涡粘性系数μt,可建立雷诺应力与平均应变率关系为
(7)
式中k——湍动能
本研究中,采用SSTk-ω模型作为湍流模型[18-19],其通过区域混合标准k-ε模型及Wilcoxk-ω模型,具有较强的可适性,能求解强逆压梯度流动及边界层强剪切流动。其湍动能k方程与耗散率ω方程分别为
(8)
(9)
式中P——湍流生成项
F1——混合方程
σk、σω、βk、Cω、σω2——模型系数
lk-ω——湍流尺度
μt——涡粘性系数,可通过lk-ω=k1/2βkω进行计算
1.3 网格划分
CFD计算前,需要对计算域进行网格划分。网格划分时采用结构/非结构单元混合网格结构,在几何规则区域采用结构网格,以节省存储空间、提高计算寻址能力。在几何不规则区域采用非结构网格,提高几何适应性,并提高网格质量,增强计算收敛性。
本研究对尾水管、转轮及其密封与间隙、活动导叶、固定导叶、蜗壳计算域分别单独划分网格。由于转轮及其密封与间隙对轴向力的计算影响显著,因此特别加密转轮及其密封与间隙部分网格。通过网格收敛性指标GCI(Grid convergence index)网格收敛性检查之后[20],确定尾水管网格节点数为34万,转轮为366万,转轮密封与间隙为589万,活动导叶为195万,固定导叶为834万,蜗壳为30万,总计2 048万网格节点。
1.4 计算设置
基于图1所示流域,计算水泵水轮机泵工况下流动。流体由尾水管流入、由蜗壳流出,因此,边界条件给定如下:尾水管进口给定为速度进口,速度取决于流量;蜗壳出口给定为压力出口,设定平均压力为1.01×105Pa;所有壁面边界设定为无滑移壁面;各部件之间采用交接面模型进行连接。
计算时,首先进行稳态计算,设定最大迭代次数为600次,收敛判据为动量方程与连续性方程残差小于1×10-5。在稳态计算结果的基础上,设定暂态计算,每个转轮周期计算360个时间步,每个时间步最大迭代次数为10次以保证收敛,收敛判据仍为动量方程与连续性方程残差小于1×10-5。稳态计算与暂态计算中,动量方程对流项的离散格式设定为高精度,湍流输运方程对流项的离散格式设定为一阶。
1.5 模型试验
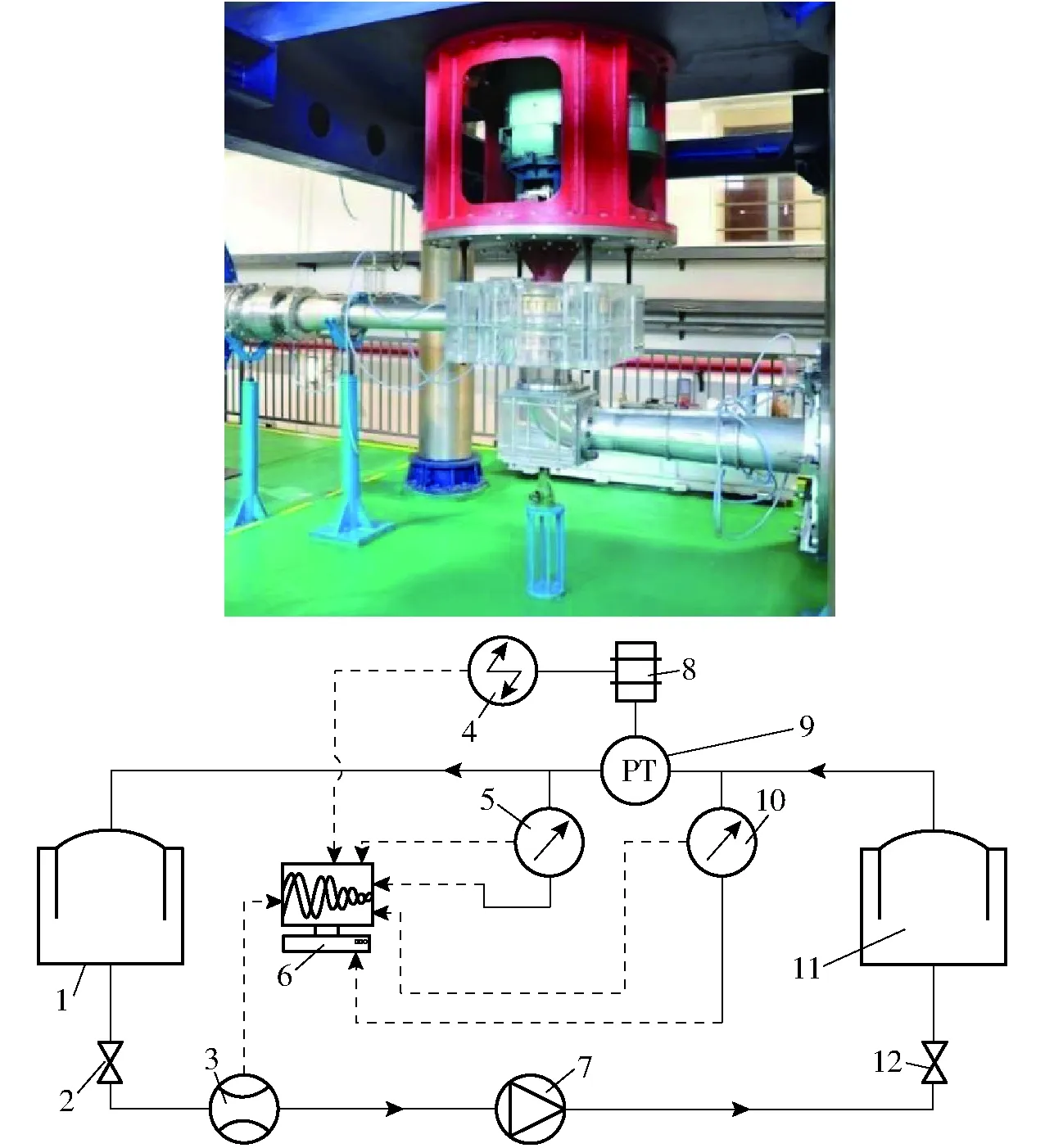
图2 水泵水轮机模型试验台Fig.2 Model test rig of pump-turbine1、11.储水罐 2、12.阀门 3.流量计 4.测功仪 5、10.压差计 6.采集卡 7.给水泵 8.电机 9.测试机组
在数值模拟基础上,采用模型试验验证机组外特性。图2为模型试验台。试验时,采用电磁流量计测量流量Q,采用压差计测量机组进出口之间压力差Δp,采用转速转矩测功仪测量轴功率N。扬程H通过H=Δp/(ρg)计算。效率η通过η=ΔpQ/N计算。最终可得机组流量-扬程(Q-H)特性以及流量-效率(Q-η)特性。
2 机组特性分析
2.1 机组能量特性
图3为活动导叶相对开度随流量系数Cφ的变化规律。其中,相对开度计算公式为
Cα=α/αmax
(10)
式中α——活动导叶开度
αmax——最大开度
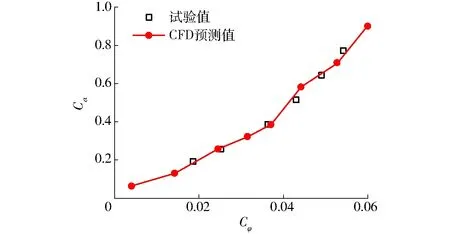
图3 活动导叶相对开度随流量系数的变化曲线Fig.3 Variation of guide vane opening with flow rate
在上述导叶开度规律下,图4对比了数值模拟与试验测试的机组能量特性曲线,即不同流量系数Cφ下的扬程系数Cψ与效率η变化曲线。
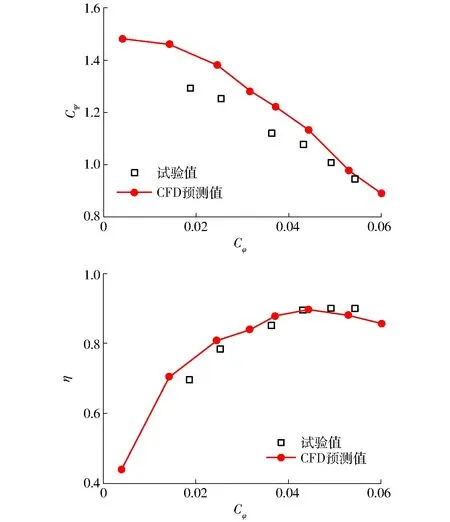
图4 扬程系数与效率随流量系数的变化曲线Fig.4 Variations of head and efficiency with flow rate
从图4可以看出,CFD模拟得到的扬程系数与效率,相比于试验值,具有相同的变化趋势。由于CFD计算未考虑圆盘摩擦损失,因此尤其在小流量下的扬程系数与效率相对较高,但属于正常范围。因此可知,CFD模拟的结果较为准确,可以作为可靠的分析工具,分析水泵水轮机内部流动及力特性。
2.2 机组轴向力特性
采用CFD预测的机组轴向力随流量系数Cφ的变化规律(负值为轴向力向下)如图5所示。其中Cfz为相对轴向力系数,计算公式为
(11)
式中Fz——转轮所受轴向力
mrn——转轮质量
图5中轴向力方向均为向下。综合图3~5可以看出,转轮所受向下的轴向力随流量减小、活动导叶开度减小、扬程上升而呈现先略微减小、后逐渐增大的趋势。
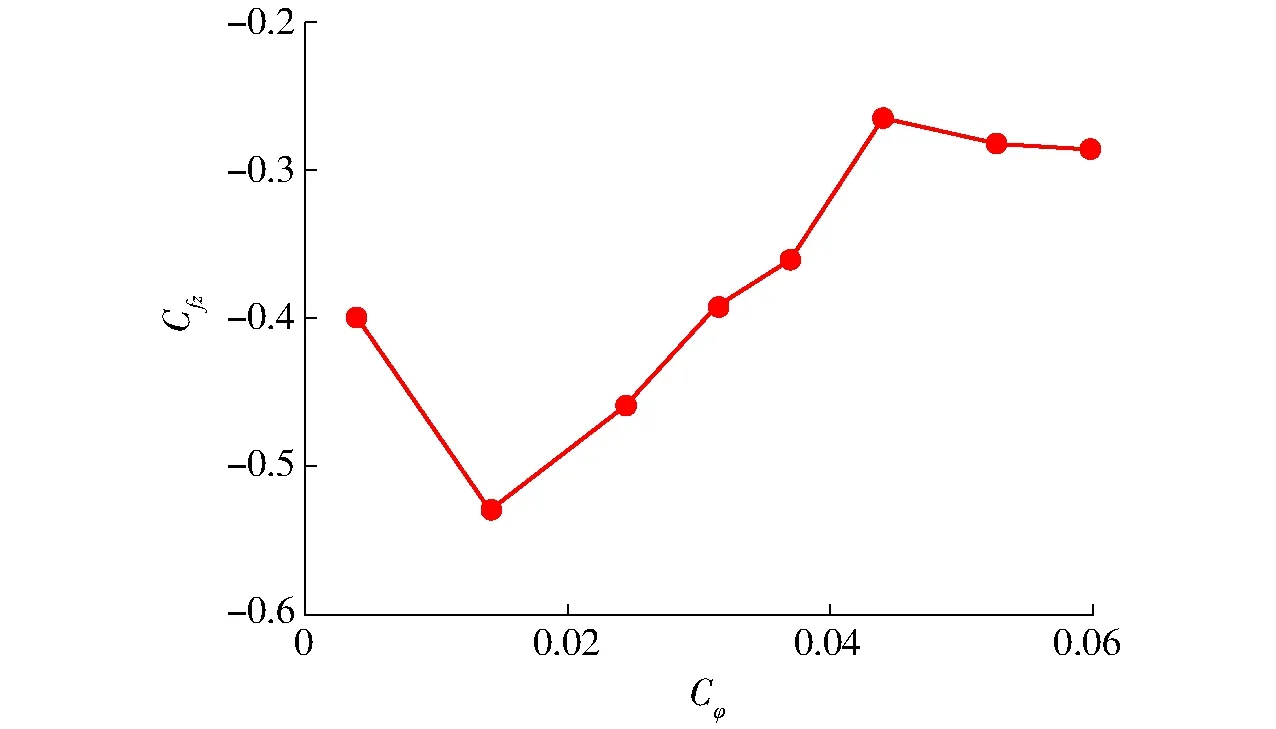
图5 转轮相对轴向力系数随流量系数的变化曲线Fig.5 Variation of runner axial force with flow rate
2.3 轴向力产生原因分析
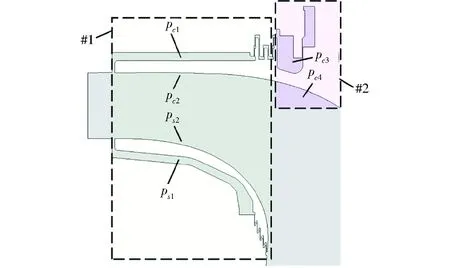
图6 转轮轴面图及上下间隙Fig.6 Meridional map of runner with indication of hub and crown leakages
图6为转轮轴面图,包含上冠与下环间隙。转轮所受轴向力的产生原因较为复杂,主要是受到上冠间隙与转轮压差、下环间隙与转轮压差的共同作用。按照图中#1与#2区域划分可知:在#1区域,上冠间隙压力为pc1,转轮相邻位置压力为pc2,下环间隙压力为ps1,转轮相邻位置压力为ps2。通常,pc1≈ps1且pc2≈ps2。因此,pc1-pc2≈ps1-ps2,即#1区域转轮轴向力平衡。反之,在#2区域,上冠间隙内压力pc3与转轮相邻位置压力pc4难以平衡,引发转轮受到向上或向下的轴向力。
当泵工况流量越小时,扬程越大,转轮出口压力越高。此时,活动导叶开度小,高压流体被限制在转轮一侧并随之流入腔体,使得pc3≫pc4,导致向下的轴向力加剧。
3 轴向力改善研究
3.1 均压管路设置
如图7所示,在上冠间隙(密封位置之后)中腔体位置引出均压管与尾水管相连,用以降低图6中#2位置的压力。均压管沿圆周方向均匀布置,每转过90°设置一根,共4根。
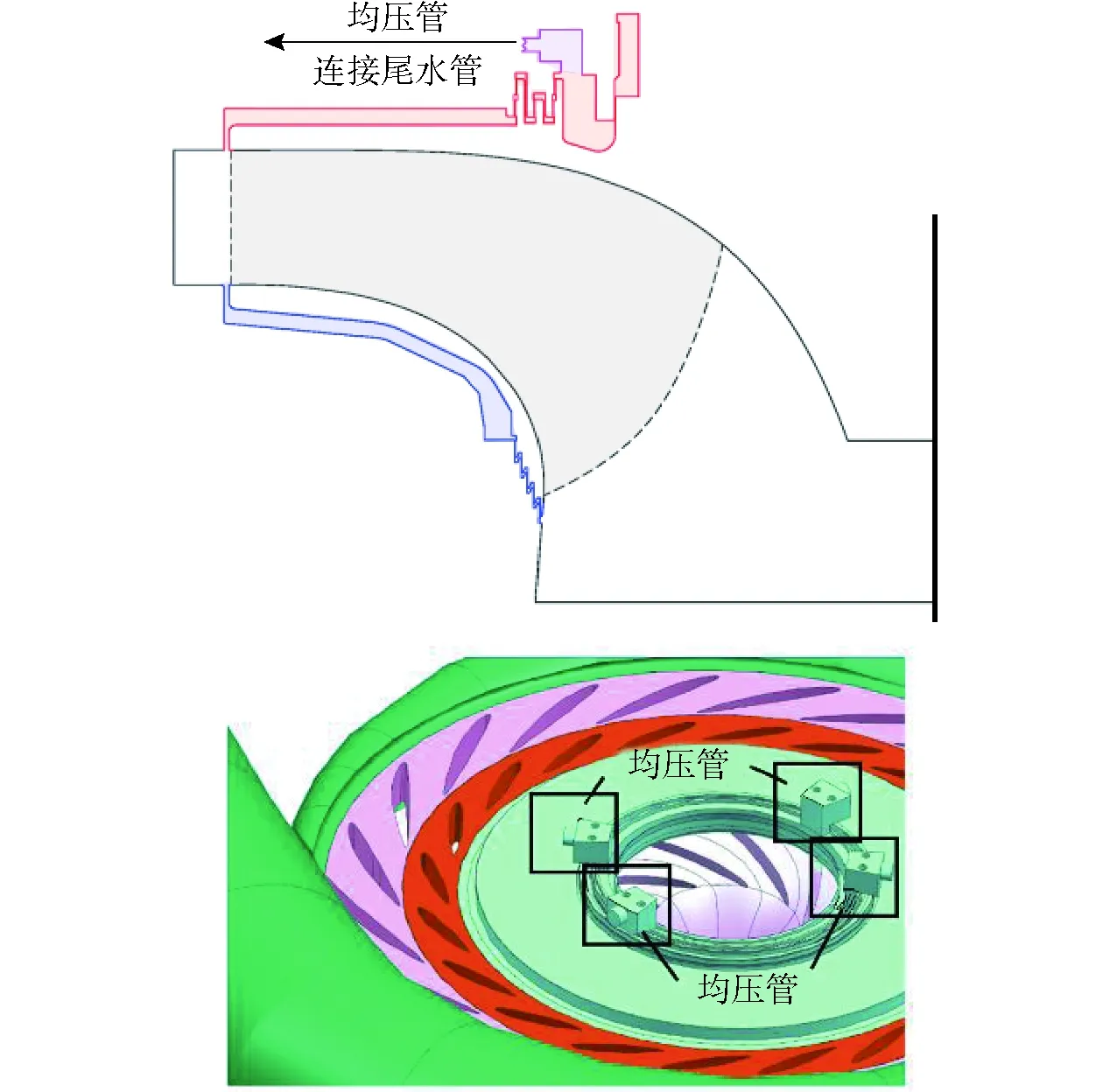
图7 均压管路布置Fig.7 Distribution of pressure balance pipelines
3.2 转轮轴向力特性改善情况
对添加均压管路之后的转轮轴向力特征进行预测,并与无均压管方案进行对比,结果如图8所示。由图可见,添加均压管之后,向下的轴向力变为轻微向上。根据相关流固耦合计算,当向下轴向力较大时,上机架支撑臂最大应力可能超过许用应力并产生塑性变形。如图8所示,改进之后,轴向力变为向上,与轴系自重相抵消之后,形成轻微向下的轴向力,避免了机架变形的风险,又不会发生抬机,机组的安全性得到显著提升。

图8 添加均压管前后转轮相对轴向力系数对比Fig.8 Comparison of runner axial force before and after setting pressure balance pipeline
3.3 轴向力改善机理验证与分析
为了验证与分析轴向力改善机理,以Cφ=0.032工况为例,对比流域内部的压力分布情况。分析采用无量纲压力系数Cp,公式为
(12)
式中pin——尾水管进口位置参考压力
从图9中可以看出,无均压管时,上冠间隙内尤其是密封后腔体内的压力极高,远高于叶轮内部相应位置的压力。此时,转轮形成向下的轴向力。反之,有均压管之后,上冠间隙内尤其是密封后腔体内的压力得到显著降低。此时,轴向力轻微向上。因此,添加均压管可以有效解决转轮向下轴向力较大的问题。

图9 Cφ为0.032时添加均压管前后压力分布对比Fig.9 Comparisons of pressure distribution before and after setting pressure balance pipeline at Cφ=0.032
4 结论
(1)基于计算流体动力学方法,考虑转轮上冠与下环间隙对机组进行建模与计算分析,可以有效预测水泵水轮机转轮的轴向力特征,为机组的安全稳定运行提供理论依据。间隙建模为解决轴向力过大的问题提供了解决方案。
(2)在水泵水轮机泵工况下,机组受到较大的轴向力。尤其在泵小流量、小导叶开度、高扬程工况时,向下的轴向力较大,易引起上机架安全隐患。轴向力产生的原因复杂,主要是由上下间隙与转轮中压力不平衡所引起。尤其在转轮增压值较大、导叶开度不足时,上冠间隙存在高压,使得向下的轴向力过大,需要平衡压差,以减小轴向力特征。
(3)在上冠间隙密封后方腔体内增加均压管路,连接尾水管低压位置,可有效均衡该处存在的高压,降低该处与转轮相邻位置的压差,有效改善较大的向下轴向力。通过设置均压管路,泵工况轴向力转变为轻微向上,在不发生抬机风险的前提下,机组承重部件结构强度问题得以有效解决。
——“AABC”和“无X无X”式词语

