无人机侦察图像运动模糊复原方法研究

武永恒，张小孟2，李小民，李文广2，李 炭

(1.石家庄铁道大学 电气与电子工程学院，石家庄 050043; 2.陆军工程大学石家庄校区 无人机工程系，石家庄 050003)

0 引言

无人驾驶飞机简称“无人机(unmanned aerial vehicle，UAV)”，是利用无线电遥控设备和自备的程序控制装置操纵的不载人飞机[1]，是各国战略打击中不可缺少的军事力量。无人机侦察成为信息化战争中获取情报的重要手段，可根据获取到的战场信息及时对敌方行动展开有效对抗。

无人机在侦察过程中会受到诸多因素使图像降质，而降质图像使后期利用图像进行情报分析变得困难，导致情报的失准、片面化，进而影响决策者的正确判断及战争的胜负，降低了侦察图像的应用价值。其中运动模糊图像最容易形成，如何降低运动模糊图像对后期情报处理的影响成为无人机侦察图像预处理的关键。因此，对图像运动模糊复原算法进行研究具有重要意义。

本文对无人机侦察图像运动模糊的成因及特点进行简要概述，并对现在主流的两类运动模糊复原方法(运动非盲复原法与盲复原法)进行了深入研究，针对无人机侦察图像的特点分析了每种算法的性能，最后对无人机侦察图像实时去模糊的发展趋势进行了展望。

1 无人机侦察图像运动模糊成因及特点

1.1 无人机侦察图像运动模糊成像原因

无人机在飞行过程中，由于载荷的复杂振动和相机抖动等因素导致航拍器成像面(CCD)的移动速度与拍摄图像像素的移动速度不同步，即相机在曝光时间内拍摄物体与感光介质之间发生相对运动，使实际成像在CCD上产生位移而形成运动模糊图像，产生原理如图1所示。

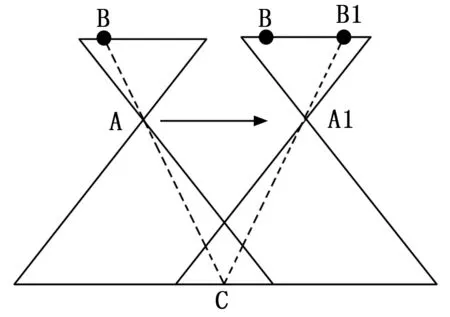
图1 运动模糊产生原理

无人机从A点飞行到A1的过程中：无人机在A点时，地面上的一点C会在CCD上的B点成像(理论成像位置)，当无人机运动到A1时，地面上的点C成像在B1(实际成像位置)，C点的成像由B点移动到B1点，产生水平位移，形成运动模糊。

1.2 无人机侦察图像运动模糊成像特点

无人机在情报获取过程中，图像大多是高空垂直拍摄，这使无人机侦察模糊图像相对于其它模糊图像具有自身特点：

1)无人机飞行高度较高且运动速度快，航拍图像的模糊尺度较大。

2)图像内目标数量大，有河流、山丘、浅色建筑等，影响去模糊效果。

3)无人机运动方式有匀速运动、正弦运动、随机运动等，不同运动方式拍摄的模糊图像有各自的特点。

4)高空垂直拍摄，使得拍摄图像含不确定噪声影响去模糊效果。

2 图像非盲复原法

非盲复原法是在图像的点扩散函数(point spread function(PSF)，模糊核)和模糊图像已知的情况下建立图像退化模型，然后对模型进行逆运算得到清晰图像的一种方法。这种方法出现较早，相对现有的新方法来说比较完善，但应用在无人机侦察领域时存在以下问题：

1)由于无人机航拍图像的不确定性，使得无法确定图像的模糊核，失去已知条件无法建立退化模型。

2)针对性较差，没有针对无人机运动模糊特点进行处理，复原效果不理想。

常用的方法有：逆滤波算法、维纳滤波算法、约束最小二乘算法、Lucy-Richardson算法。

2.1 逆滤波算法

逆滤波法使用傅里叶变换将图像的退化模型转换到频域来求解原始图像[2]。图像的退化模型描述为一个空间域的卷积过程，退化模型的表现形式为[3]：

g(x,y)=h(x,y)*f(x,y)+n(x,y)

(1)

式中，g(x,y)为模糊图像，h(x,y)为模糊核，f(x,y)为清晰图像，n(x,y)为噪声，*是卷积运算。将式(1)通过傅里叶变换可得到频域退化模型：

G(u,v)=H(u,v)F(u,v)+N(u,v)

(2)

式(2)可变形为：

(3)

在忽略噪声的情况下，式(3)中第二部分为零，仅根据模糊图像与模糊核即可求得复原图像。

20世纪60年代中期，Nathan使用逆滤波法恢复太空中获取的模糊图像，但效果较差[3]。随后Harris[4]与Mcglamery[5]对逆滤波法进行了改进，分别使用PSF解析模型和由实验得到的PSF对模糊图像进行复原，效果稍有改善，但当噪声较大时仍无法得到清晰图像。

逆滤波法虽简单快速，但有很大的局限性：实际情况下模糊图像必定会存在噪声，当噪声较大时式(3)中第二部分的值与理想情况相差较大，无法复原出清晰图像。因此逆滤波法只适用于噪声较小甚至可以忽略的情况，并不适用于无人机侦察这一背景。

2.2 维纳滤波算法

由于逆滤波法抗干扰性较差，1967年Helstrom改进了逆滤波，提出将图像和噪声看作是一个随机过程，以未退化图像和估计图像之间的最小均方误差来复原图像的维纳滤波算法[6]。均方误差度量式如下：

(4)

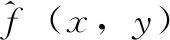
(5)

式中，G(u,v)是模糊图像的傅里叶变换，G*(u,v)是G(u,v)的共轭，且|G(u,v)|2=G*(u,v)G(u,v)，Sn(u,v)是n(x,y)的功率谱，且Sn(u,v)=|N(u,v)|2，Sf(u,v)是f(x,y)的功率谱，且Sf(u,v)=|F(u,v)|2，γ的取值代表滤波器的种类：γ=1时，为标准维纳滤波器；γ为随机变量时，为含参数维纳滤波器；当噪声很小可以忽略(Sn(u,v)=0)时，式(5)退化为逆滤波器。

实际中一般将噪声视为高斯白噪声，式(5)近似表示为：

(6)

式中，K为常数，通过人为调节K的值来使均方误差最小，复原出理想图像。当K增大时，滤波器加强对噪声的抑制使复原图像变暗；当K减小时，滤波器减小对噪声的抑制使复原图像质量下降。大量数据表明K取[0.001,0.01]时复原效果较为理想。

1967年，Slepian[7]将维纳滤波法推广到处理随机模糊核的情况。之后Pratt[8]与Habibi[9]将算法进行优化，提高了维纳滤波的计算精度和速度，但其复原效果并不理想。1974年，卡农[10]提出了类似维纳滤波的功率谱均衡滤波器，在特定情况下，得到了较为清晰的复原图像。随后Hunt[11]将此方法应用在噪声较大的模糊图像上时发现，维纳滤波出现了低通滤波效应，人工痕迹明显，图像失真严重。

维纳滤波法在一定程度上抑制了噪声的影响，但并不适用于无人机侦察领域，主要原因归结为三点：

1)维纳滤波只适用于线性系统，而实际中的成像往往都是非线性的。

2)人类视觉系统中的平滑效应与维纳滤波复原出图像的平滑效应相差较大。

3)算法存在病态问题，且抗噪性较差，无法复原出清晰图像。

2.3 约束最小二乘算法

为克服维纳滤波法的病态问题，提出一种依靠噪声均值和方差的先验知识求解最优值的方法，即约束最小二乘法[12]。

约束最小二乘法在图像复原模型上增加约束条件，使原始图像二阶导数的二范数最小(即‖f″‖2最小)，以达到复原图像的目的。为了方便计算将二阶导数替换为二阶差分，把问题转化为求‖Qf‖2的最小值，其中Q为f的线性算子。原始图像f满足图像的退化模型式(1)，得到其约束条件：

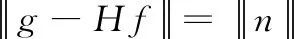
(7)

由此，根据Lagrange乘法建立数学模型：

(8)

其中:λ为拉格朗日系数。最后解得：

(9)

根据实际中不同种类的模糊图像，寻找相应的先验知识，确定线性算子Q的取值，建立出不同形式的约束最小二乘算法，找到求解病态问题的方案，复原出清晰图像，这是约束最小二乘法最大的优点。但其跟逆滤波法有相同的缺点，在噪声较小可以忽略时复原效果较为理想。当噪声的强度过高时，复原效果过于依赖λ的取值，当λ过小时噪声对复原图像影响较大，当λ过大时人工痕迹过于明显，目前为止还未找到合适的取值。而且该方法需根据不同种类模糊图像，人工找寻合适参数后进行复原，不适用于情报侦察。

2.4 Lucy-Richardson算法

Lucy-Richardson算法区别于上述三种算法，它是一种非线性的迭代复原方法，它是由Lucy和Richardson分别提出，引用时通常称为Lucy-Richardson(简称L-R)算法[13]。L-R算法是基于贝叶斯框架和泊松分布的一种数学模型，依靠统计模糊信号的震荡概率特性，将问题转化为求解模型的最大似然估计值来复原图像。

贝叶斯公式：

(10)

式中，P(x|y)表示在事件y的条件下事件x发生的概率，P(y|x)表示在事件x的条件下事件y发生的概率，P(x)表示事件x的概率。

泊松统计模型：

(11)

式中，u表示给定时间范围内事情发生的平均次数。

根据贝叶斯公式和泊松统计模型得到L-R算法的迭代方程：

(12)

当模糊图像中仅存在泊松噪声时，L-R算法复原效果较为清晰，但随着迭代次数n的增加，图像的失真现象会越来越严重。

L-R算法存在振铃效应降低了复原图像的质量，因此学者们对L-R算法进行了改进。J.J.Ding等人[14]将金字塔结构融入L-R算法，将图像的模糊尺度细化后再进行迭代复原，减少了迭代次数，一定程度上避免了细节引起的振铃效应。D.Chen等人[15]基于多高斯光束模型和基尔霍夫近似，估计了模糊图像的点扩展函数，进一步提高了L-R算法复原图像的清晰度。H.Zhao等人[16]提出了一种基于矢量外推法的L-R算法，在算法的框架中引入一个指数修正项，使迭代步骤加大、算法收敛速度变快，但噪声放大速度较快，且信噪比较低。由于L-R算法运算量较大、需反复试验、只对存在泊松噪声的模糊图像复原效果较好等缺点，导致L-R算法并不适用于无人机侦察图像复原。

3 图像盲复原法

无人机进行侦察时图像会受到噪声等不确定因素的影响，无法确定图像的点扩散函数，使得图像非盲复原法不再适用。图像盲复原法针对这种随机不确定问题，利用仅有的模糊图像来寻找先验知识，建立数学模型，复原模糊图像[17-19]。根据复原策略的不同，图像盲复原主要分为先验辨识法和联合辨识法两大类[20]。

3.1 先验辨识法

先验辨识法利用模糊图像的先验知识对PSF进行估计，把图像盲复原问题转化为图像的非盲复原，再利用非盲复原算法进行处理。常见的方法有：空域法和频域法。

3.1.1 空域法

空域法是根据图像模糊前后边缘的变化来估计退化参数的一种方法。对模糊图像中退化参数的估计是模糊图像复原的关键，在建立退化模型中如何获取更好、更精确的退化参数一直是图像复原的研究重点，其准确性直接影响去模糊效果。

根据图像边缘的这种特性，Lin等学者[21]研究了一种检测模糊核模糊尺度的方法，通过运动模糊图像在运动方向上梯度的变化估计出图像边缘的扩散宽度，得到模糊尺度的近似值，由于梯度测量的缺陷使得模糊尺度的精度较低。加州大学的Bae H等人[22]将Kinect体感设备与IMU传感器应用到摄像机中设计了一个可以估计模糊核的设备，提高了模糊核参数的精度。由于模糊图像在空域中的特征并不明显，因此近年来对该方法的研究较少。

3.1.2 频域法

频域法是根据模糊图像在频域中的特征估计模糊核的一种方法。Cannon等学者[23]发现了匀速直线运动模糊图像的频谱上存在一条零值条纹，根据条纹可计算出模糊核，但其受噪声影响较大，复原效果并不理想。Lokhande等学者[24]通过检测模糊图像频谱中暗条纹的方向，得到模糊角度。华中科技大学邓泽峰博士改进了Radon变换法，提出了基于Radon变换的极大值算法和基于曲线拟合的反比例模型法[25]分别计算模糊角度和模糊尺度。但在有噪声时，效果较差。A.M.Deshpande等人[26]提出了一种将倒谱域法与位平面切片法相结合的方法，提高了模糊核参数估计的精度。

频域法虽然简单、快速，但其对存在加性噪声的图像复原效果并不理想，而且此方法仅限于匀速直线运动模糊图像，另外频谱中没有零值条纹则无法估计模糊核。由于获取先验知识的条件过于复杂，缺乏一般性使得该方法不适用于无人机侦察这一背景。

3.2 联合辨识法

联合辨识法是将模糊核估计与图像复原结合，同时进行处理的一种方法。该方法实用性、鲁棒性较强，但算法复杂，实时性较差。常见的方法有：迭代盲反卷积法、非负支持域约束递归逆滤波法和基于正则化的方法。

3.2.1 迭代盲反卷积法

迭代盲反卷积法(iterative blind deconvolution, IBD)是图像盲复原中最直接有效的一种算法[27]。该方法根据PSF与模糊图像在频域和时域中的特点，在频域与时域之间交替迭代求解，直至满足一定标准。

交替求解时需对PSF与模糊图像添加约束条件：像素的非零性与模糊核的能量守恒性。此约束条件下的复原图像模型表示为：

(13)

式中，N为像素总数。像素个数随着迭代次数的增加而减小，当N为零时停止迭代。通过傅里叶变化和维纳滤波算法得到IBD迭代公式：

(14)

(15)

式中,Sff(u,v)，Shh(u,v)，Snn(u,v)分别是原始图像、PSF和噪声的功率谱，其比值可用较小的常量代替。

IBD法虽然简单直观，但由文献[28]分析可得IBD法与维纳滤波相似抗噪性较差，而且解的唯一性和收敛性无法确定。为此屈志毅等人[29]先使用IBD法对点扩散函数进行估计，然后采用神经网络的方法复原，保证了算法的收敛性。但在迭代求解过程中受模糊图片中的噪声级别和模糊程度影响较大，无法保证复原质量。张雯雯等人[30]提出了一种多尺度的迭代卷积法，该法将图像分解到平滑分量和细节纹理分量，然后分别对每个分量进行迭代卷积求解，提高了复原图像的质量。至今IBD法虽有了很大改善，但对噪声干扰的鲁棒性依然较差。

3.2.2 非负支持域约束递归逆滤波法

非负支持域约束递归逆滤波法(nonnegativity and support constraints recursive inverse filtering，NAS-RIF)是一种逆滤波的方法，算法流程如图2所示。

图2 非负支持域约束递归逆滤波算法流程

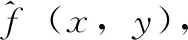
本方法充分利用高通滤波器的特性，求取全局函数的最小值。但又由于高通滤波器，将噪声放大导致图像的清晰度下降。针对NAS-RIF算法的不足，文献[31]在非线性限制函数中添加边缘保持约束项，提高了图像的纹理细节，但只针对信噪比低的图像具有较好的复原效果。文献[32]首先使用轮廓去噪法削弱图像的噪声，再使用NAS-RIF算法进行复原，提高了图像的信噪比。文献[33]使用几何非线性扩散滤波除去了部分噪声，又将总变分引入非线性限制函数，在保持图像细节的情况下提高了图像的信噪比，但当噪声较为严重时复原质量会大大降低。因此NAS-RIF算法对于含不确定噪声的无人机侦察图像来说并不适用。

3.2.3 基于正则化的方法

基于正则化的方法是根据PSF与模糊图像的特点构建相应的正则化约束来复原图像。基于正则化方法的图像复原框架可表示为：

(16)

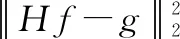
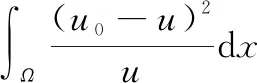
基于正则化的方法相对其他方法具有稳定、细节突出、良好的抗噪性等优点，但仍无法满足无人机侦察过程中实时去模糊的要求，因此基于正则化的方法成为无人机模糊图像复原领域研究的热点。

4 实验与分析

4.1 数据采集

本实验采用模拟运动模糊图像与无人机拍摄的真实运动模糊图像验证算法的复原效果。模拟运动模糊图像是清晰图像与PSF卷积后加入高斯噪声得到。图3是测试图像Cameraman、Woman及对应的模糊核与模糊图像。

图3 测试图像

无人机拍摄的真实运动模糊图像取自DJI Phantom 3 Professional 型无人机，如图4所示。

图4 无人机拍摄的真实运动模糊图像

4.2 复原实验

实验对象如表1所示。

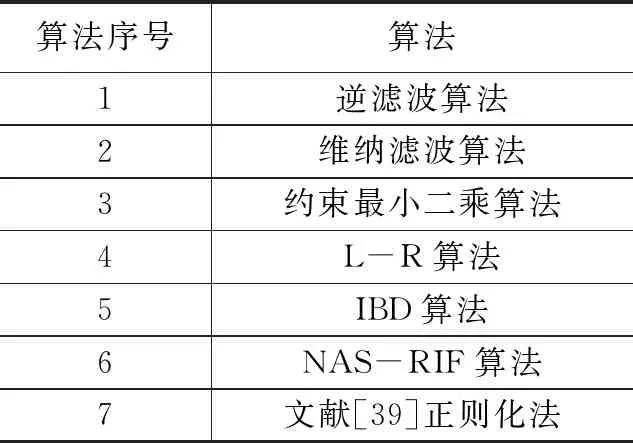
表1实验对象

为验证正则化法的鲁棒性与实用性首先利用7种算法对测试图像Cameraman与Woman进行复原实验。然后进行无人机运动模糊图像复原实验，将NAS-RIF算法与文献[38]正则化法进行对比分析。

图5是算法1～7的复原效果对比图，对比发现盲复原法较非盲复原法复原图像更清晰。对比(f)、(g)、(h)发现正则化法复原的模糊图像主观视觉更好，图像边缘清晰程度较好。

图5 模糊图像复原效果对比图

图6 无人机运动模糊图像复原效果

由于算法1～5复原效果较差，对无人机运动模糊图像仅对算法6与算法7的复原效果进行对比。如图6所示。

由图6中的(b)、(c)分析可得：较NAS-RIF算法，正则化法复原图像整体对比度更好，图像清晰度更好。由图6中的(d)、(e)、(f)分析可得：正则化法复原图像纹理细节更加明显，减少了重影现象。

通过实验表明正则化法应用于无人机运动模糊图像时复原效果较好，相对于其他算法实用性较强。

5 结束语

随着计算机视觉与人工智能技术的发展，对无人机侦察信息处理的要求不断提高。因此，针对无人机在运动过程中产生的降质图像，在分析目前主流算法的基础上，根据无人机侦察图像自身的特点，对无人机侦察图像运动模糊复原算法的发展趋势做出以下展望：

1)提高算法的处理速度。处理速度在情报处理中要求较高，而目前复原算法无法在保证复原质量的前提下实现快速处理。

2)提高算法的适用性。目前复原算法大都针对某类图像具有较好的复原效果，而无人机侦察环境复杂多变使得图像信息具有不确定性，因此提高算法的适用性成为无人机侦察图像复原领域中的重要研究方向。

3)提高算法的智能性。理想的智能算法是可根据实际情况智能选择参数，高效的完成处理。而现有算法是经多次实验由经验得到合适参数或手动调节参数，因此复原算法的智能性是目前无人机图像处理领域亟待解决的问题。