基于Q学习的供热末端自适应PID控制算法
(西安建筑科技大学 信息与控制工程学院,西安 710055)
0 引言
近年来,随着我国城市规模的快速发展和城镇化率的提高,北方城市市政集中供暖建筑面积不断增加,随之而来的是建筑供暖能耗的快速增长。当前,建筑供暖末端的调节阀多为手动调节阀,且大多处于“全开”和“全关”的运行状态,这种“全开”和“全关”的控制方式一方面给用户带来不良的热舒适体验,另一方面也造成建筑供暖能量的大量浪费。因此,建筑供暖节能存在巨大潜力,而如何实现供暖末端的高效调控,既是改善供暖室内环境热舒适性、降低建筑能耗的关键,也是集中供暖系统节能亟待解决的问题。
针对集中供暖系统与供暖末端的调控问题,国内外学者开展了大量研究,如I.H.Yang[1]等人研究了人工神经网络(ANN)在供暖系统中的应用,针对温控系统的时间滞后问题,采用ANN来估算供暖系统的启动时间以加快系统响应,提高用户的热舒适性;L.Z.Li[2]等人采用6种不同的混合控制策略对锅炉系统的燃油燃烧速率、热水流量和热水温度进行控制,取得了近17%的节能效果;徐宝萍[3]等综述及评价了国内外末端控制相关研究情况,提出了突破单一用户室温控制、兼顾供暖系统水力工况及回水温度变化的系统优化控制思路;王娇[4]等采用模糊控制理论,设计了根据各参数隶属度函数及参数调节规则的自校正模糊控制器;李琦[5]等在分析集中供热系统运行机理的基础上,建立热源总热量生产优化问题的数学描述,利用双启发式动态规划(DHP)算法和质量并调的控制策略求解,获得热源供水流量和供水温度的优化设定值;刁成玉琢[6]等采用实验研究方法对比分析了风机盘管、顶板辐射、侧墙辐射、地板辐射4种不同供暖末端时的室内温湿度、空气流速和壁面温度等数据,获得了4种供暖末端的热舒适性结论。上述研究取得了许多积极成果,对本文研究的开展具有较好的借鉴意义。
比例-积分-微分(PID)控制以其结构简单,鲁棒性好和工作可靠性高的特点而在控制领域得到了广泛应用,但传统PID 的参数一旦确定就无法在线调整,难以满足时变系统的控制要求,如何高效地调整和优化PID的控制参数成了人们竞相研究的问题。近年来兴起的强化学习为PID参数自适应调整提供了新的思路和方法,并取得了较好的应用效果[7-10]。本文在分析现有研究成果的基础上,以PID控制算法为基础,针对集中供暖末端控制系统存在大滞后、强耦合的特点,引入强化学习算法,提出一种基于Q学习的PID参数在线优化的供暖末端流量控制算法,旨在利用Q学习算法对PID 参数进行整定与寻优,从而获得更优的控制参数,并在仿真实验中验证该方法的有效性和节能效果。
1 PID控制器
典型的PID控制器原理如图1所示。
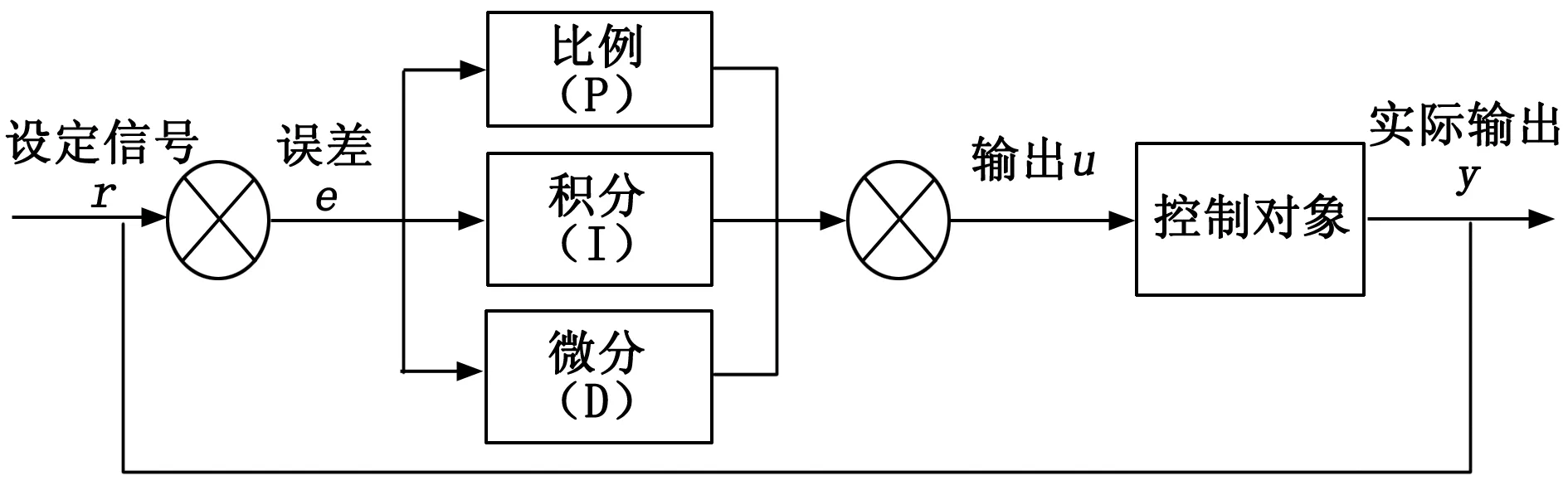
图1 PID控制系统原理图
典型的PID控制系统由控制器、被控对象和反馈回路组成。PID控制器根据设定值和实际输出值之间的偏差,对偏差进行同比例放大(或缩小)、积分以及微分后,通过线性组合构成控制量,进而对被控对象进行控制,其控制规律如下:
(1)
式中,e(t)=r(t)-y(t)为控制量;Kp为比例系数;KI为积分时间常数;KD为微分时间常数[11]。
2 供热末端的热平衡模型
由传热学理论可知,供热末端—采暖房间的热平衡方程可表示为:
Q=Q得-Q失
(2)
式中,Q得为采暖房间总得热量,即散热器散热量;Q失为采暖房间总失热量,主要包括房间维护结构传热耗热量Q1和门窗缝隙渗入的室外空气吸热量Q2;Q为采暖房间的最终热量,且有:
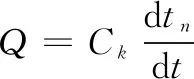
(3)
式中,Ck为采暖房间空气的热容,Ck=c1·ρ1·V,ρ1为室内温度下的空气密度,其取值一般通过查询《传热学附表》可得。
散热器释放热量为:
Q得=Gcp(tg-th)
(4)
式中,tg为散热器进口热水温度(℃);th为散热器出水口热水温度(℃);G为散热器进水流量(m3/s);cp为热水比热。
室内外通过围护结构传递的热量为:
(5)
式中,tn为用户室内当前温度(℃);tw为户外温度,S为围护结构的传热面积(m2),k1为围护结构(外墙)的平均传热系数(W/m2·℃),L为墙体厚度m。
室内外空气对流换热量为:
Q2=λ·ν·ρ2·c2(tn-tw)
(6)
式中,λ为单位换算系数,1 KJ/h=0.278 W;v为门、窗缝隙渗入室内的总空气量(m3/h),v=M×H×β;其中:M为每米门、窗缝隙渗入室内的总空气量(m3/h·m),H为门、窗缝隙的计算长度(m),β为修正系数,根据《供热工程》附录查阅可知西安地区渗透量的修正系数为0.7。ρ2为冷空气的定压密度,c2为冷空气的定压比热。将式(3)~(6)代入式(2)可得:
ρ2·c2(tn-tw)
(7)
式(7)即为供暖房间的热平衡数学模型。由式(7)可知,当供暖房间面积、围护结构参数等确定后,散热器入口流量决定室温变化率,由于室温设定值为人为设置,则通过控制流量大小控制房间温度变化。
3 基于Q学习的自适应PID算法
3.1 强化学习
强化学习算法(RL算法)是机器学习的一个重要分支,其区别于深度学习中的有监督学习和无监督学习,通过试错与环境交互获得策略的改进,进行自学习和在线学习[12]。其受到大脑学习本质的启发,只通过智能体与环境交互而不知道系统模型的基础,模拟动物学习行为过程中大脑的学习过程,通过智能体(即实际运用中的传感器)与环境条件相互作用获得先前数据,独立自主进行动作选择,生成控制策略,不断循环,使智能体具有自主学习能力。强化学习过程如图2所示,智能体(Agent)不断与环境(environment)进行信息交互。智能体Agent感知环境当前状态St∈S,根据初始策略施加一个动作at∈a给环境Environment,环境在该动作的作用后,更新状态为St+1∈S,同时根据奖惩计划提供一个奖励或惩罚以更新策略,然后智能体Agent再次感知环境新状态St+1∈S选择新的动作at+1∈a,直到到达终端状态ST∈S。智能体Agent的目标就是获得最大化奖励的概率下得到一个最优控制策略。

图2 RL中智能体-环境交互的图示
强化学习是一种基于马尔可夫决策过程的无模型增量式动态规划,其属性为:t时刻状态信息足够以供智能体Agent进行决策生成t+1时刻动作,从而决定进行决策t+1时刻状态[13]。假定环境的所有可能状态是一个有限状态的离散马尔可夫过程,强化学习系统对每一步动作的选取为单步进行,环境在接受动作后便发生状态转移,并得到评价函数,其中状态转移的概率为:
(8)
策略π下给定状态下的状态值函数定义为:
(9)
其中:γ∈(0,1]是权衡下一步回报率的折扣因子,Eπ表示策略π下的期望值。因为在动态规划中至少得保证有一个策略π*,并有:
Vπ*(st)=max{r(π(st))+γ∑P[st,at,st+1]Vπ*(st)
(10)
类似的,在策略p下的状态s中采取动作a的动作值函数Qπ可以定义为:
Qπ(s,a)≐Eπ[Gt│St=s,At=a]=
(11)
在所有动作值函数中,最佳动作值函数定义为:
Qπ*(s,a)≐maxπQπ(s,a)
(12)
式中,π*为最优策略,当策略为π*时,动作函数值Qπ(s,a)最大。在最佳动作值函数最大时的π*为最优策略,根据生成的最优策略π*,确定最优PID增益(Kp(t),Ki(t),Kd(t))进行室温控制。
3.2 Q学习算法
Q学习算法是一种基于时间差分方法的无模型控制算法,是RL领域最重要的进步之一[14]。Q学习使用状态-动作值函数Q(St,At)来查找最优策略π*,动作值函数Q(St,At)的定义如下:
Q(St,At)=Q(St,At)+α[Rt+1+
γmaxaQ(St+1,a)-Q(St,At)
(13)
式中,α∈(0,1]是学习率。Q学习算法的伪代码如算法1所示。
算法1:Q学习算法
Step1:初始化任意Q(s,a),∀a∈A,∀s∈S;
Step2:循环所有epsode;
重复
Step3: 更新状态St;
重复
Step4: 执行动作At,观察St+1和Rt+1;
Step5: 根据式(13)更新Q值;
Step6:St←St+1;
Step7: 直到St达到最终状态ST;
Step8: 直到episode 结束。
3.3 供热末端自适应PID控制器设计
基于Q学习的供热末端自适应PID控制系统结构如图3所示,包含PID控制器和学习Q表两个部分。PID 控制器实现供热流量的调节,控制器参数Kp,Ki,Kd通过在线学习的Q表进行自适应调整。
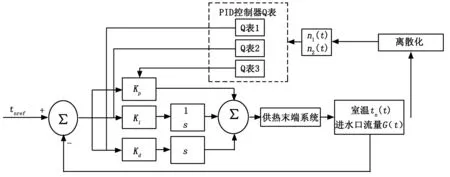
图3 基于Q学习PID的供热末端系统控制器结构
室温设定值tnref作为输入,将室温tn(t)与设定值的偏差作为控制量,进行PID控制。便于数据采样,将室温tn(t)和进水口流量G(t)离散化得到n1(t)和n2(t)作为状态,进行Q学习,生成3个Q表,每个Q表分别与PID控制器的比例增益Kp、微分增益Ki和积分增益Kd相对应,当给定当前状态时,每个学习的Q表生成PID控制器增益的最佳值。
3.4 结合Q学习的PID控制算法
本文中基于Q学习PID的关健是对PID增益参数Q表的训练,通过Q表将不同环境状态映射到不同的PID的增益上。为加快Q表学习过程,采用了适应模型参数的启发方式——Delta-Bar-Delta[15]自适应学习率方法。训练出当前状态下最优的PID增益后,根据式(2)~(7)计算出控制量u(t),在控制量作用后再观察新状态下的流量和室温,比较前后时刻状态获得奖励Rp,并继续进行训练学习,不断通过观察状态训练Q表,得出每个状态下的PID增益以控制阀门开度改变环境状态。故结合Q学习PID控制算法的伪代码如算法2所示。
算法2:结合Q学习的PID控制算法
Step1:初始化任意Qi(s,a)=0,∀a∈A,∀s∈S,i=1,2,3…6;
Step2: 更新学习率a1和a2;
Step3: 更新ε-greedy策略的ε;
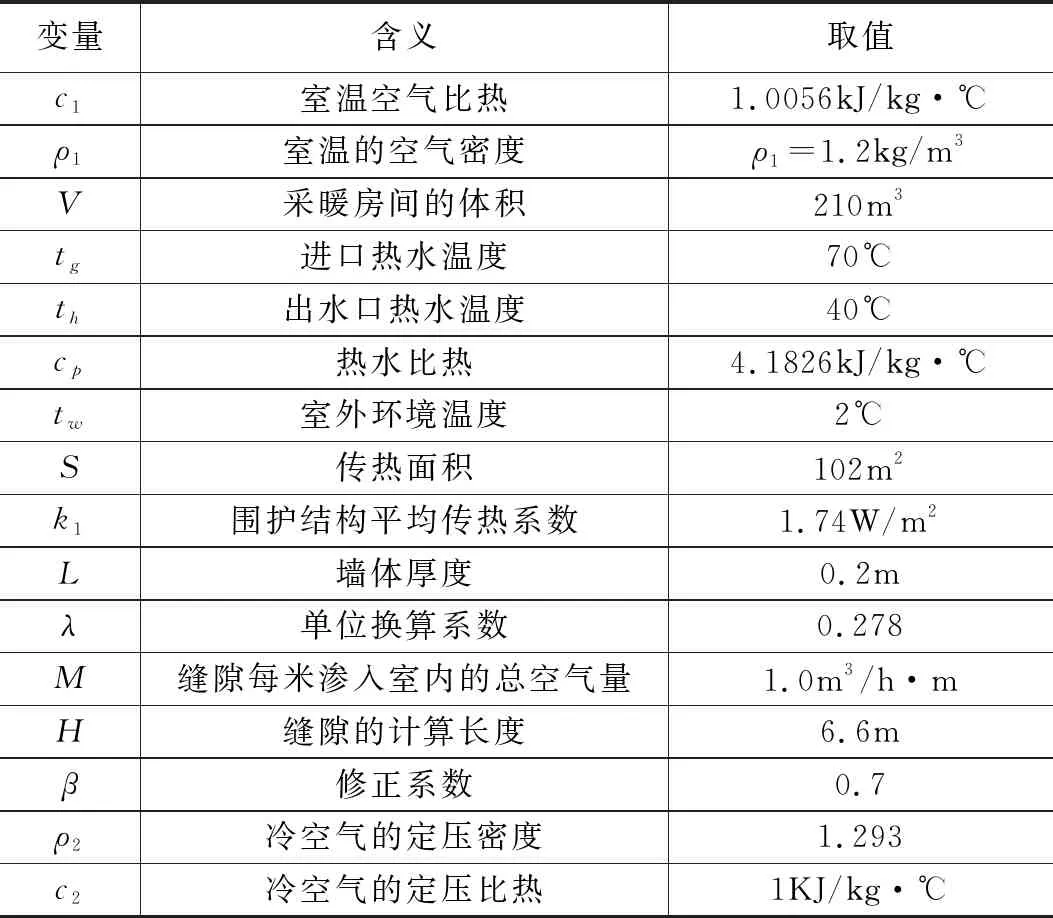
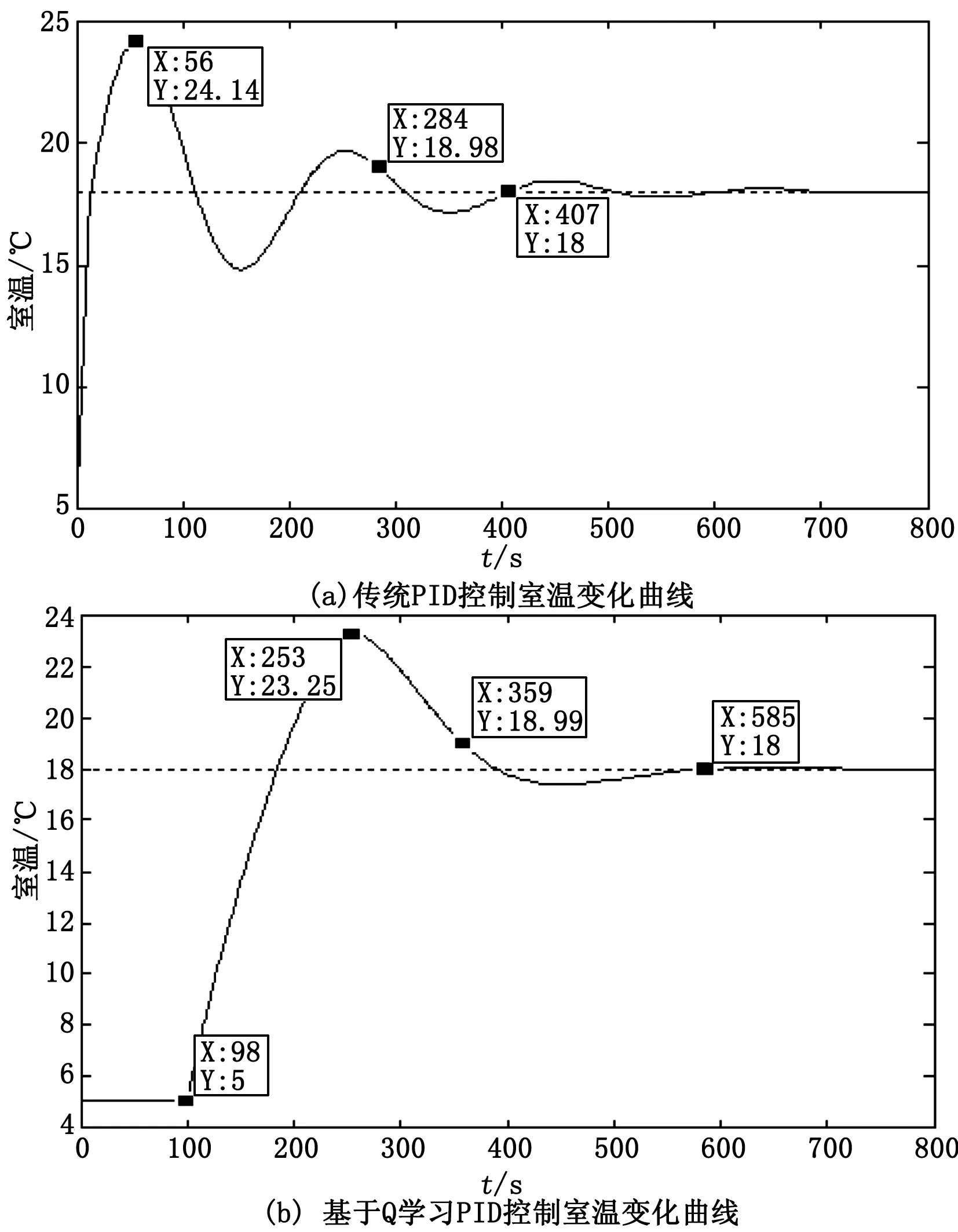
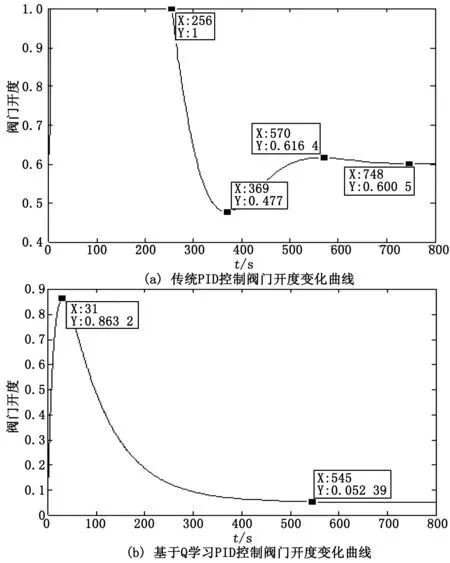
Step4: 当episode Step5:t=0; Step7: ε衰变,(当episode>0.6×maxepisode,ε=0); Step8: fort=1;t≤maxtime,t++; Step9: 将St离散化,获得:n1(t),n2(t); Step10: fori=1;i≤3,i++ Step11: 根据n1(t),n2(t)选择动作Ai,遵循ε-greedy政策; end Step12: 根据式(2)~式(7),获得完整的输出u(t); Step13: 观察新状态St+1(tn(t+1),G(t+1)); Step14: 获得Q1(s,a),Q2(s,a)和Q3(s,a)的奖励Rp; Step15: 将St+1离散化, 获得:n1(t+1),n2(t+1); Step16: 更新Q1(s,a),Q2(s,a)和Q3(s,a)的学习率α1; Step17: 用Rp和α1更新Q1(s,a),Q2(s,a)和Q3(s,a); Step18:St←St+1; End End 3.4.1 离散化 为加快训练速度,对于效果相同的情况可为同一控制参数进行调节,故将每个连续变量被分成几个区间,同一区间内的值被视为一个相同的状态。使用相同的规则设置存储区间定义为: (14) 其中:[x]=max{n∈Z|n≤x};n表示离散变量;xcon表示连续变量;Xmin和Xmax分别是xcon的下限和上限;N表示每个变量被分成的区间数,在这种情况下N=10。区间的数量取决于模拟性能。 本文需将室内温度tn和阀门开度K通过式(14)区间划分进行离散化处理,离散化设定的值如表1所示。 表1 系统离散化约束 3.4.2 ε-greedy方法 为保证奖励最大化,采用当前Q值最大的动作,因为在ε-greedy策略中,ε的值越大,表示采用随机的一个动作的概率越大。故当给定当前状态时,三个Q表都根据ε-greedy方法生成动作,此方法被定义为: (15) 式中,ξ∈[0,1]是一个正态分布的随机数。 (16) 其中:eps是当前episode,而maxepisode是episode的最大值。 3.4.3 奖励策略 奖励策略根据应用实际情况而定。本文根据室内供热末端系统将奖励函数分为3种情况:调控后室温趋于设定温度,室温远离设定温度,室温无变化。 1)调控后室温趋于设定温度。根据at得到的增益调控所得室温tn(t)与设定值T设的差值小于t-1时刻室温tn(t-1)与T设的差值,即说明此次调控有效,给予其调控所达效果的奖励值,即为前后时刻室温变化值。 2)调控后室温远离设定温度。根据at得到的增益调控所得室温tn(t)与设定值T设的差值大于t-1时刻室温tn(t-1)与T设的差值,即说明此次调控为干扰调控,奖励负值。 3)调控后室温无变化。根据at得到的增益调控所得室温tn(t)与设定值T设的差值等于t-1时刻室温tn(t-1)与T设的差值,即说明此次调控无效,即不奖励不惩罚。 所以奖励计划如下: r(t)= (17) 3.4.4 自适应学习率 为了提高收敛效率,采用Delta-Bar-Delta[15]自适应学习率算法。算法定义为: (18) 当学习速率变得太大时,学习速率的增加改变符号并降低学习速率。另一方面,如果学习速率太小,则学习速率在先前趋势中保持变化并加速收敛。所以本文通过将当前TD误差与先前步骤中的累积TD误差进行比较来更新学习速率,即时间步骤t+1中的学习速率为: αt+1=αt+Δαt (19) 实验环境为西安地区高3 m,宽7 m,长10 m的供暖房间,故采暖房间体积为V=210 m3,窗户为1 800 mm×1 500 mm单层金属窗,其墙体主要为钢筋混凝土制造,墙体厚度为L=0.2 m,查阅《供热工程》附录可知,钢筋混凝土围护结构(外墙)的平均传热系数为k1=1.74 W/m2,西安地区空气渗透量修正系数β=0.7。根据我国《采暖通风与空气调节设计规范》查阅,设定温度设置为18℃,西安城区冬季未供暖下平均室温为5℃,即实验中初始室温为5℃。仿真实验中各参数变量的取值如表2所示。 将表2实验环境数据代入式(7),可得到: (20) 整理得到: (21) 将式(21)拉氏变化可得: (253.4112s+889.0607)Tn(s)=125.478G(s)+1778.1214 (22) 表2 实验环境参数取值 由于本文仅考虑热水流量控制对室温调节的影响,即当实验环境确定时,即房间结构参数、室外温度和室内初始温度确定时,供暖房间的热平衡数学模型如式(22)所示。 本文在Simulink中搭建室内热平衡模型,在Matlab中利用传统PID和基于Q学习的改进PID算法对模拟实验环境下的供热末端控制系统式(22)进行仿真。分别比较了其输出量室温和控制量阀门开度的变化,也比较了控制过程中热水总流量,并且从系统的性能指标上进行了对比。 对比图4可以看出,调节过程中基于Q学习PID控制的室温变化明显比传统PID控制策略超调量更小,所以其在热量利用率会相对更高;其振荡次数更少,人体对室温的舒适度更好。不过基于Q学习改进PID控制策略使室温达到稳态的时间较长,其主要原因是基于Q学习实现PID参数在线调节的过程中数据计算量大。 图4 室温变化仿真结果 在开度调节方面,对比图5可以看出基于Q学习改进PID控制策略下的阀门开度变化更加平缓,其调节过程中所需要的供热流量为G总=626.1836 m3,而传统PID控制策下阀门调节后,整个控制过程所需的供热流量为G总=934.421 m3,基于Q学习的自适应PID控制系统节约了32.99%的供热量。从阀门损耗角度而言,对阀门的损耗会更小,阀门使命寿命也会得到增长。 图5 开度变化仿真结果 为了更精确分析两种控制策略的控制效果,结合室温变化仿真结果做了控制性能指标分析。 表3 控制性能指标分析 根据控制性能指标分析可知基于Q学习改进PID的控制策略稳态时间在9.75 min,传统PID控制策略稳态时间在6.78 min,考虑实际情况下,15 min内达到设定温度可以满足供热用户的需求。 由于室内供暖过程中突变环境较为复杂频繁,如当室温达到设定值后,由于外来人员的突然闯入或开窗使得外来冷空气渗入导致室内温度骤降等。为得知基于Q学习PID控制策略在环境突变下的控制效果,本文在t=800 s时,室内温度发生突变骤降为14℃后,比较基于Q学习PID控制策略和传统PID控制策略的控制效果,仿真结果如图6所示。 图6 环境突变下室温变化仿真结果 针对集中供热末端流量调节的PID控制参数优化与节能问题,首先依据传热学理论分析和推导了散热器、围护结构和室内外空气对流换热的热动态过程和传热过程,建立了供热房间的热平衡数学模型,在此基础上,以优化PID参数和供热末端节能为目标,提出了基于Q学习在线优化PID参数的供热末端流量控制算法,设计了自适应PID控制器,实现了PID参数的在线整定。最后通过仿真实验验证了所设计PID控制器的调控性能并与传统PID控制结果进行了对比,仿真实验结果表明,所提方法能够实现室内温度和调节阀开度的平缓调控,且能节省约33%的供热量。当发生突变后,基于Q学习PID控制策略的振荡也优于传统PID,初始温度-设定温度-发生突变-设定温度整个过程,基于Q学习的自适应PID控制系统能耗减少了30.02%。在保证室内环境的热舒适性的基础上对降低建筑供热能耗具有重要的意义。
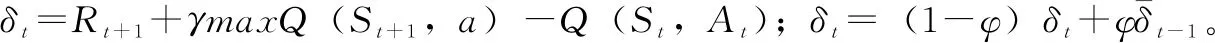
4 仿真实验
4.1 仿真环境
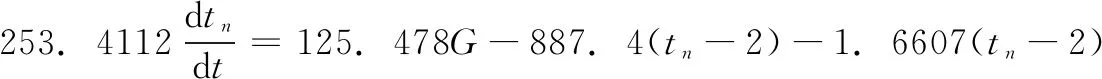
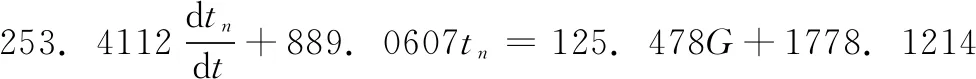
4.2 实验结果分析



5 结束语

