基于深度图像先验的散焦图像去模糊

摘  要：在散焦模糊图像中单个像素的模糊量由其景深确定，因此散焦模糊是空间变化的。传统的去模糊方法在解决这种空间变化的反卷积问题的时候，会在不同散焦程度的边界处产生明显的振铃效应。针对上述存在的问题，文章提出了基于深度图像先验的散焦图像去模糊算法。实验结果表明，与现有的散焦图像去模糊算法对比，该算法具有更好的去散焦模糊的性能。

关键词：散焦图像;去模糊;振铃效应;深度图像先验

中图分类号：TP391       文献标识码：A 文章编号：2096-4706（2020）24-0084-05

Defocused Image Deblurring Based on Depth Image Prior

CHEN Tianming

（College of Electronic and Information Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing  210016，China）

Abstract：In a defocused and blurred image，the blur amount of a single pixel is determined by its depth of field，so the defocus blur is spatially variable. When traditional deblurring methods are used to solve the deconvolution problem of this kind of spatial variation，obvious ringing effect will appear at the boundary of different defocus degrees. Aiming at the above problems，this paper proposes a defocused image deblurring algorithm based on depth image prior. Experimental results show，comparing with the existing defocused image deblurring algorithm，this algorithm has better defocusing and deblurring performance.

Keywords：defocused image;deblurring;ringing effect;depth image prior

0  引  言

在人們使用照相机等成像设备获得目标图像的过程中，由于光学成像系统的浅景深导致的散焦模糊，是影响图像视觉质量的一个重要因素。为了从散焦模糊图像中恢复出清晰图像，通常有两种途径来实现，即光学方法和数学方法。其中光学方法会使得摄像系统复杂化，而且付出的成本与收益不成正比。相反，数学方法因其低廉的成本和便捷性逐渐成为主流，呈现出巨大的发展潜力。由于散焦模糊是空间变化的。这种空间变化反卷积问题的现有解决方案是，首先将输入图像分割成近似均匀模糊量的几个区域，然后在每个区域上分别进行反卷积恢复出清晰图像。

将深度卷积神经网络应用于散焦图像去模糊的一个困难是，网络的训练需要提供大量的原图像，这很难实现。最近，Ulyanov等人[1]发现卷积神经网络结构本身具有捕获单个图像低维信息的能力，由此提出了无需预先训练就可用于图像恢复的深度图像先验（Deep Image Prior，DIP）算法。受到DIP算法的启发，本文提出了一种基于深度图像先验的散焦图像去模糊算法。通过对估计出的散焦图进行分割，得到具有多个不同参数的模糊核。通过不同散焦区域的掩膜运算，并且采用Structural Similarity（SSIM）损失函数，使得网络训练时能够学习生成清晰图像。

1  算法实现原理

散焦图像的去模糊主要分为三个步骤进行。首先对散焦模糊图像进行模糊度的估计，得到散焦图。然后通过对散焦图区域分割，生成多个模糊核。最后在DIP网络的框架下恢复出清晰图像。本文对第一步散焦图的生成，不做探讨，而是运用Xu等人[2]提出的散焦模糊图的估计算法。

1.1  散焦模糊核的生成

在散焦图像中，模糊量与景深有着密切的关系。由于场景深度在空间上是存在差异的，在图像的不同位置，估计出的模糊量是不同的，也就是说模糊核在空间上是变化的。为了保证局部区域场景深度的均匀性，通过将散焦图分割成多个区域，并将每一个区域内所有像素的模糊量平均值作为该区域的散焦模糊量，由式（1）表示：

（1）

其中，n为分割出的区域标签，σn和mj分别为第n个区域的散焦模糊量大小和第j个像素的散焦模糊量大小，Mn为第n个区域的范围，t为在Mn范围内总共的像素个数，l为总共划分出的区域个数。由此，第n个区域的模糊核定义为：

（2）

其中，x和y为坐标。这样，我们将空间变化的盲去模糊问题转化为一个局部区域空间不变的非盲去模糊问题。分别对每一块区域进行恢复，并对结果进行拼接，最终得到清晰的图像。如图1所示，图1（a）是模糊图，图1（b）是通过算法[2]估计出的散焦图，根据一定的阈值分割，从而得到图1（c）。计算每一块分割区域内像素的平均值，把这个值作为模糊核的参数σn，从而得到每一块区域的模糊核，如图1（d）所示。

我们对于一张清晰Lena图的四个不同区域卷积四个不同参数的高斯核，如图2（a）为清晰图，图2（b）为四个不同大小的高斯核，从而得到具有不同模糊程度的散焦模糊图像，如图2（c）。再分别用对应的高斯核，采用超拉普拉斯先验的快速图像反卷积算法[3]和本文提出的去模糊算法，实验结果如图3（a）和图3（b）所示。

通过观察图3的去模糊结果，传统的算法在具有不同散焦量的图像边界上，存在很明显的振铃效应，而本文提出的散焦图像去模糊算法则能恢复出良好的清晰图像。

1.2  基于深度图像先验的散焦图像去模糊算法

本文考虑散焦图像由多个深度层组成的情况，每一层都是由清晰图像部分和散焦模糊核卷积的结果，也就是说，散焦模糊的图像可以按照以下方式建模：

（3）

其中，⊙为元素对应乘积操作符，?为卷积操作符。L为区域个数，对于第i层来说，αi为二进制区域掩膜矩阵，位于该层的像素，其值为1，否则为0。ui为相应的清晰图像部分，ki为与第i层关联的模糊核，f为输入的模糊图像，n为图像噪声。最后的输出则是一幅清晰图像，用  表示，形式为：

（4）

在本文中，αi是通过使用算法[2]估计出的散焦图上进行分割后得到的。ki是上节散焦模糊核的生成中得到的。本文提出的基于深度图像先验的散焦图像去模糊算法，网络结构如图4所示，图像生成网络x被用来捕捉清晰图像的深层先验信息，并且只使用输入的噪声进行训练，其输出层采用非线性Sigmoid来约束x中的像素在[0，1]之间。

图4公式中，?为损失函数，z为输入噪声，x为清晰图像，y为输入的散焦图像。

清晰图像通常包含显著的结构和丰富的纹理，这就要求生成网络x具有足够的建模能力。我们采用DIP网络，即带跳跃连接的编码器-解码器网络作为x。如图4所示，编码器的前5层被跳跃连接到解码器的后5层。图5所示展示了某一单元的编码器-解码器结构。最后，利用卷积输出层产生最终的清晰图像。

利用上述生成网络x，并且我们引入额外的TV正则化器和正则化参数来考虑模型中的噪声水平，通过结合x和TV正则化来捕获图像的先验信息，损失函数采用SSIM，由此我们可以将模型公式化为以下形式：

（5）

其中，αi为第i层的二进制掩膜矩阵，位于该层的像素，其值为1，不在该层的像素，值为0。⊙为元素对应乘积操作符，ki为第i层的模糊核，zx为输入的噪声，y为输入的散焦模糊图像，λ为正則化参数。

式（5）的优化过程可以解释为一种“零次学习”的自我监督学习，其中生成网络x仅使用模糊图像y来进行训练，而不是通过真实的清晰散焦图像库训练。算法过程为：

算法1：基于深度图像先验的散焦图像去模糊算法

输入：模糊图像y，散焦区域矩阵αi，散焦模糊核ki

输出：清晰图像x

从均匀分布中取样噪声zx

For t = 1 to T do

;

计算x的梯度

使用ADAM优化算法和式（5）更新

End

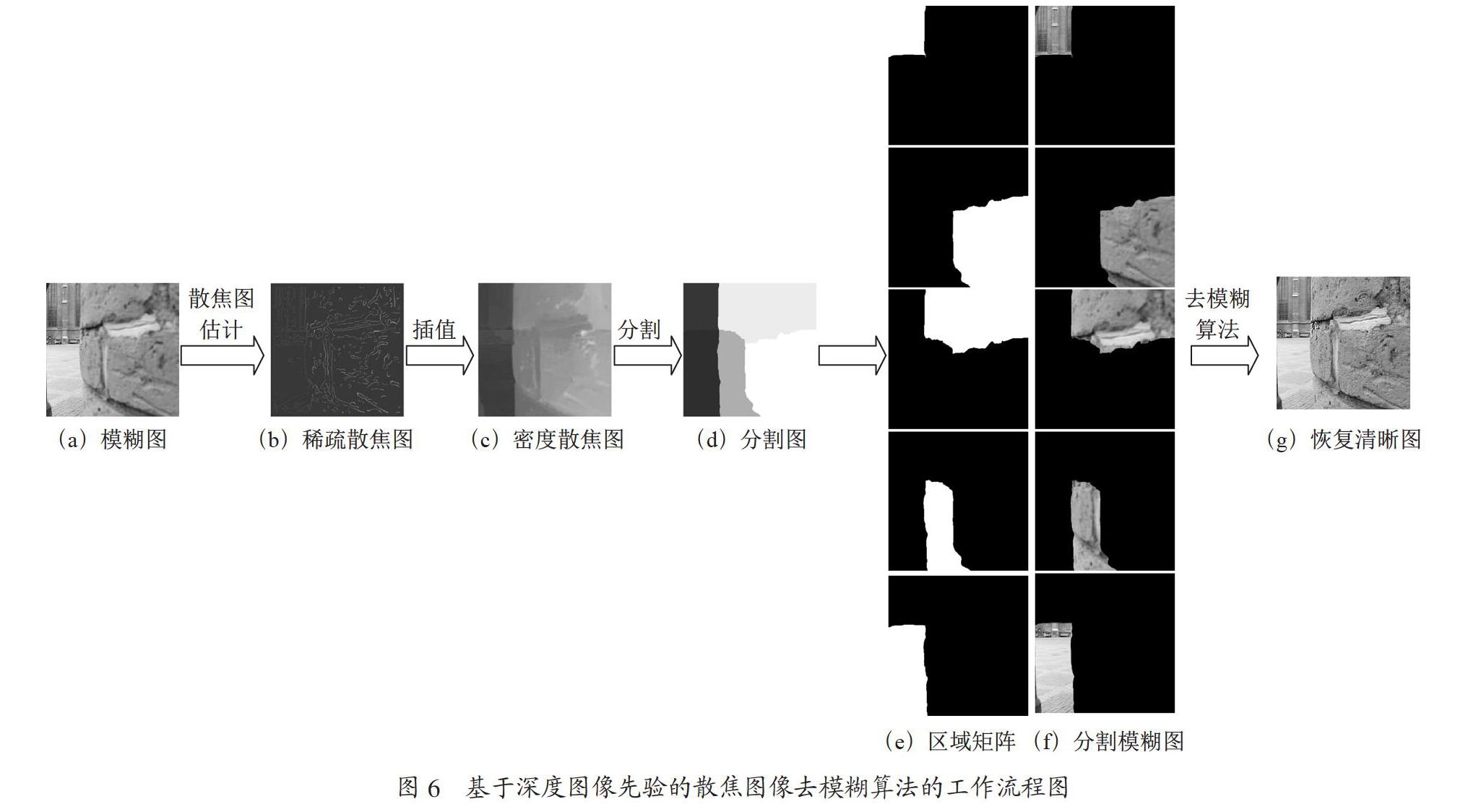
图6所示是本文提出的基于深度图像先验的散焦图像去模糊算法的工作流程。输入一幅模糊图，如图6（a），首先使用散焦模糊图估计算法[2]，得到图6（b）稀疏散焦图，进而通过插值获得图6（c）密度散焦图。然后通过在散焦图上进行阈值划分，将密度散焦图分割成多个区域，并将每一个区域内所有像素的模糊量平均值作为该区域的模糊量，由此生成多个模糊核{ki}。并且根据阈值分如图6（e）和图6（f），将输入图像分为i个不同的散焦层，得到区域矩阵{αi}，最后使用本文提出的散焦图像去模糊算法，得到图6（g）清晰图像。

2  实验结果

在对比实验中，我们使用了DAndrès等人[4]最近提出的具有已知散焦模糊值的数据集，该数据集具有22张自然散焦图像。通过采用Zhuo[5]，Tang[6]，Zhang[7]，Karaali[8]提出的算法和本文提出的算法将得到的去模糊图像与清晰图像进行比较。我们通过比较去模糊图像的质量Peak Signal to Noise Ratio（PSNR）和Structural Similarity（SSIM）指标来评判算法的性能。各个算法的去模糊效果指标如表1所示。

通过上表可以观察到，只有本文的方法在平均PSNR和SSIM指标上，相较于原模糊图像，指标呈正增益。另外我们还比较了Karaali的去模糊算法和我们的去模糊算法，在用真实散焦图情况下的去模糊效果，我们的指标要明显优于Karaali。由此验证了本文提出的基于深度图像先验的去模糊算法是具有显著优势的。从中选取五张散焦模糊图像及不同算法恢复出的清晰图像进行展示，实验结果如图7所示。

3  结  论

本文提出了一种基于深度图像先验的散焦图像去模糊算法。该算法解决了应用传统反卷积方法到散焦图像的去模糊中所存在的明显的振铃效应现象。并且通过对比其他散焦图像去模糊算法，验证该算法表现出更好的去模糊性能。由于该算法依赖于散焦图的估计，从而得到多个模糊核，属于非盲反卷积。后续工作中需要设计一种盲反卷积，通过迭代的方法同时估计出模糊核和清晰图像。

参考文献：

[1] LEMPITSKY V，VEDALDI A，ULYANOV D. Deep Image Prior [C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition.Salt Lake City：IEEE，2018：9446-9454.

[2] XU G D，QUAN Y H，JI H. Estimating Defocus Blur via Rank of Local Patches [C]//2017 IEEE International Conference on Computer Vision（ICCV）.Venice：IEEE，2017：5381-5389.

[3] KRISHNAN D，FERGUS R. Fast Image Deconvolution using Hyper-Laplacian Priors [C]//NIPS09：Proceedings of the 22nd International Conference on Neural Information Processing Systems.Vancouver：Curran Associates Inc，2009：1033-1041.

[4] DANDR?S L，SALVADOR J，KOCHALE A，et al. Non-parametric Blur Map Regression for Depth of Field Extension [J].IEEE Transactions on Image Processing，2016，25（4）：1660-1673.

[5] ZHUO S J，SIM T P. Defocus map estimation from a single image [J].Pattern Recognition，2011，44（9）：1852-1858.

[6] Tang C，HOU C P，Song Z J. Defocus map estimation from a single image via spectrum contrast [J].Optics Letters，2013，38（10）：1706-1708.

[7] ZHANG X X，WANG R G，JING X B，et al. Spatially variant defocus blur map estimation and deblurring from a single image [J].Journal of Visual Communication and Image Representation，2016，35（3）：257-264.

[8] KARAALI A，JUNG C R. Edge-Based Defocus Blur Estimation With Adaptive Scale Selection [J].IEEE Transactions on Image Processing，2018，27（3）：1126-1137.

作者簡介：陈天明（1995—），男，汉族，江苏启东人，硕士研究生，研究方向：数字图像处理。