带式输送机液粘软起动装置动力传递机理研究*

李彬彬

(中国煤炭科工集团 太原研究院有限公司，山西 太原 030032)

0 引 言

目前，在煤矿井下会布置多条采煤工作平面，且多个工作平面大多采用带式输送机传递运输物[1-3]。因输送距离远，输送量大，矿用的带式输送机是高效煤矿高产的关键装备[4-5]。

对于矿用带式运输装备，大负载导致的大惯性增加了装备软起动难度。目前，有关软起动技术的研究主要包括机械软起动和电机软起动两大类。其中，机械软起动有液力耦合器软起动和液粘软起动等；电机软起动通过改变电机结构或电源特性，例如变频器调速和串级调速[6-7]。

液粘软起动相比较于其他3种方式在适应性以及节能方面都具有一定的优势。本文分析液粘软起动装置的结构及软起动过程传递转矩的规律，利用MATLAB对软起动过程中的油膜动态特性进行分析，以期为以后的液粘软起动装置的设计与应用提供指导。

1 结构及工作原理

1.1 液粘软起动装置结构

液粘软起动装置结构如图1所示[1]。

图1 液粘软起动装置结构1-推进油缸；2-从动轴；3-控制油口；4-弹簧；5-从动轴透盖；6-主动片；7-对偶片；8-冷却油口；9-主动轴透盖；10-主动轴；11-支撑盘

液粘软起动装置工作时，控制油口通入控制油；推进油缸压力提高时，活塞推动主动摩擦片向被动摩擦片方向靠近，油膜厚度减小，粘性剪切力增大，输出转矩增大；控制系统压力降低时，活塞推力减小，弹簧将主被动片分隔开，油膜厚度增大，粘性剪切作用减小，输出转矩减小；润滑油液由冷却油口进入到摩擦片和对偶片之间，在摩擦副之间形成动态剪切油膜，起到冷却、润滑和传递动力的作用。

1.2 液粘软起动装置的传动机理

根据牛顿内摩擦定律，离合器内部的一对摩擦副可以简化为计算模型[9-10]，如图2所示。

图2 液粘传动工作原理示意图

其传递转矩可表达为：

(1)

式中：M—传递转矩，N·m；n—摩擦副组数，组；μ—动力粘度，Pa·s；h—油膜厚度，m；r1—摩擦副内径，m；r2—摩擦副外径，m；ω1—主动轴转速，rad/s；ω2—被动轴转速，rad/s。

2 软起动过程

带式输送机因输送带本身的特性，其理想的起动过程应该符合以下条件[11]：

(1)起动时间足够的长，使得在起动过程中的速度达到规定速度；

(2)起动时的最大加速度较小；

(3)加速度的突变小。

因此，软起动可以使得驱动设备平顺的输送载荷给输送带，保证输送带的平稳运行。

2.1 理想起动曲线

目前，软起动过程有两种常见的方式[12-13]，分别为Harrision和Nordell起动，其起动曲线表达式分别为：

(1)Harrision起动曲线：

(2)

(2)Nordell起动曲线：

(3)

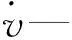
根据起动曲线的表达式，通过求解可得到起动曲线，如图3所示。

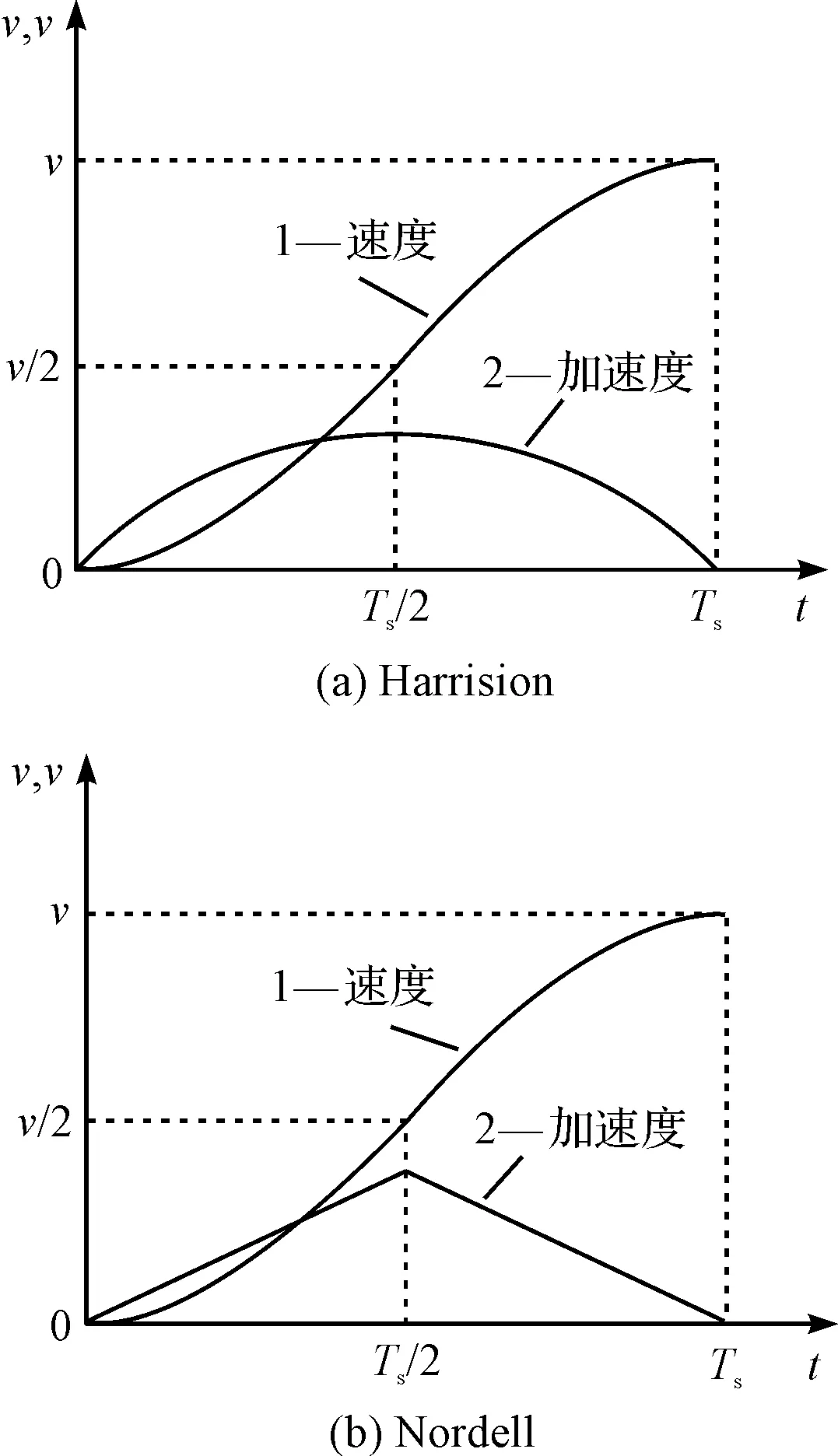
图3 Harrision和Nordell起动曲线

Harrision起动曲线：起动时的加速度数值为0；当时间到Ts/2时，加速度达到最大值，然后逐渐减小；当速度达到额定值时，加速度减为0；其加速度可由速度曲线的一阶导数求得。

Nordell起动曲线：起动时的加速度也为0；当时间到Ts/2时，加速度达到峰值，然后逐渐减少；当速度达到额定值时加速度减为0。

Harrision起动曲线又称最小加速度起动曲线，Nordell起动曲线又称最小冲击起动曲线[14]。两种曲线在实际中都有应用，但由于Harrision起动曲线无加速度突变，在实际应用中被更多地采用。本文即将采用该起动速度曲线对调速起动过程进行机理分析。

2.2 液粘软起动分析

本文选用带式输送机理想起动曲线计算，软起动采用液粘软起动，液粘软起动过程中，其缓冲过程主要靠液压系统的闭环控制来完成[15-16]。

根据式(1)可知，液粘传动调速起动装置传递转矩M是输出转速ω2和油膜厚度h的函数，传递的转矩与油膜厚度一一对应。因此，研究油膜变化的动态特性对研究液粘装置的软起动具有重要的参考价值。

3 油膜动态数值分析

3.1 模型建立

本文以迪卡尔坐标系研究油膜的状态，为简化计算，选取油膜的1/15作为研究对象。

所建立的模型如图4所示。

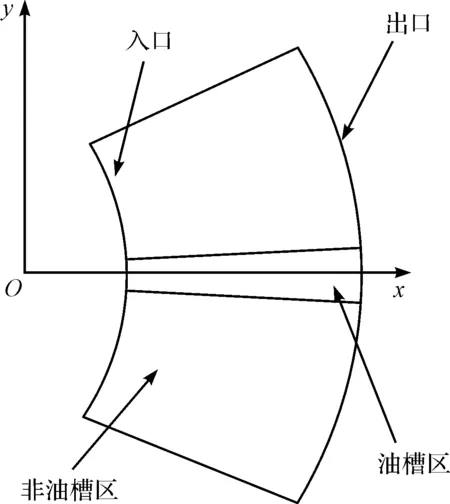
图4 油膜数值计算模型

图4中的入口代表油液流入的入口，出口代表油液流出的出口。

根据建立的模型，可将Navier-Stocks方程[17-18]简化为：

(4)

(5)

式中：Vx，Vy—油膜x和y方向的速度，m/s；P—油液压力，Pa；ρ—油液密度，kg/m3。

对式(4～5)分别积分两次，可得：

(6)

(7)

式中：Uix,Uiy(i=1,2)—摩擦片与对偶片转速在x和y方向的分量，rad/s(其中Δω=ω1-ω2)。

根据模型积分条件，可表示为：

z=0,Vx=U1x,Vy=U1y
z=h,Vx=U2x,Vy=U2y

(8)

公式(6～7)对h分别积分，可得流量沿x和y方向的流量方程：

(9)

(10)

其中，流量方程中包括3项：第一项为压力差流量；第二项为剪切流量；第三项为离心流量[19-20]。

油膜的连续性方程为：

(11)

由连续性方程(11)可得：

(12)

将Vx，Vy代入式(12)，并且对z进行积分可得：

(13)

该方程描述了摩擦片间油膜压力和膜厚之间的关系。由上式可得：等号右边的第3部分和第4部分反映的是离心力对油膜状态的影响，而dh/dt反映的是油膜的挤压效应产生的作用；当挤压速度与施加的外载荷方向相同时，油膜的厚度变小(dh/dt<0)，此时产生油膜承载力。

3.2 数值参数

本文选取功率为75 kW的液粘软起动装置进行分析，其摩擦片沟槽数为16，相关参数如表1所示。

表1 计算参数

3.3 仿真分析

笔者根据公式(13)，求解h关于t的关系。

利用MATLAB软件仿真分析可得起动过程中油膜厚度h变化，如图5所示。

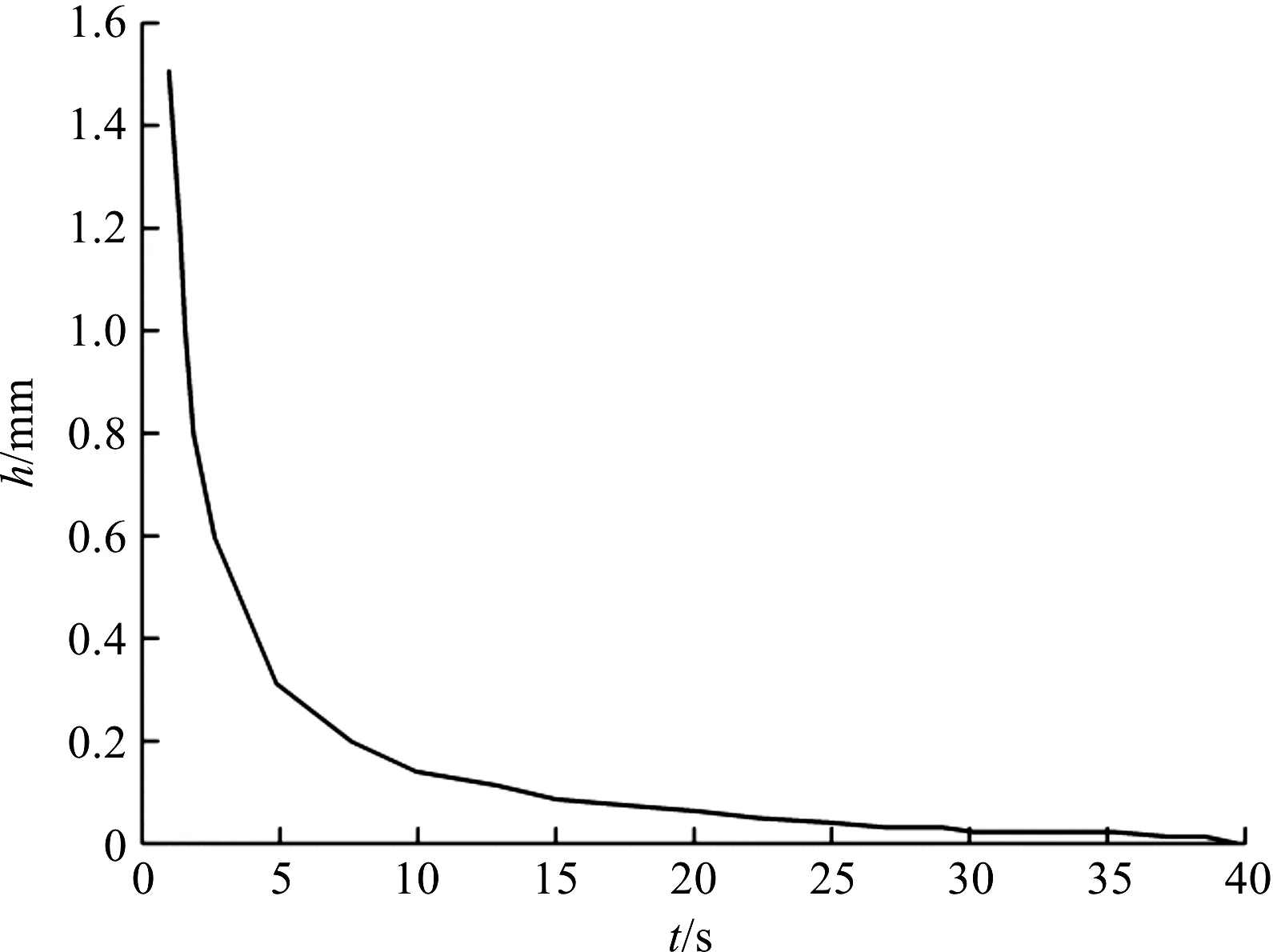
图5 起动过程中油膜厚度变化

由图5可知：起动过程中，油膜厚度随着时间的增加而逐渐减小，前10 s内油膜厚度变化很快，此时为流体润滑阶段；到40 s时油膜厚度几乎为0，此时为混合摩擦阶段，依靠油液和摩擦副之间的接触传递动力。

式(13)为液粘软起动装置起动过程中的瞬态雷诺方程，通过求解该方程可得油膜的压力特性，进而可得到油膜承载力及油膜传递转矩。

由计算可得其油膜的剪应力为：

(14)

(15)

式中：τx，τy—油膜在x和y方向上的剪切力，Pa(计算中应注意τx和τy的方向性)。

转矩M计算公式为：

(16)

油膜的承载力W为：

(17)

根据式(16～17)，利用MATLAB软件仿真可得起动过程中转矩及油膜的承载力的分布情况，如图6所示。

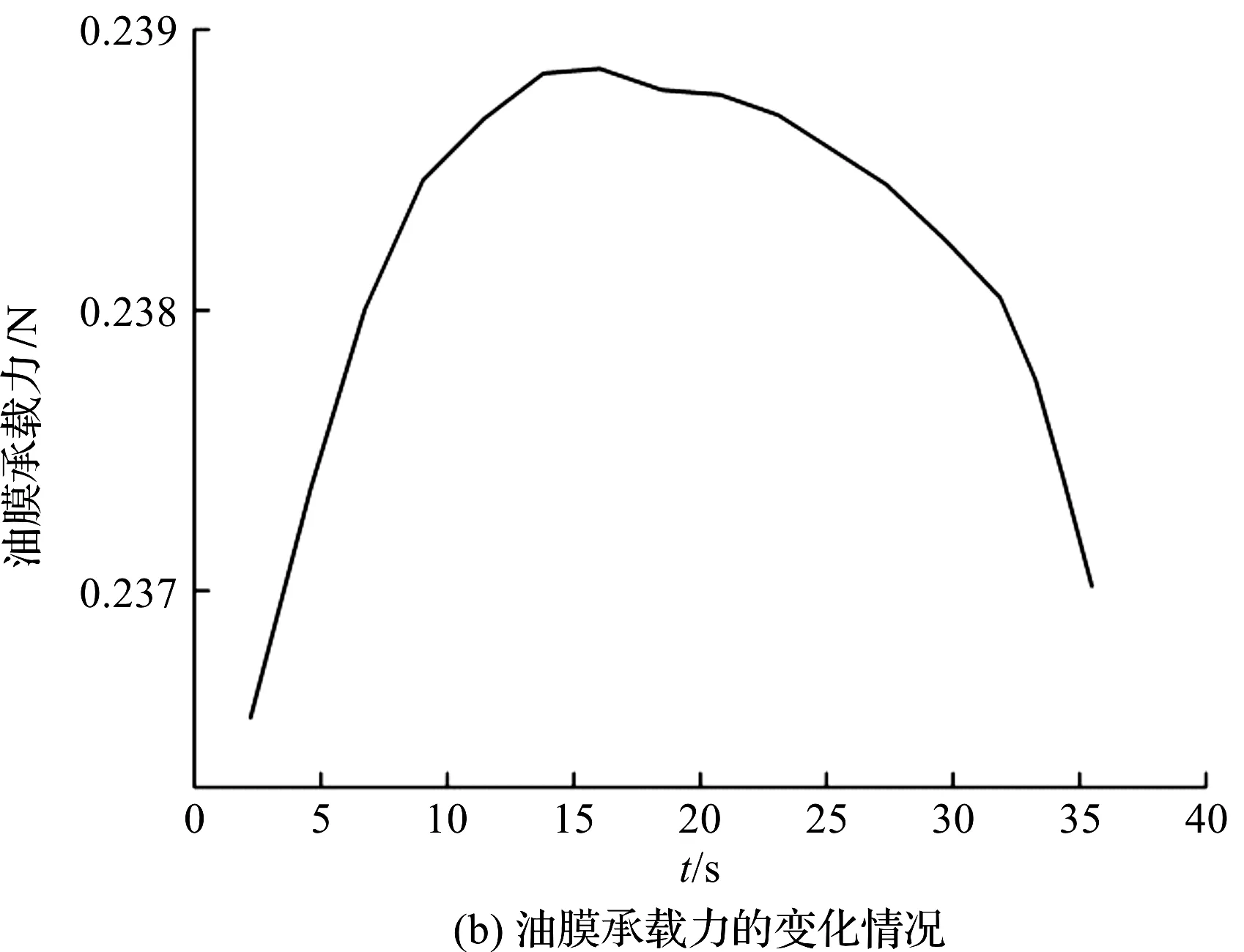
图6 起动过程中转矩和油膜承载力的变化情况

从图6中可以看出：起动过程中，油膜传递的转矩和动压承载力变化规律基本一致，随着时间的推移，扭矩和承载力逐渐增加，在起动16 s左右出现扭矩峰值和承载力峰值，而后逐渐减小。

4 结束语

本文主要介绍了液粘软起动装置的结构以及传递机理，分析了矿用带式输送机软起动过程中的速度曲线；采用液粘软起动的方式，对液粘软起动过程中的调速过程进行了分析，利用数值分析的方法得到了油膜的动态特性，主要结论如下：

(1)液粘软起动工作在调速过程中时，其油膜厚度随时间为动态变化，随起动时间的增加，油膜厚度逐渐降低，起动时间到达40 s时，油膜厚度为0，液粘软起动装置中的摩擦片与对偶片完全贴合，达到了同步传动；

(2)在起动过程中，由于油膜的动态变化，油膜产生的油膜承载力与扭矩将会发生相应的变化，其中扭矩和承载力随着起动时间的增加先增加后减小，当起动时间16 s时分别达到最大值，满足理想曲线的起动要求。

该研究可以为液粘软起动装置的设计与研究提供理论基础。