基于多岛遗传算法的薄壁齿圈装夹变形优化研究*

韩 军，段荣鑫，张 磊,王 静

(内蒙古科技大学 机械工程学院,内蒙古 包头 014010)

0 引 言

薄壁齿圈由于存在刚度低以及加工难度大的问题，导致其在加工过程中极易产生变形，影响加工精度。装夹变形是影响齿圈加工变形的重要因素，因此，减小齿圈在装夹时的变形对于加工精度的提高很重要。

针对工件装夹变形的研究，国内外学者在夹具类型、夹具布局、夹紧顺序等方面做了很多尝试和研究。秦国华等[1]通过BP神经网络对装夹变形有限元模型进行了预测，通过遗传算法对预测的模型进行了优化；许晓宇[2]提出了使用遗传算法对夹紧顺序、夹具布局和夹紧力同步优化的方法；陈蔚芳等[3]对FMS夹具进行了深入研究，对其中的专家系统的自动布局进行了探索；张传泰等[4]综合考虑了摩擦力、夹紧力切削力以及工件材料去除对工件装夹变形的影响，并基于有限元法和遗传算法，对夹具布局和夹紧力作了进一步的研究。

笔者研究的薄壁齿圈装夹变形问题，零件毛坯为环形，夹具布局根据夹具的个数采用均匀分布，夹具布局已经固定，因此直接对夹具结构和夹紧力进行优化；通过对薄壁齿圈装夹变形的有限元仿真分析，将结果与遗传算法进行数据联合，采用多岛遗传算法对夹具结构和夹紧力进行同步优化。

1 齿圈装夹方案的数学模型

对于齿圈毛坯的装夹变形研究，为了使得有限元软件仿真分析符合实际加工过程的装夹环境，本研究必须满足静力平衡条件、摩擦约束以及夹紧力约束条件。

1.1 静力平衡条件

在齿圈的装夹过程中，假定在工件周围有m个夹具元件，工件受到外力旋量We和夹具元件作用在表面的法向夹紧力Fin。

工件装夹时的受力图如图1所示。

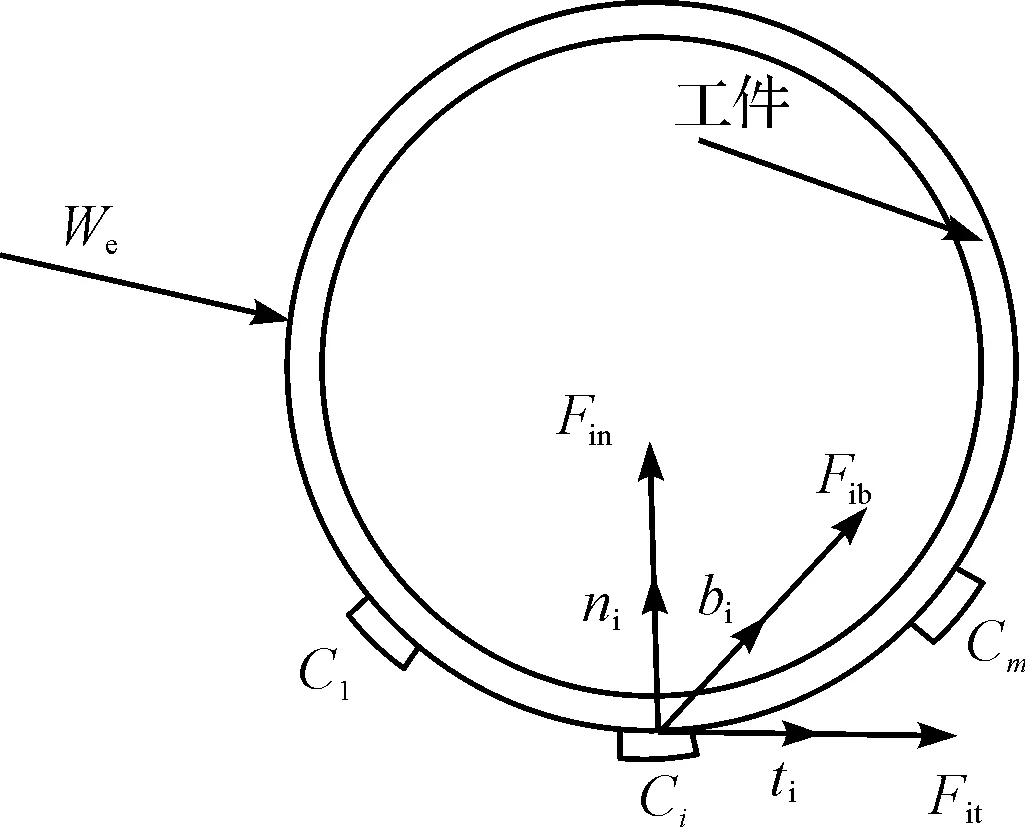
图1 装夹时工件受力图We—外力旋量(齿圈自身重力和加工时的切削力的合力)；ni,ti,bi—工件第i个夹紧元件接触位置处的单位内法矢量以及两个正交的单位切矢量,ni=[nix,niy,niz]T,ti=[tix,tiy,tiz]T,bi=[bix,biy,biz]T；ri—工件在第i个装夹元件处的接触位置，ri=[xi,yi,zi]T；Fi—在第i个接触点处的接触力，Fi=[Fin,Fit,Fib]T

装夹时工件应满足的静力平衡方程为：

We=KiFi

(1)

(2)

式中：Ki—夹具布局矩阵；Fi—夹具作用在工件上的载荷。

1.2 摩擦约束

作用在工件表面的切向力不能超过限制摩擦力，即：

Qi≤μFin

(3)

式中：Fin—第i个接触点处的法向力；Qi—第i个接触点出的切向力；μ—接触点处的静摩擦系数。

1.3 夹紧力约束

为了使工件定位准确，同时又能完全固定，工件必须始终与夹具元件保持接触，且夹紧力方向必须指向工件。因此，夹紧约束为夹紧力Fi与工件夹紧面外法线矢量的点乘必须大于等于0，即：

(4)

接触区域的法向力必须低于工件材料的屈服应力，即：

Fin≤σyAi

(5)

式中：Ai—齿圈与夹具的接触区域；σy—工件材料的屈服强度。

2 多岛遗传算法与优化方式

2.1 多岛遗传算法

遗传算法是具有鲁棒性的搜索算法，可以解决复杂的大尺度、多变量非线性反演问题[5]。一般遗传算法涉及5大基本要素：参数编码、初始种群的设定、适应度函数的设计、遗传操作的设计和控制参数的设定[6-9]。

遗传算法的基本流程如图2所示。

图2 遗传算法流程图

Isight中的多岛遗传算法是一种对并行遗传算法的改进算法，具有比一般遗传算法更好的计算效率及全局优化能力。同一般遗传算法相比，多岛遗传算法具有以下两个不同：

(1)在建立初代种群。对参数进行编码时，Isight中多岛遗传算法采用格雷编码[10]，格雷编码如下：

(6)

(2)岛/子种群。Isight中多岛遗传算法将子代种群分为多个岛，间隔一定的代数会进行岛间迁移，增加种群的多样性。

一般遗传算法对于探索空间的能力有限，极易收敛到局部最优解，导致早熟。多岛遗传算法通过将种群分为几个岛，在各个岛上分别进行遗传算法的计算，每个岛相当于一个“小生境”，再进行岛间迁移，大大增加了种群的多样性，防止了早熟。

2.2 优化方式

笔者研究的薄壁齿圈为环类零件，夹具个数和位置已经确定，无需考虑夹具个数和位置以及装夹顺序对装夹变形的影响。

笔者采用多岛遗传算法对夹具结构和夹紧力大小进行同步优化，将有限元分析结果与优化算法进行数据联合，其具体流程图如图3所示。

图3 优化流程图

图3中：

笔者首先对薄壁齿圈进行建模，在有限元软件ABAQUS中进行仿真分析，得出工件的受力变形；将ABAQUS与遗传算法在Isight软件中进行组件集成，ABAQUS中得到的工件变形量作为目标函数值，通过多岛遗传算法进行优化，反复迭代，直至达到设定的目标代数，得出工件变形最小时的夹具结构尺寸及夹紧力大小。

3 实例分析

笔者使用该方法对某特种车辆厂加工的行星齿轮减速器上的齿圈进行优化分析。该零件毛坯为环形，内径226 mm，外径260 mm，高79 mm，采用20Cr2Ni4A优质合金钢，密度为7 850 kg/m3，弹性模量E=226 GPa，泊松比μ=0.28。

传统装夹方式如图4所示。

图4 传统装夹方式

3.1 装夹建模及有限元分析

传统的装夹方式是采用圆柱形夹具，夹具与齿圈接触近似于点接触，造成了装夹过程中齿圈的受力集中，导致变形较大。

为改善装夹时的齿圈变形，笔者对夹具结构进行了改变，将夹具改为弧形，增大了与齿圈的接触面积，使得齿圈装夹受力均匀，减小了局部过大变形。

改善后的夹具结构如图5所示。

图5 夹具结构图

在有限元软件ABAQUS中，笔者根据式(1～5)建立模型分析，将齿圈毛坯设置为各向同性的弹性体。由于装夹元件刚度大，不考虑其变形，将装夹元件设置为离散刚体；在建立模型时，采用表面与表面接触模型，装夹元件与齿圈毛坯之间接触的切向行为采用罚摩擦公式，摩擦系数为0.2，模型采用C3D8I单元进行网格划分。

建立好的模型如图6所示。

图6 齿圈装夹模型图

3.2 优化参数设置

在该例中，由于装夹元件改为弧形，笔者通过角度a来控制弧形夹具的大小，高度以H表示。

装夹元件尺寸取值范围如表1所示。

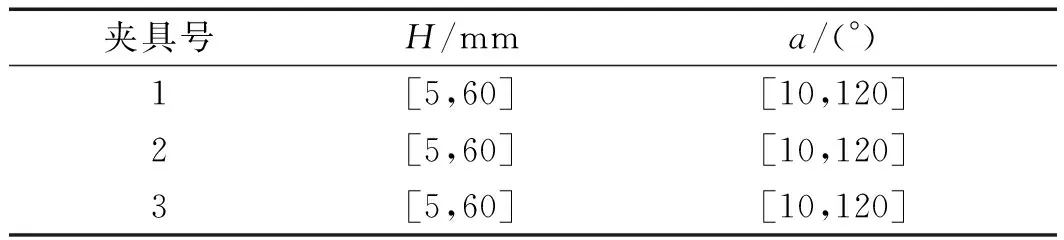
表1 装夹元件尺寸取值范围

由于将夹具元件设置为离散刚体，可通过参考点来控制夹具的运动，笔者直接在参考点上施加集中力来控制夹具。

夹紧力的取值范围如表2所示。

表2 夹紧力取值范围

对于多岛遗传算法的参数设置如表3所示。

表3 遗传算法参数设置

3.3 结果分析

笔者按照上述参数进行多岛遗传算法的参数设置，将遗传代数设定为300代。

优化过程中各变量变化过程如图7所示。

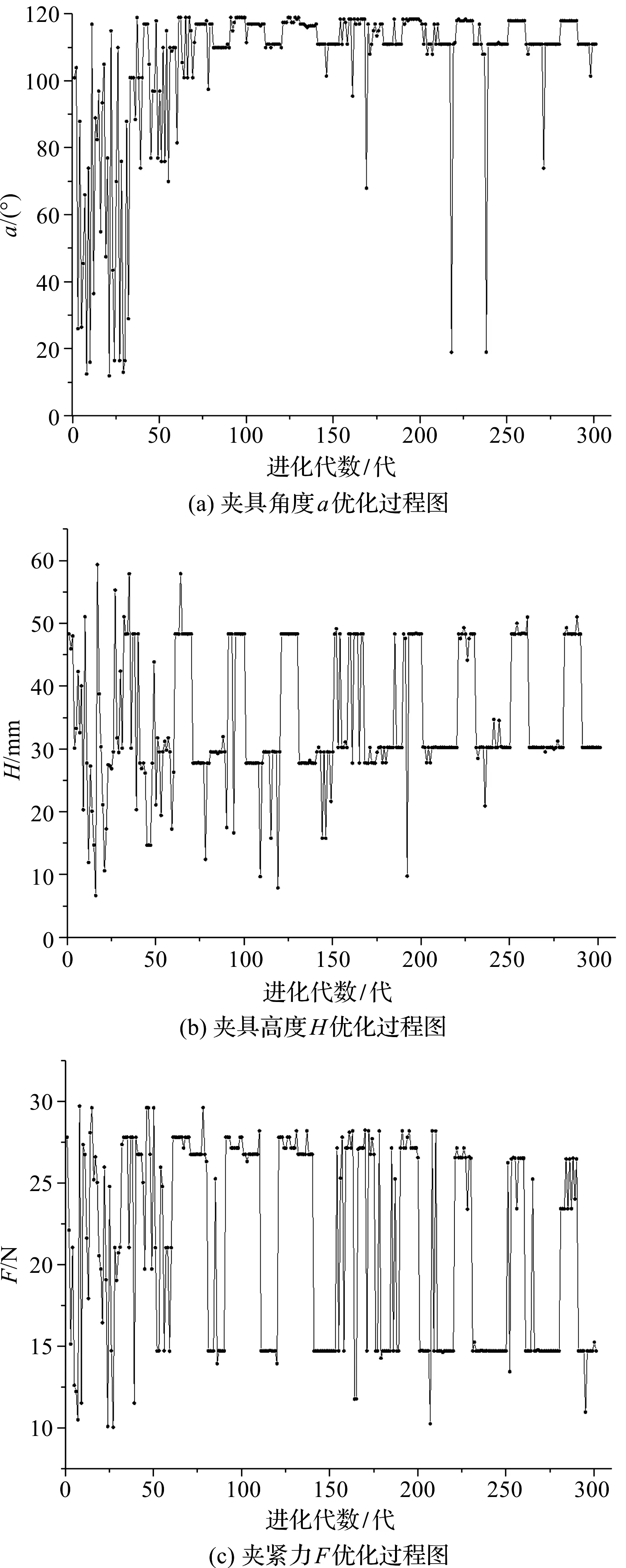
图7 变量优化过程

由图7可知：在变量的优化过程中，前100代变化比较大；100代以后，各变量取值多数趋于最优值附近，虽然有局部过大的变化，但是最终结果还是稳定在最优值附近，这是多岛遗传算法进行岛间迁移所致，这样大大增加了在优化过程中变量的种群多样性，也就是图中变量取值变化的原因，防止了陷入局部最优解的出现，但不影响最后的最优值的出现。

多岛遗传算法在进行300代计算以后停止，在优化过程中齿圈的最大变形量的变化，如图8所示。

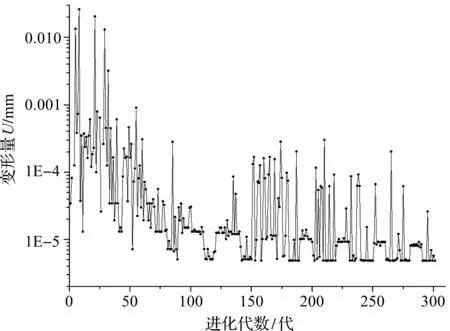
图8 装夹变形量优化过程图

由图8可知：在进行优化过程中，在100代以后，变形量逐渐平稳不变，后面虽然有局部跳动，但不影响优化的结果；优化到300代以后，结果趋于稳定。

笔者将改进优化后装夹元件进行有限元仿真分析，与原有的装夹方式及夹紧力下变形量进行对比，对比结果如图9所示。

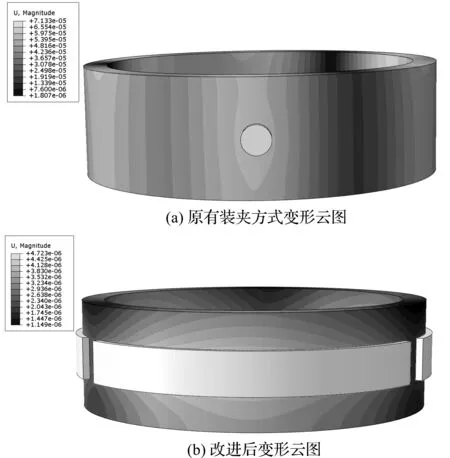
图9

由图9可知，优化后变形量显著减小。

优化前后夹具结构参数、夹紧力大小及变形量对比如表4所示。

表4 优化前后结果对比

由表4可知：通过夹具元件的结构参数和夹紧力的同步优化，得到薄壁齿圈装夹变形的最大变形量为0.004 723，而在传统经验设计夹具和施加的夹紧力装夹方式下，齿圈的最大变形量为0.071 33。由此可见，优化后变形量降低了93.38%。

本次优化不仅改善了夹具结构，同时施加的夹紧力大小有了准确的数值，不用靠人工经验来施加夹紧力；虽然优化前装夹变形就已经很小，但是经过优化后，变形量有了显著减小，对于后续齿圈的插齿加工精度有了很大的提升，验证了多岛遗传算法对于优化薄壁齿圈装夹变形的可行性。

4 结束语

以薄壁齿圈装夹过程的变形问题为研究背景，笔者通过遗传算法对夹具结构参数和夹紧力大小进行了同步优化，减小了因夹具结构参数和夹紧力的选取不当对装夹变形的影响；经对比验证结果可知，优化后的变形量明显减小。

笔者采用多岛遗传算法进行了优化，在各个岛上分别进行了遗传算法的计算，再进行了岛间迁移，将增大种群的多样性，大大减小了局部最优解的出现，能够有效地对装夹变形进行优化，有利于后续加工精度的提升。