基于级联失效的相互作用网络的动态分析

齐小彤 路立萍 隋缘 王思蒙 滕炜

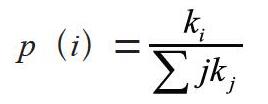
摘  要：相互作用网络是一种除了相互作用网络内部中节点间存在边外，网络之间还存在相互依赖的边。这种情况下，如果其中一个节点失效，由于该点存在依赖边指向另外一个网络，会导致依赖边所指向的节点失效，其称为级联失效，级联失效的存在会导致整个相互依赖系统的崩溃。文章针对级联失效所引起的整个相互依赖系统崩溃问题选取合适的优化模型，求出最大相互作用联通网络和最少的节点数量，最后根据实验过程对不同模型求解的优劣进行分析。

关键词：BA优化模型;hub节点;遗传算法优化模型

中图分类号：TP393.03      文献标识码：A 文章编号：2096-4706（2020）22-0161-03

Dynamic Analysis of Interaction Network Based on Cascading Failure

QI Xiaotong，LU Liping，SUI Yuan，WANG Simeng，TENG Wei

（Business School，Qingdao University of Technology，Qingdao  266520，China）

Abstract：Interaction network is a kind of interaction network，in which there are not only edges among nodes，but also interdependent edges among networks. In this case，if one of the nodes fails，because the dependent edge points to another network，it will lead to the failure of the node pointed by the dependent edge，which is called cascading failure. The existence of cascading failure will lead to the collapse of the whole interdependent system. In this paper，for the collapse of the whole interdependent system caused by cascading failure，we select the appropriate optimization model，find out the maximum interaction network and the minimum number of nodes. Finally，the advantages and disadvantages of different models are analyzed according to the experimental process.

Keywords：BA optimization model;hub node;genetic algorithm optimization model

0  引  言

相互作用网络被广泛运用到众多领域之中，其中有一种效应被称为级联失效，是一种一个节点失效，并且该点存在依赖边指向另外一个网络时，导致依赖边所指向的节点失效，从而放大了失效节点的后果。例如，2003年意大利和北美停电事故中，均存在电力-计算机网络构成了相互作用网络的问题。由此可见，相互作用网络与我们的生活息息相关，2010年，Sergey等人在Nature杂志上提出了相互作用网络的理论化模型和数学分析方法，引起了国内外学者的广泛关注。从那以后，相互作用网络模型被不断改进，从最初的一对一模型到多对多模型，从全局耦合模型到部分耦合模型，从一般的级联模型到负载级联模型等。目前，相互作用网络的研究主要集中在鲁棒性、级联控制与防御、攻击策略、级联模型的构建以及研究的数学方法的探索等。其中最为核心的问题是相互作用网络的鲁棒性研究。笔者结合学校的级联失效数学竞赛研究项目以及数学建模比赛参赛经验，对不同算法求解级联失效问题的效果做了进一步研究。

1  问题背景

近几年，相互作用网络受到国内外的广泛关注。级联失效的存在会导致整个相互依赖系统的崩溃。由于相互作用网络的特点，会导致一个节点的失效被放大进而导致整个相互依赖系统的崩溃，故其研究对于电力-计算机网络的结构发展创新起着重要作用[1]。

2  问题分析

2.1  问题一分析

问题一：建立合适的优化模型，对于选择的m个节点进行攻击，使得最终最大相互连通集团的节点数量g最少。并當m为1～50个时，对4个相互作用网络的g进行求解，利用MATLAB编程绘制出m与g的关系图。

经过查阅相关文献资料可知，本题中相互作用网络属于无标度网络mi，问题中对m个节点进行的攻击属于蓄意攻击，而蓄意攻击对于无标度网络而言，其鲁棒性更弱，会使网络迅速瓦解，崩溃的节点数骤增。经过硏究分析发现，发生崩溃的节点大部分为网络中的hub节点，即节点度数高的节点，其往往会对网络造成很大冲击，进而引起严重的级联失效。因此建立模型的目标是基于在无标度网络模型中找到hub节点，并对其进行攻击，可得出最大相互联通集团的节点数最少，对其进行进一步的分析，确定m与g的关系，绘制出相应的关系图。

2.2  问题二分析

问题二：对问题一中所选定的优化模型在基于实际操作的基础上进行展开分析，研究其时间和效率问题，并对操作过程中所发现的问题在题目中提示的启发式算法中选取更适合的模型。

问题二首先要求对问题一中的优化模型进行评价，经建立BA优化模型求解过程，可发现BA优化模型[2]实际应用过程中存在着耗费时间长，效率低下的问题。因此，面对BA优化模型所存在的问题，需要寻求更高效率的算法，经过文献资料和实际编程分析发现启发式算法相对于优化模型来说，效率更高。在对题目进行分析后，采用启发式算法中的遗传算法优化模型进行研究分析。

3  模型建立与求解

3.1  BA优化模型

3.1.1  模型建立

根据题目中要求和相应的文献资料查询可知BA无标度网络构造模型[3]如下：BA无标度网络构造模型是构建无标度网络的经典模型，其构造原理主要为增长和优先连接机制，其具体的构造方法为：（1）在起步阶段主要是进行网络节点的增长，开始时网络只有很少的节点（n0），每一时间步骤内增加1个节点，新增加的节点与已存在的节点有n（≤n0）条边。（2）其次在节点增长的基础之上，采用偏好连接的方式，使增加的节点以偏好概率p（i）与已经存在的节点i进行连接，满足的关系式为：

式中，ki为节点i的度数，j为所有已存在的节点。

建立BA优化模型，基于BA无标度网络构造模型中的构造方法中的（2）可知新节点连接原网络的方式，按照偏好概率往原网络中添加一定数量的新节点，然后对网络中添加的节点进行概率统计，统计后取出概率大的节点，以此概率作为节点的重要度评价指标。

3.1.2  模型求解

模型求解的具体过程为：（1）hub点的寻找：在选定好相互作用网络后，从其中选取m个相对重要的hub点，第一步首先将各个节点的度值求出，第二步基于构建的BA优化模型向原网络中增加一定数量新的节点，各个新节点的连接都以偏好概率p（i）与节点i进行相连，然后将各个新节点连接的原网络中的节点的编号进行概率统计，并将其中前m个概率大的编号进行保存，这也就是要寻找的hub点的位置编号。（2）蓄意攻击：本题的相互作用网络在蓄意攻击下有较大的脆弱性，也就是说明对hub节点进行攻击后经过级联失效[2]后，网络能得到相对较分散的相互连通集团，基于本题第一二问构建的main1_1函数，将相互作用网络的两个子网络A1和A2以及1中找到的hub节点的编号作为输入，对网络进行蓄意攻击。

3.1.3  模型结果

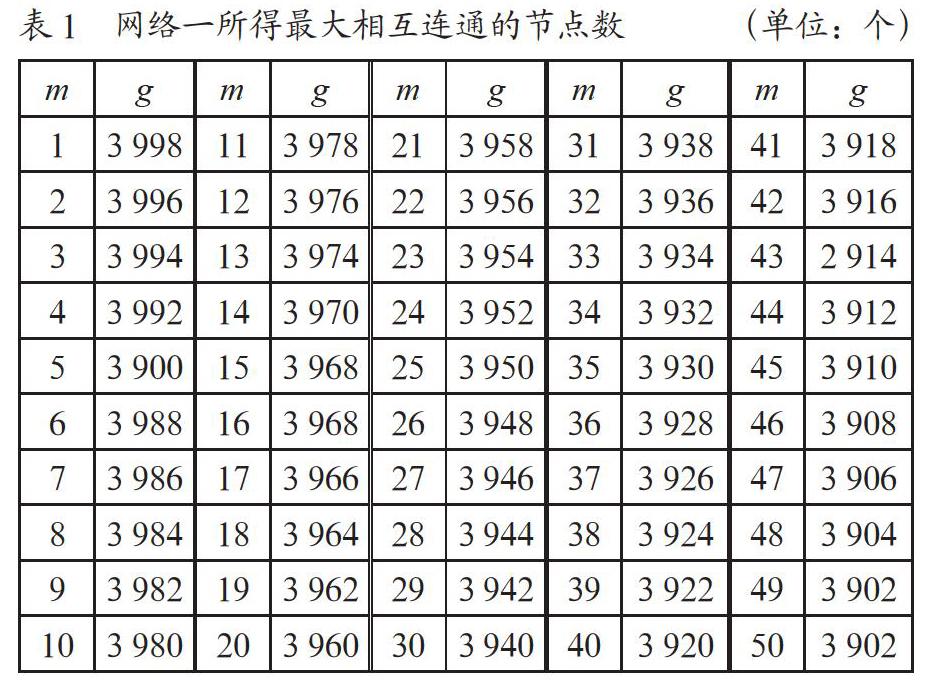
对已选好的网络进行hub点的寻找和蓄意攻击后，每次选取不同的m值，便可得出相对应的最大相互连通的节点数g。这里以表1中网络一的数据为例进行展示（m依次从1取到50，一共50个数）。

根据上述数据结合题目和实际操作分析，当网络中各个节点的偏好概率p（i）大致相同时，说明从中选取的节点相对别的节点的重要度变化不大，对选取的节点进行攻击后引起的级联失效不能产生明显的效果。

3.2  遗传算法优化模型

3.2.1  模型思路

为了对模型进行改进，查阅众多文献资料[3]，得知BA优化模型存在耗费时间长，效率较低的问题，选取遗传算法优化模型[4]作为所提及模型的改进。遗传算法（Genetic Algorithm，GA）是一种通过模仿生物界特有的繁殖和基因传递模式而产生的启发式算法[5]。其主要特点是直接对所确定的结构对象进行操作，不需要确定规则便可自动获取和指导优化搜索空间，其可以自适应地调整搜索方向。现在这一算法已经被广泛应用于相互作用网络的优化中，正是因为相互作用网络数据具有高复杂度，最终结果不明确等特征，才使得利用遗传算法这种非线性启发式算法来完成高复杂度的数据计算成为可能。

对BA优化网络确定节点重要度建立遗传优化算法，以各个节點的度值作为适应度函数，以m作为染色体的长度，染色体上所携带的数值为节点编号，其通过染色体的复制、交叉、变异等功能操作进行迭代，并将每次的最优节点的组合保存下来，最后在各代的组合中取出最优的组合，以此作为hub点。

3.2.2  模型建立

根据题目要求，建立启发式算法中遗传算法优化模型，其主要采用固定的交叉率、变异率和自定义的适应度函数，并且采用的是“轮盘赌”算法锁定最优解。因为模型只是对传统的遗传算法进行了针对本题的改进，所以不对模型的基础建立进行描述，只针对本题的遗传算法优化模型的主要参数进行说明：将节点数m作为染色体的长度、节点的度值ki作为适应度函数、每条染色体上所携带的信息为要攻击节点的编号，交叉率、变异率都是自定义数值，针对此问题取交叉率较小、变异率较大的情况，原因是当变异率较大时就会涵盖更多的节点。

将每次迭代后的结果进行对比可以得出适应度值较大的节点编号，以此作为相应的网络中相对重要的hub点。

3.2.3  模型求解

通过编写的MATLAB遗传优化算法的源程序main4_1，并将相互作用网络和m的数值等编写到b4_1脚本文件中，运行后可以得到四个网络的m和g的关系图，这里同样只展示如图1所示的网络一。

网络一图源程序代码为：

global num

num=0;   %最大相互连通集团的节点数初始化

load（'data1.mat'）; %载入数据

tic;

g=[];

for m=1：50                          %选择m个节点进行攻击

h1 = graph（A1）;          %h1为结构变量

h2 = graph（A2）;          %h2为结构变量

deg1= degree（h1）;      %将每个节点的度求出

deg2= degree（h2）;      %将每个节点的度求出

deg=[deg1;deg2];

%deg=deg1+deg2;

%提取度最大的节点

[x，da]=xlmax（deg，m）;    %取出m个最大值x为最大值向量，da为位置向量

% b=[];

% for e=1：2000

% b（e）=num;

%end

mian1_1（A1，A2，da）;       %对已经选出的节点进行攻击

g（m）=num;

end

subplot（2，1，1）

plot（1：m，g，'bo-'）;

xlabel（'m'）;

ylabel（'g'）;

title（'m和g关系图'）

legend（'网络一均值关系曲线'）

根据图1可知，网络一中的节点的偏好概率p（i）相对较平均，图像为一条直线，印证了表1的分析结果。

4  模型评价

4.1  模型优点

4.1.1  BA优化模型

根据题目要求及文献资料的查询，选定优化模型中的BA无标度网络构造模型，BA模型将复杂的网络的无标度特性，总结概括为增长和优先连接两个简洁明了的机制，便于进行研究和分析。BA模型开创性的把幂律度分布引入相互作用网络中，网络通过增添节点的方式在不断增长，并且新节点总是择优连接到高连通的节点上。经过实际操作可知，BA无标度网络构造模型以偏好概率连接，能够更加快速准确地找到所需的hub节点，其对于无标度网络的带有普遍意义的形成机理。

4.1.2  遗传算法优化模型

相对比于传统算法而言，遗传算法优化模型是从串集开始搜索，而不是从单个的解开始，其具有覆盖范围广、从全局角度进行择优的优势。遗传算法优化模型可以在更大的搜索区域内高效准确的获得相比于传统方法的最优解或者次优解，并且它所模拟的生物体的遗传和变异可以让问题求解的可控性和不可控性拥有更大的伸缩和操作空间，算法性能得到极大地提升。遗传算法优化模型主要是用概率机制进行迭代，具有一定的随机性，并且其扩展性比较强，容易和其他的算法进行结合。

4.2  模型缺点

4.2.1  BA优化模型

根据选取的BA优化模型，在实际操作过程中也存在一定的局限，在寻找hub节点的过程，其存在计算量大，效率较低，所耗费的时间较长的问题。

4.2.2  遗传算法优化模型

对于后期选取的遗传算法优化模型，其虽然有效解决了BA优化模型存在的时间和效率问题，但其本身也存在一定的缺点，遗传算法优化模型的编程比较复杂，对于参数的依赖性较大，并且算法的并行机制的潜在能力没有得到充分的利用。

5  结  论

本文首先介绍了级联失效问题的研究背景，进而对模型的建立以及模型的时间和效率进行分析，接着按照对两个问题的分析结果分别建立BA优化模型与遗传算法模型，并用两个模型分别对级联失效相互作用网络进行动态分析。根据结果可知，BA优化模型能更准确的找到所需的hub节点，但实际操作中效率较低，耗费时间较长;遺传算法优化模型扩展性较强，算法总体性能较优，但编程过程较为复杂，对参数的依赖度也较高。故在处理级联失效问题时，还要根据问题的实际情况选择适合的算法，才能更好地对问题进行求解。

参考文献：

[1] 李建春，吴雪丽，韩冰，等.一种对蓄意攻击具有鲁棒性的无标度网络 [J].河南大学学报（自然科学版），2013，43（3）：324-327.

[2] 陈志龙，郭平，谢嵩源，等.关联网络中的级联失效模型与分析 [J].后勤工程学院学报，2011，27（6）：87-91.

[3] 费凡.基于蛋白质相互作用网络的信息通路提取 [D].广州：华南理工大学，2017.

[4] 李庆，魏光村，高兰，等.用于求解TSP问题的遗传算法改进 [J].软件导刊，2020，19（3）：116-119.

[5] 曲志坚，张先伟，曹雁锋，等.基于自适应机制的遗传算法研究 [J].计算机应用研究，2015，32（11）：3222-3225+3229.

作者简介：齐小彤（1999.07—），女，汉族，山东潍坊人，本科在读，研究方向：国际商务。