一种改进的R-树节点分裂优化算法

摘  要：对R-树空间索引查询效率低下的问题，提出一种改进的PSR-树索引方法。PSR-树使用贪心算法找到要分裂的节点中对应的MBR的最小边界值，在最小边界值和非最小边界值中分别随机选择一个边界对象，用选择得到的这两个对象为分裂后两个新增节点首选空间数据对象进行分裂操作，建立好PSR-树后并写入节点。实验表明，PSR-树可以有效地减少节点中最小外接矩形的重叠面积，时间响应上比已有的R-树索引快，PSR-树从上述两个方面提高了查询效率。

关键词：R-树;最小外接矩形;节点分裂;最小边界值

中图分类号：TP391;TP301.6      文献标识码：A 文章编号：2096-4706（2020）22-0086-06

An Improved R-tree Node Splitting Optimization Algorithm

HE Jianying

（School of Intelligent Manufacturing，Sichuan University of Arts and Science，Dazhou  635000，China）

Abstract：To solve the problem of low efficiency of R-tree space index query，an improved PSR-tree index method is proposed. The PSR-tree uses a greedy algorithm to find the minimum boundary value of the corresponding MBR in the node to be split. A boundary object is randomly selected from the minimum boundary value and the non-minimum boundary value，use the selected two objects to perform the split operation for the two newly-added node preferred spatial data objects after splitting，and then write the node after the PSR-tree is established. The experiment shows that PSR-tree can effectively reduce the overlap area of the MBR in the node，and the time response is faster than the existing R-tree index，PSR-tree improves the query efficiency from these two aspects.

Keywords：R-tree;MBR;node splitting;minimum boundary value

0  引  言

在大数据、云计算等相关技术的推动下，空间数据、多维数据等词相继出现在人们的视野中，它们主要用来描述与位置有关的地理信息。但随着技术的不断进步，对非位置点数据也可以使用空间数据和多维数据等来描述。如对于学生基本信息表，其存储信息字段包括姓名、性别、年龄、出生日期、家庭住址、身份证号。这里可将该表视为6维空间中的点，每一维度分别对应某一属性。尽管各维的类型不尽相同，如姓名、家庭住址和身份证号是字符串类型，性别为比特型，年龄是数字类型，出生年月是日期型。其实对于家庭住址可以按定位的经纬度坐标，理解为空间位置。空间数据的存在则需建立与之对应的索引结构来方便空间数据的访问。

空间索引是提高空间数据访问性能的關键技术。目前的空间索引技术主要有基于二叉树、B-树、哈希以及空间填充曲线的索引等[1]。R-树就是B-树的一种扩展，在当前的空间数据索引领域中已得到了广泛的应用。R-树及其变体均是允许节点相互重叠的平衡树。R-树构建的好坏决定了访问R-树时效率的高低，而构建R-树的关键在于节点的插入与分裂。已有的研究表明R-树的构建实际上可以看成是一个聚类问题，可通过聚类算法及相应的分裂算法有效地降低R-树节点的重叠[2-4]。且在插入节点时，对子树的选择和节点的分裂等过程中，均是基于“使节点的最小外接矩形（Minimum Bounding Rectangle，MBR）的增量最小，则MBR的重叠区域最少”这一基本原则进行探讨研究的。

本文是在项目“大数据下R-树在高维数据去重中的应用研究”的研究成果之一，作者在文献[5]研究的“SR-树节点分裂优化算法”的基础上对R-树的搜索算法进行改进，提出一种改进的PSR-树空间索引方法，该方法的节点分裂优化算法是基于使R-树的MBR体积最小的原则，采用最小边界算法，找到MBR中的任意两个边界对象，以它们为分裂后的两个新节点的首选空间对象进行分裂节点的操作，最后把构建好的R-树存储在存储设备上。这样既增加了叶子节点的聚类性，又减少了叶节点的最小MBR的面积之和，从而提高了查询的性能。

1  相关工作

节点分裂是在构建R-树过程中，当插入数据对象的某一目标节点P已满，插入后节点数变M+1（M为节点所能容纳的最大节点数），此时数据集合将产生益出（overflow），那么需要对该节点P进行一分为二的操作，尽可能平均地把M+1个关键码分到两个子集中，并将某一中值关键码middleVlaue转交到父节点的pre_p中，对父节点pre_p使用同样的方法递归处理，直到没有节点需要分裂为止。若达到根节点也需要进行分裂操作，那么将增加一个根节点，树的高度增加一层。

R-树插入节点的过程大致为：查找到包含所需插入空间范围的MBR，找到将要插入数据对象所对应的节点，查看该节点是否已经包含了M个节点，如果是，则需要进行分裂操作。分裂后，两个MBR的面积之和要比原来的MBR的面积小。如果要插入节点的MBR有多个，则选择MBR最小的那个插入，如果没有最小的，那么遍历选择加入所需插入节点后MBR面积变化最小的那个MBR插入。

前人已经研究了针对R-树节点分裂的平方代价算法（Quadratic-Cost Algorithm）、穷举算法（Exhaustive Al-gorithm）、线性代价算法（Linear-Cost Algorithm）等[6]。Guttman平方代价算法在时间上从穷举法的O（2M）降低到了O（M2），时间复杂度有了较大的改进，但当数据对象较多时，平方代价算法执行分裂操作仍需要较长的时间，且不能保证分裂后的MBR的面积之和是最小的。而线性代价算法比较粗糙，虽然耗时少，但查询效率仍很低下。文献[5]在Guttman平方代价算法的启发下提出了SR-树节点分裂优化算法。其具体执行过程为：

（1）对需要分裂的节点随机选择两个种子R1和R2，保证R1，R2的MBR的空白面积都比其余的Ri大，分别以R1和R2作为新节点创建新的MBR。

（2）计算每次有Ri加入到两个新节点时，增加面积最小的那个节点，将Ri添加到该节点中，对每个Ri均递归调用此方法，直至把每个记录都添加到相应的节点集合中。

该算法在构建好R-树后，对其进行遍历查询时，减少了多路查询问题，同时在减少叶子节点的最小外接矩形的面积方面也取得了一定的成效。

2  空间数据索引设计

2.1  相关概念及定义

本节中直接给出R-树、空间数据距离函数、空间数据节点收益及最小边界等的相关概念。[7-10]

定义1：R-树是B-树的扩展，其包含两类节点：叶节点和非叶节点。设一棵度为m的R-树，其必定满足以下几点：

（1）除非叶节点是根结点，否则叶子结点中所包含的数据记录数在[m，2m];

（2）所有叶节点均处在同一层，是一棵结构平衡的树;

（3）根节点除外，其余的子节点包含[m，2m]个子节点;

定义2：设S类中的数据{s1，s2，…，sn}包含n个数据，则该类的第t个属性的均值点ct用属性的k个相关值描述可表示为：

定义3：设{s1，s2，…，sn}是n个d维上的空间数据集

合，设cj含有m个空间数据对象，则si与cj的距离函数为：

其中，i∈[1，n]，j∈[1，m]。

定义4：设{s1，s2，…，sm}是包含m个空间数据的集合，则该类的均值点c为：

其中，，d∈[1，m]，t∈[1，d]。

定义5：给定MBR矩形的长宽分别为w和h，设矩形的质量定义为Q（mr），s1节点所构成的最小外接矩形MBR的面積为mr1，删除某一数据后，矩形面积值为mr2，则该节点的收益为G（mr1，mr2），则Q（mr）和G（mr1，mr2）分别为：

定义6：设{s1，s2，…，sn}是空间数据集合，P是任意一数字，集合的P-边界值是空间数据集合的子集。即P? {s1，s2，…，sn}。

定义7：设{s1，s2，…，sn}是空间数据集合、任意一数字P及常量γ，设数据集合M的P-最小边界是由最小数量的对象组成的子集N。即满足：G（M，M-N）≥γ·G（M，M-P），其中γ∈[0，1]。

定义8：设{s1，s2，…，sn}数据集合的MBR边界MB，在空间数据集合中，层表示距离边界MB相等的数据对象的集合。

2.2  改进的R-树节点分裂优化PSR算法

根据第1节中描述节点分裂的原因和已有的分裂算法，结合MBR边界的思想。本文提出一种基于最小边界的节点分裂算法（P-border split R-tree，PSR）。其具体过程为：

算法1  PSR（leafnode， obj） /*PSR节点分裂算法*/

输入：等待插入的数据项obj，要插入的叶子节点leafnode;

输出：分裂后的叶节点;

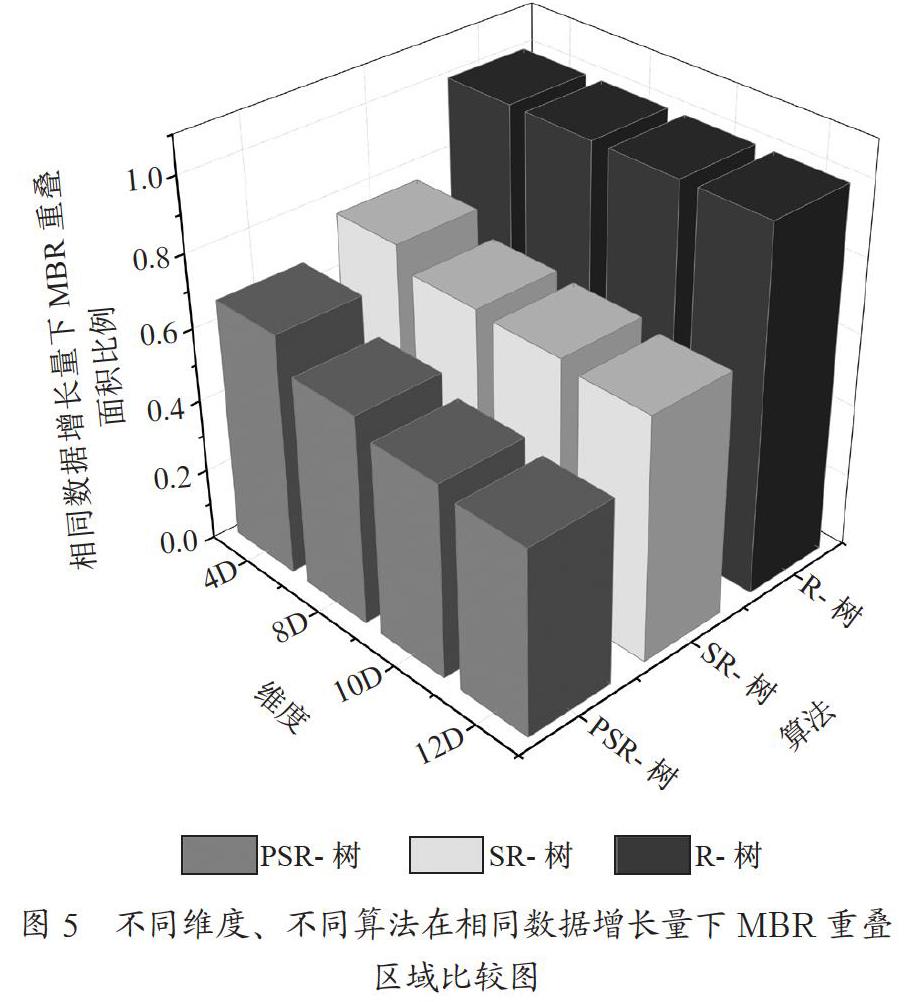
（1）  if（leafnode.length

（2）    leafnode.add（obj）;

（3）    return leafnode;

（4）  else p←p_border（s，p，m）;  /*此时对节点进行分裂操作，调用p_border（s，p，m）边界算法取出数据集合的最小边界值*/

（5）    p1_value=p.random（）;   /*从最小边界中随机取一个值*/

（6）    p2_value=p.random（s-p）; /*从非最小边界中随机取一个值存入p2_value*/

（7）    c1←?;

（8）    c2←?;

（9）   while pi_value ci  do {  /*i=1，2*/

（10）            /*求数据集合si中，与pj_value距离最小的数据项si，其中i∈[1，n]，j∈[1，M]*/

（11）    if d（si，pj_value）=min{d（sk，pj_value）}{ /*k∈[1，M]*/

（12）      leafnodei.add（si）;

（13）      wi←leafnode-leafnodei;

（14）      pi_value←ci;

（15）      pi_value←   /*重新计算质心并赋值给pi_value， i∈[1，2]*/

（16）    }end if

（17）   }

（18）   return leafnodei;

（19） }end if

在算法1中，首先判断叶节点所包含数据项的个数leafnode.length，如果leafnode.length小于节点能够容纳的最大数据项的个数，则直接把该数据项插入到该叶节点中。否则，leafnode.length大于等于叶节点能容纳的最大个数，则需要进行分裂操作，把一个叶节点分裂成两个叶节点返回，见行4到行16。分裂过程中，首先使用最小边界算法p_border（s，p），找到该叶节点的所有数据集合s中的P-边界最小值的集合，然后再随机找出两个不同的边界值分别存放在p1_value和p2_value中作为参照对象。再对剩下的数据项求使得d（si，pj_value）最小的数据项si，并将si划分到以pi_value为质心的集合中去，并重新计算新集合的质心，若两次的质心值相同，则认为已经使得集合最优，不需要进行集合的划分，此时循环结束。18行将返回分裂后的两个节点。两个节点划分的有优劣取决于最小边界值得选择，故在算法2中，使用贪心算法实现了P-最小边界值算法，其具体过程算法过程为：

算法2  p_border（D，p，m） /*P_最小边界值算法*/

输入：空间数据对象集合D，p及m的值;

输出：P-边界的值（集合）;

（1）   recive_D_struct（D）;  /*獲得D的结构*/

（2）   M←recive_ D _mbr（D） /*取D的MBR存入M*/

（3）   P←?;     /*初始化存放边界值得集合*/

（4）   flag=true;

（5）  while  （flag）  do{

（6）    gmax=0;        /*设收益的最大初值为0*/

（7）    MBmax=LEFT;  /*设置边界值的初始值*/

（8）    Layermax=0;

（9）    MB←receive_border（M）;    /*取得M中的每个边界值存放在集合MB中*/

（10）    while （MB） do{           /*遍历M中的每个边界值*/

（11）      for（i=1;i m;i++）{      /*遍历MB中边界对象的每一层*/

（12）     if（MB[j]）.layer[i]==0 && MB[j]）.layer[i].

size+|P|>p）   /*边界中包含i层上的数据对象，且i层上包含的对象与最小边界的和不大于输入的参数p时*/

（13）    border_split（MB[j].layer[i]）;  /*从边界中分裂第i层*/

（14）            /*d为i层上的对象数，每移除第i层上的数据对象时的平均收益*/

（15）          if  （g>gmax）  then{

（16）            gmax=g;

（17）            MBmax=MB[i];

（18）            Layermax=i;

（19）          }end if

（20）       }end for

（21）     }end while

（6）    if  （gmax==0） then{

（22）      flag=false;

（23）   }end if

（24）   p←border_split（MBmax，Layermax）;  /*从边界中分裂指定层的对象，把分裂后的集合存入p*/

（25）   MB←MB-p;   /*把分裂后的对象移除后，形成新的MBR矩形*/

（26）  }end while

（27） return P;

（28） }

在算法2中，对空间数据对象集合D及任意的p及m的值，使用贪心算法输出P-边界的值。行1到行4是初始化操作，行5到行26是对空间数据对象集合D组成的MBR矩形找到最小的边界值并放到集合P中。27行是返回P的集合作为P-最小边界值。

2.3  存储设计

通常建立的PSR-树会存于内存中，但随着大数据时代的到来，空间数据量也变得十分巨大，一旦存放于内存中的PSR-树消失，重新建立PSR-树要花费较长的时间。因此一般都会把建好的空间索引结构写入磁盘文件中进行存储。本文根据文件存储的相关特性，使用字节数组的方式对空间数据索引结构进行存储[6]。在PSR-树的文件存储中主要包含两类信息：树的信息和节点信息;叶节点中具体存放的是空间数据对象。可通过存储空间数据对象对于的ID标识。具体的存储过程为：

算法3  PSR_to_Storage_by_Byte（）

输入：树信息treeMess，树的根节点node;

输出：构建好的整棵PSR-树信息的字节数组;

（1）  B←new Byte（）;/*构建存放树信息的字节数组*/

（2）  size←write_Tree_Message_to_File（B， treeMess）; /*把树信息写入文件中，并返回树信息所占的字节数长度*/

（3）  BB←node_storage_to_Byte（node，size）{

（4）      tmepB←new Byte（）;   /*构建存放节点信息的字节数组*/

（5）     if node.level==0 then{  /*是叶节点*/

（6）       tempB.append（1）;

（7）     else  tempB.append（0）;

（8）     }end if

（9）     tempB.append（node.layer）;    /*添加节点的层次*/

（10）     tempB.append（node.targer.length）;    /*添加节点中所含实例项个数*/

（11）     data_list←recive_node_obj（node）;    /*获得node节点的索引项数据*/

（12）     foreach data_list do{           /*对node节点的索引项数据进行遍历*/

（13）      if（datalist[i].pointer==true） then {    /*该数据项有指向的子节点*/

（14）     otherB←node_storage_to_Byte（datalist[i]，size）;/*递归添加节点信息*/

（15）        tempB.append（size，otherB）;

（16）        size=size+otherB.length（）;

（17）      }else tempB.append（0）;{

（18）          tempB.append（node.ID）;

（19）      }end if

（20）   }end for

（21）  }

（22）  return B+BB

（23） }

该方法首先在内存中建立好索引树，然后在字节数组中先存入树的信息，包括树的高度、大小、空间数据维数、树节点能容纳的最大子节点数、最小子节点数、树信息存储后的节点偏移量等。然后把树的根节点作为第一个存入的节点，通過递归的方式把根节点下面的子节点依次存入字节数组中，直至叶子节点。

读取和访问树索引的过程较为简单，从文件头开始访问，根据根节点的偏移量找到根节点的位置，然后逐层访问。本过程采用字节数组的方式存储整个PSR-树，但对整个字节数组进行整体读写时，所花费发时间较长，且一次性地把整个字节数组读入内存，对内存的占有也较大。而对于一个高度为m的PSR-树，每次最多访问的节点个数为m，而不需要对整个树的节点一一进行访问。根据文献[6]可知，把每个节点的大小设置为一个磁盘存储页的大小，这样对节点的访问只需要一次读写操作就可以完成，有效提高了索引的效率。

3  实验及结果分析

索引算法的好坏，主要是看所构建的空间索引树中叶子节点的最小外接矩形的重叠面积的大小及查询时间消耗的多少来做判断：最小外接矩形的重叠面积越小，算法越优;查询所耗费的时间越短，算法越优。本文设计的实验有两个：一是比较不同的构建树的算法中最小外接矩形的重叠面积大小的比较;二是在不同算法中访问索引的时间消耗的对比。

本文所涉及的实验相关代码均使用Java语言实现，实验中所采用的数据集选取了文献[11]中所使用的Febrl数据集的数据生成器，人工生成了实验中所使用的实验数据。数据集中的信息包括姓名、性别、年龄、出生年月、家庭住址、身份证号、国籍等15项数据信息。在实验中，选取4维（4D）、8维（8D）、10维（10D）、12维（12D）4个不

同维度的各50万条数据，分别使用R-树、SR-树及PSR-树的算法建立空间结构索引树。在数据量从10到50万条，以10万条的数据递增时，数据所覆盖的区域面积也在增加，因数据集中的数据来源是随机的，故区域面积的增加不一定与数据量的增加成正比，其结果如图1到图4所示。

从图1到图4可以看出，当数据量成倍增长的情况下，MBR重叠面积区域并没有成倍的增长。在4维数据中，设置R-树算法下构建树产生的MBR重叠面积的参照值为1，SR-树所得到的MBR重叠面积是R-树MBR重叠面积的76%左右，而PSR-树的MBR重叠面积是SR-树重叠面积的87.6%，重叠面积小了近12.4%。随着维数和数据量的递增，MBR重疊面积增长的情况如图5所示。

从图5中可以看出，同等的数据增长量情况下，在4D到10D时，随着维度的提升，不同方法构建树的MBR重叠区域面积均明显下降，但当维数达到12D时，MBR重叠区域面积的变化不太明显，这是高维数据的稀疏性的原因，在建立MBR时已越来越紧凑。

对3种算法在不同查询区域中，对不同算法的响应时间进行比较。实验结果如图6所示。

从图6可以看出，PSR-树的时间响应在R-树和SR-树之间。这是因为虽然PSR-树的叶节点的聚集性强，减少了MBR重叠的面积，从而减少搜索的时间。但因在分裂过程中使用了贪心算法求最小边界值，此时其时间上有大量的消耗。故PSR-树的时间响应慢于SR-树，但仍然快于R-树的时间响应。

4  结  论

本文从R-树空间索引的构建到分析其查询效率低下的原因。在此基础上提出一种改进的R-树节点分裂优化算法：PSR-树索引。该算法在节点分裂过程中，通过使用贪心算法找到节点要分裂时其对应的最小外接矩形MBR的最小边界值，并在最小边界值中任意找到两个边界对象。以这两个对象为分裂后的两个新增节点的首选数据对象进行分裂操作。这样有效地增加了叶子节点内部空间数据的聚集性，从来减少了叶子节点最小外接矩形的面积。若将每次构建好的PSR-树存放在内存中，下次访问时需要耗费大量的时间进行PSR-树的重构，因此本文把构建好的PSR-树存到文件中，并使用递归的方式写入节点信息。实验结果表明，PSR-树比已有的SR-树和R-树在最小外接矩形的重叠面积上有明显的减少，而PSR-树中使用了贪心算法计算节点的最小边界值，故在时间的耗费上比SR-树要高，而比R-树的时间响应上仍有所提高。

参考文献：

[1] 陈菲，秦小麟.空间索引的研究 [J].计算机科学，2001，28（12）：59-62.

[2] 张明波，陆锋，申排伟，等.R树家族的演变和发展 [J].计算机学报，2005，28（3）：289-300.

[3] BRAKASTSOULAS S，PFOSER D，TTHEODORIDIS Y. Revisiting R-tree construction principles [C]//Proceedings of the 6th East European Conference on Advances in Databases and Information Systems.Springer-Verlag，2002：149-162.

[4] 孙殿柱，李心成，田中朝，等.基于动态空间索引结构的三角网格模型布尔运算 [J].计算机辅助设计与图形学学报，2009，21（9）：1232-1237.

[5] 徐明.基于节点分裂优化的R-树索引结构 [J].计算机应用研究，2016，33（12）：3530-3534.

[6] GUTTMAN A. R-Trees：A Dynamic Index Structure for Spatial Searching [J].Acm Sigmod Record，1984，14（2）：47-57.

[7] DU Q，GUNZBURGER M，JU L L，et al. Centroidal Voronoi Tessellation Algorithms for Image Compression，Segmentation，and Multichannel Restoration [J].Journal of Mathematical Imaging and Vision，2006，9（10）：177-194.

[8] PROIETTI G，FALOUTSOS C. Analysis of range queries and self-spatial join queries on real region datasets stored using an R-tree [J].IEEE Transactions on Knowledge and Data Engineering，2000，12（5）：751-762.

[9] 胡昱璞.动态k值聚类的R-树空间索引构建 [D].太原：太原理工大学，2016.

[10] 陈敏，王晶海.R*-树空间索引的优化研究 [J].计算机应用，2007（10）：2581-2583.

[11] DRAISBACH U，NAUMANN F，SZOTT S，et al. Adaptive windows for duplicate detection [C]//Proceedings of the 2012 IEEE 28th International Conference on Data Engineering.IEEE，2012：1073-1083.

作者简介：贺建英（1979—），女，汉族，四川金堂人，教师，副教授，硕士，主要研究方向：软件工程、机器学习。