稳定流态下海底管线局部冲刷有限元数值模型

陈海登，陶祥海，李 玲

(广东电网有限责任公司湛江供电局，广东 湛江 524005)

海底管线在海洋工程中得到了普遍应用。当管线铺设在沙质海床上时，管线的存在改变了周围的流场，增加了周围沉积物的输送速率，并直接导致管线周围的局部冲刷，从而引起海洋工程结构的破坏。目前许多工作致力于局部冲刷数值模型的开发，采用不同的湍流模型结合不同的经验输沙公式模拟冲刷进程，并用于预测管线下方的最大冲刷深度、管线上下游海床变化和漩涡脱落情况。Leeuwestein等[1]采用k-ε模型和推移质输移经验公式模拟海床变化，但是模型中没有考虑悬移质的输运，导致冲刷坑计算值偏大。van Beek等[2]基于k-ε湍流模型，建立了一个只考虑悬移质输运的冲刷模型，并将该模型用于预测管线下方的冲刷，预测的冲刷坑与试验结果吻合较好，但是下游冲刷变化有所偏差。Brørs[3]建立了一个既考虑密度影响又考虑悬移质和推移质输运的冲刷模型，利用该模型预测了清水冲刷，结果与Mao[4]的试验结果吻合较好，但是该模型没有模拟出管线后方周期性的漩涡脱落。Li等[5]采用大涡模拟方法建立了管线周围局部冲刷的数值模型，模型中假定河床剪切应力与清水冲刷下泥沙临界剪切应力相等，或直接采用动床冲刷下不受扰流的床面剪切应力，预测的最大冲刷深度和冲刷坑形状与试验数据吻合良好。该模型的主要优点是不需要任何泥沙输移公式，但是不能准确地预测冲刷过程。Liang等[6-7]建立了一个数值模型，用于预测清水和动床条件下管线周围局部冲刷的时间发展历程。该模型同时考虑了悬移质和推移质的输运，在曲线坐标系下采用有限差分法进行求解。在模型中使用了新的时间推进算法和沙滑模型，分别采用标准k-ε模型和大涡模拟计算了整个冲刷过程。结果表明，标准k-ε模型的计算结果比大涡模拟计算结果更加精确，冲刷剖面对流场的计算网格密度的依赖性较小。

本文通过有限元法[8]建立了一个冲刷数值模型，基于非定常雷诺平均N-S方程和标准k-ε湍流模型来模拟水流流动，采用经验公式来模拟推移质运动，利用动网格方法[9]来捕捉水沙交界面，所有方程采用特征线法[10]进行时间离散。通过高雷诺数下二维钝体绕流和Mao[4]的清水冲刷试验对模型的有效性进行验证。

1 数值模型

1.1 水流控制方程

流场求解采用非定常雷诺平均N-S方程，湍流模型选择k-ε模型，控制方程如下：

(1)

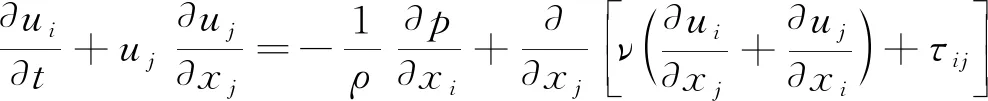
(2)

(3)

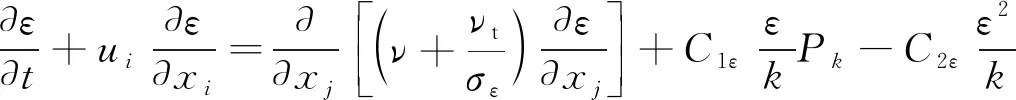
(4)

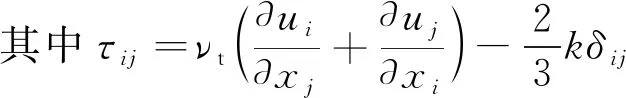
式中：ui、uj分别为在xi、xj(i=1,2,3;j=1,2,3)方向上的水流速度；ρ为水的密度；p为压力；t为时间；ν为动力黏度；τij为雷诺应力；k为湍动能；νt为湍流黏度，νt=Cμk2/ε；ε为湍动能耗散率；δij为克罗奈克函数(当i=j时，δij=1;当i≠j时，δij=0)；Cμ为经验常数，取值为0.09；Pk为由于平均速度梯度引起的湍动能的产生项；σk、σε、C1ε、C2ε均为经验常数，分别取值为1.0、1.3、1.44、1.92。

为了精确模拟冲刷，在求解过程中使用了动网格方法。动网格方法的基本思想是在每个时间步内，通过对流体区域的网格进行更新以实现由于边界运动引起的计算域与其物理量的变化，采用任意拉格朗日-欧拉(ALE)方法描述流体运动的控制方程，通过插值运算从旧网格映射得到网格更新后的各个物理量，然后对每个时间步内网格上的物理量进行迭代求解来获得流动的动态演化结果[11]。当前主要的动网格方法有虚拟结构法、偏微分方程法、代数法、网格重构法和网格变形与局部或全场网格重构结合[12]。本文通过构建方程，求解偏微分方程计算网格节点坐标变化。

采用动网格方法后， N-S方程中连续方程保持不变，仅需将动网格速度添加进动量方程、湍动能、湍动能耗散率方程中：

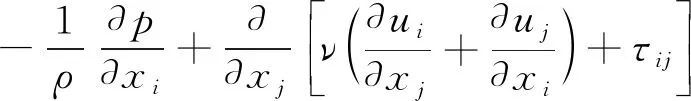
(5)

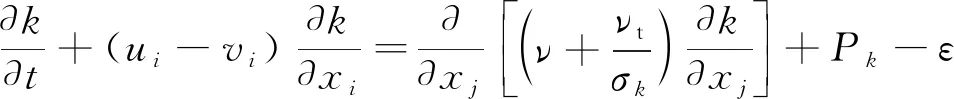
(6)

(7)

式中：vj为xj(j=1,2,3)方向上动网格速度。

1.2 冲刷模型

导致冲刷的主要原因是悬移质和推移质的运动[13]。悬移质输移模型适合用于挟沙运移，而不适用于只有沉积物形成的海床。本文只考虑推移质运移导致的冲刷。由于van Rijn推移质输沙率公式[14]中各参数意义明确，计算方便，易于理解，可以直接运用于河流、河口和海岸等地区，且本文分别采用有限元法和特征线法进行空间和时间离散，可以避免不稳定问题[15]，本文采用van Rijn公式计算推移质输沙率：

qb=ψub

(8)

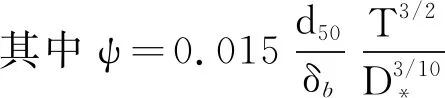
τωcr0=(ρs-ρ)gd50θcr

β=tan-1‖Hzb‖

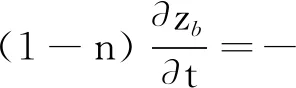
式中：qb为沿着海床单宽推移质通量；ψ为海床上的沉积物浓度；ub为平行于海床上推移质层面的水流流速；δb为推移质层的厚度，取δb=2d50；d50为颗粒的中值粒径；ρs为砂子的密度；T为海床面无量纲剪切力；τω和τωcr分别为海床面剪切力和临界剪切力，D*为无量纲粒径；g为当地重力加速度；τωcr0为平整床面临界剪切力；φ为颗粒的休止角；β为颗粒最大的滑动角；α为推移质层面流速ub与最大滑动坡度方向的夹角；θcr为水平面上的Shields常数，一般取0.048；H为水平梯度算子；zb为床面演变高度，采用Exner方程计算；n为海床的孔隙率。

1.3 离散方法

采用有限元法对该模型进行空间离散，特征线法对时间进行离散。一般地，任意守恒型方程可以写作如下形式：

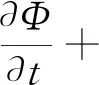
(9)

式中：Φ为未知量；F为对流通量；G为扩散通量；Q为源项。式(1)(5)(6)(7)都可写成式(9)形式。

除去三阶项，将式(9)沿特征线方向展开，采用张量记法的形式，m时刻的变化量为

ΔΦ=-Δt(·F+·G+Q)m+

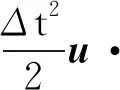
(10)

式中：Δt为时间步长；u为速度项；ΔΦ为未知量Φ变化量，同时，ΔΦ满足

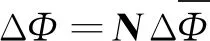
(11)

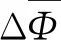
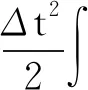
(12)

式中：Ω为计算域；n为界面外法线；Γ为积分域边界。

2 模型验证

2.1 雷诺平均的非线性k-ε湍流模型验证

采用笛卡尔坐标系下二维方形钝体绕流对雷诺平均的非线性k-ε模型进行验证，模型总长度为18H(H为方形钝体宽度)，高度为2H，方形钝体位于模型左端3H处，模型参数及边界情况见文献[16]。模型左侧为流体速度进口，右侧为自由出流，上下设置为滑移边界。将模拟结果与文献[16-18]结果进行了对比分析。设定雷诺数Re=40 000，与文献[17]中一致。

图1为钝体左侧0.2H处的水平速度和竖向速度分布与文献[16-18]结果的对比，其中u0为入口流速。由图1可知，计算结果与文献结果较为吻合，变化趋势一致，而且在近壁区域本文模拟结果更接近于实测结果，精度更高。

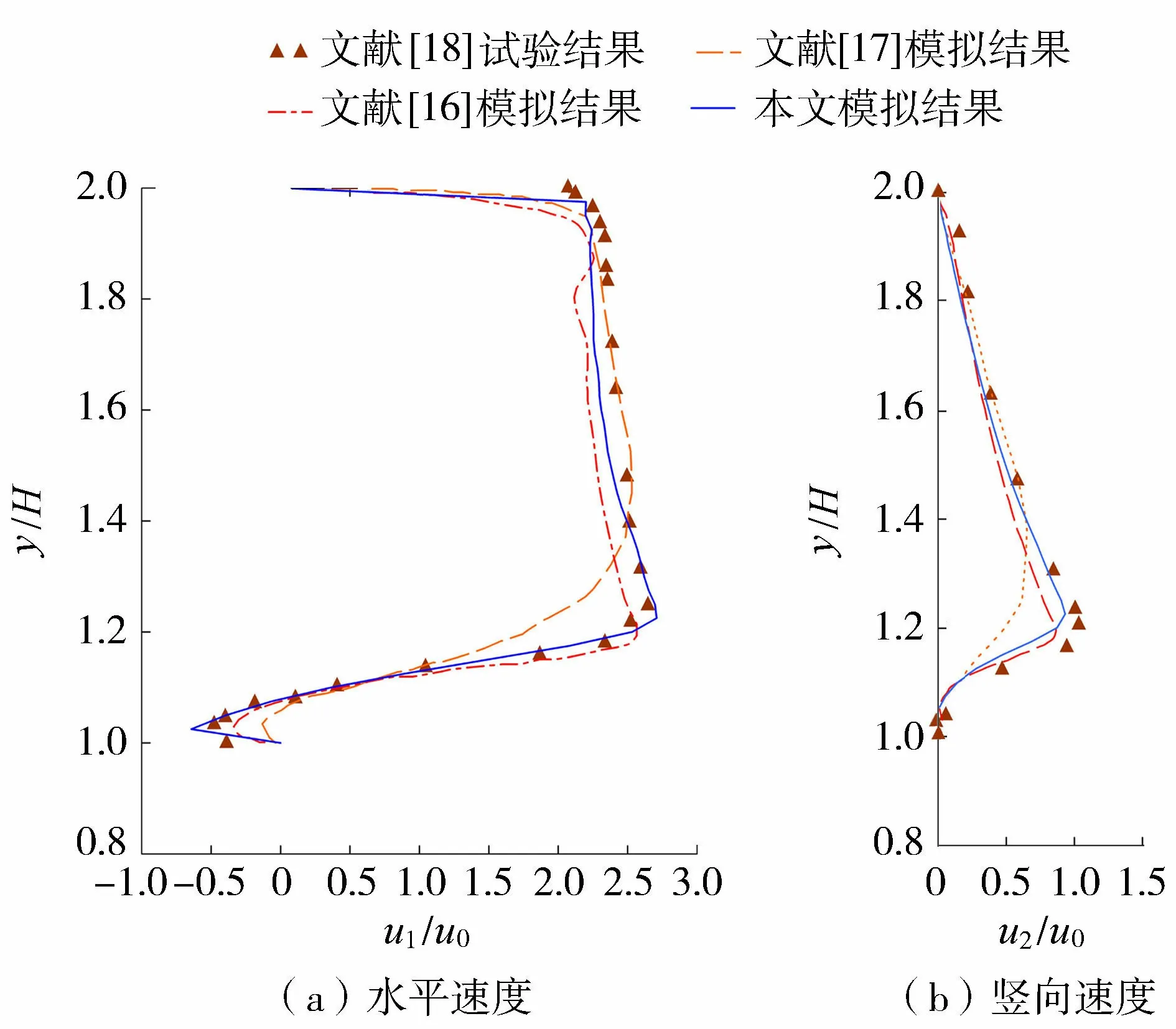
图1 速度分布对比

图2为计算得到的流线图，从图中可以看出，本文建立的模型可以捕捉到钝体背流面的主回流区、顶部的分离区、迎流面的小涡旋结构及背流面角点处的小涡旋。相比于文献[16]，本文模拟的流场可以更好地展现出背流面角点处的小涡旋，精度更高。本文计算出的主回流区长度介于钝体后方(1.0H～7.5H)范围内，与文献[18]的实测结果以及文献[16-17]的模拟结果相一致，表明本文计算方法具有较高的准确性，可以用于冲刷模型的验证。

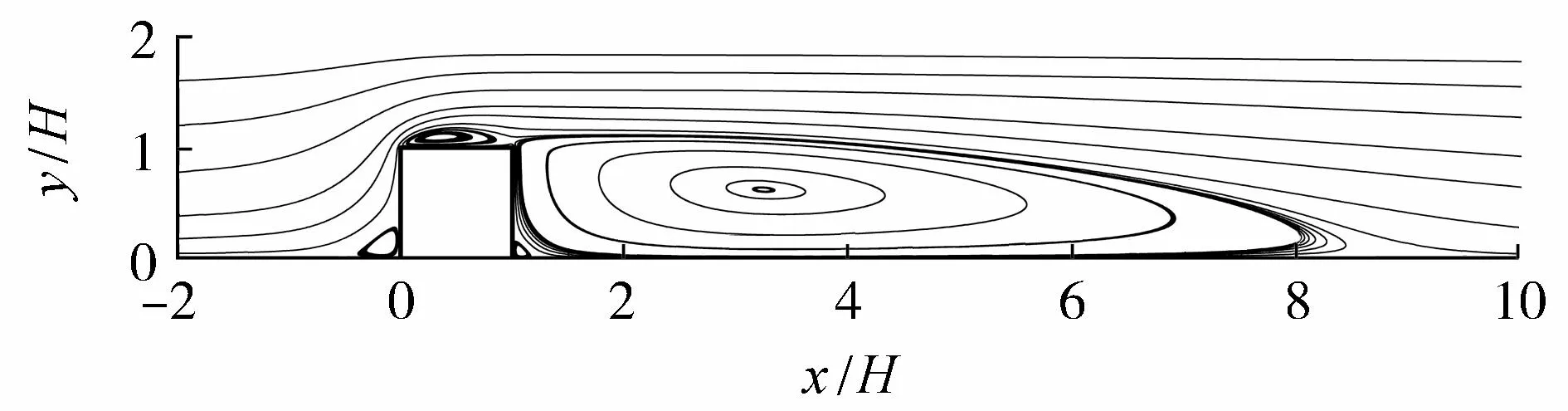
图2 流场结构

2.2 冲刷模型验证

为了验证模拟结果，采用Mao[4]的试验数据进行对比分析，其试验中管线冲刷条件为未扰动的希尔兹常数θ=0.048。在Mao[4]的试验中，管径D=100 mm，水深h=3.5D。海床表面颗粒的中值粒径d50=0.36 mm，进口水流速度为350 mm/s。

图3 网格划分

根据此试验，建立了二维有限元冲刷模型，上游计算长度为10D，下游计算长度为20D，水深为3.5D。为了避免在计算过程中网格拓扑结构的变化，在管线下方设置了一个初始冲刷坑，深度为0.1D，网格划分如图3所示。边界条件设置描述如下：① 进口(图3左侧)：y向速度设置为0，x向给定水平速度u1、湍动能k和耗散率ε，这些值是根据事先建立的一个相同水深，长度为100D的明渠模型计算获得，将此明渠的出口作为本模型的进口。②出口(图3右侧)：边界设置为自由出流，即速度、湍动能和耗散率的梯度为0，并给定压力参考点。③模型顶部设置为刚盖，即速度等变量在y向的梯度均为0。④在海床和管线表面采用了壁面函数[19]。

根据模拟结果，讨论在初始冲刷阶段(t≤30 min)的河床变化，并与Mao[4]的清水冲刷试验结果进行了对比。图4显示了不同时刻的冲刷形态。如图4(a)所示，开始阶段，由于管线上下游形成的压差，海床表面出现渗流。在渗流出口处，当压力超过泥沙的浮重时，冲刷开始发生。随着渗流的进一步发展，大量泥沙向下游冲去，沉积在管线后方，如图4(b)所示。经过一段时间后，管线和海床之间的间隙变大，并且泥沙在管线后方形成沙脊，如图4(c)所示。此过程持续，冲刷深度不断增加，沙脊也向下游移动，如图4(d)所示。

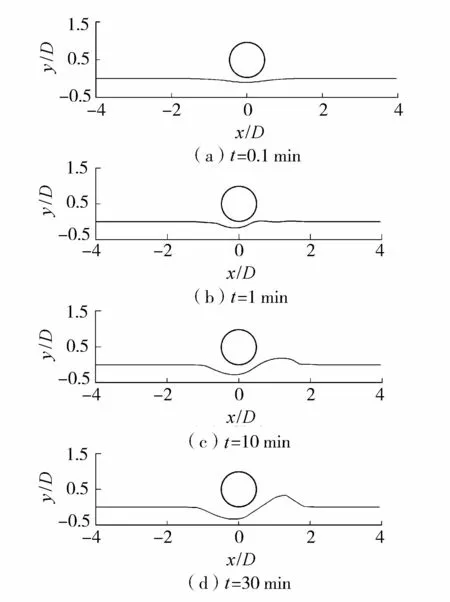
图4 不同时刻的海床冲刷形态

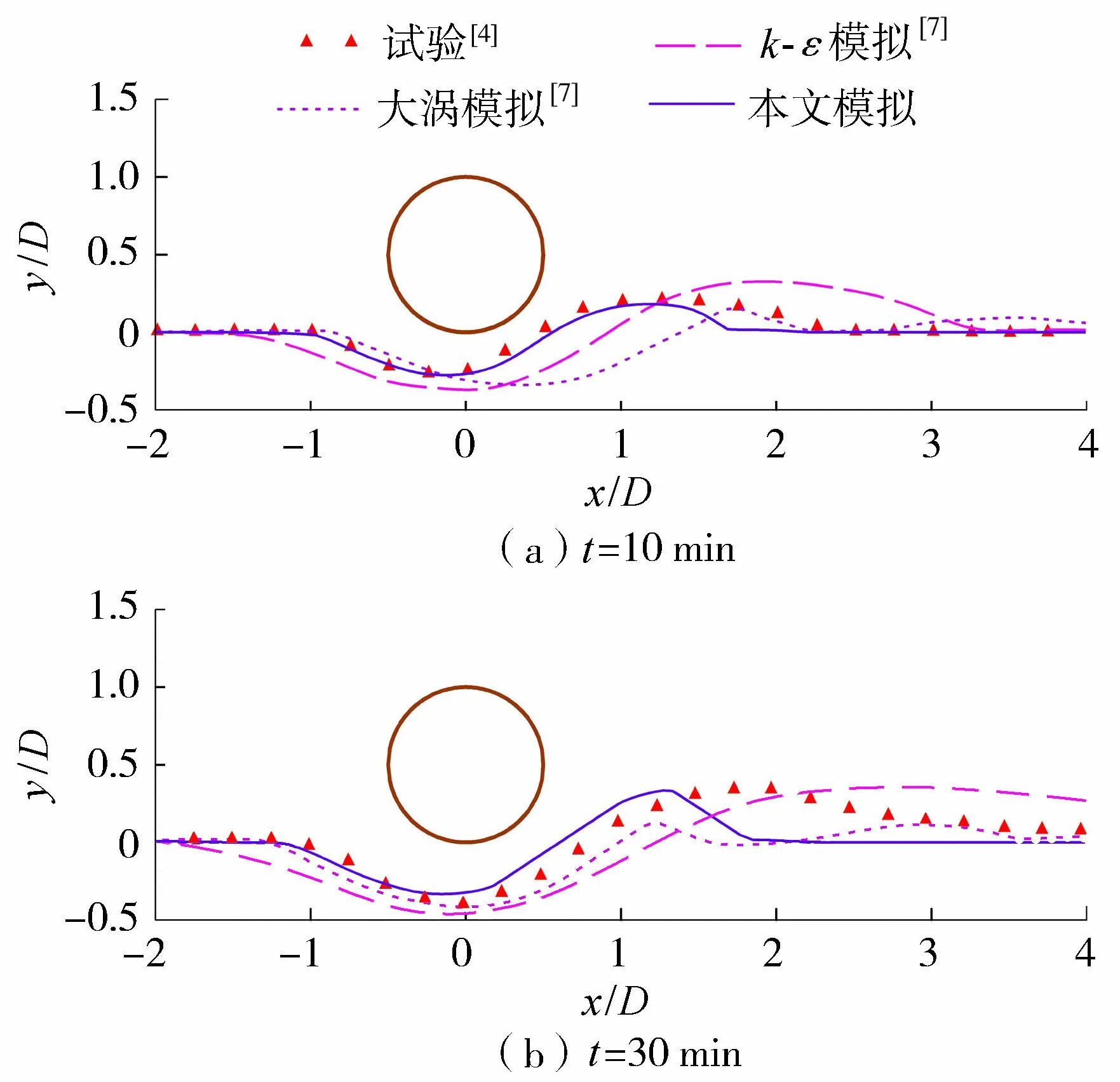
图5 不同时刻局部冲刷对比

图5为本文模拟结果与Mao[4]的试验数据和Liang等[7]的数值模拟结果的对比，可以得出：

a. 本文数值模型的计算结果与Mao[4]试验数据非常一致，尤其是在管线下方与沙脊之间，本文模拟的冲刷形态比Liang等[7]的k-ε模型和大涡模拟计算的结果更准确。

b. 从堆积形态上看，Liang 等[7]模拟的堆积高度高于Mao[4]的试验结果，而本文模拟值略低于试验结果，但更接近于试验结果。

c. 在沙脊后部，模拟的结果与试验相比有些不同，可能是由于未考虑泥沙休止角和忽略悬移质输运。如图5(a)所示，在冲刷初始阶段，模拟结果与试验结果吻合非常好，原因是此时的悬移质浓度很低，冲刷发生主要以海床推移质为主。随着时间的推移，悬移质的浓度开始增加，冲刷变成由悬移质和推移质共同作用，这就导致了模拟结果与试验结果有所差异(图5(b))。沙脊的模拟结果与Liang等[7]的大涡模拟结果相似，因为模型都没有考虑休止角，但是在起始阶段，Liang等[7]的大涡模拟高估了冲刷深度(图5(a))。

3 结 语

本文建立了一个有限元数值模型，用于预测海底管线在稳定水流下的局部冲刷。采用标准k-ε湍流封闭模型求解非定常雷诺平均N-S方程来模拟流场，采用有限元对模型进行空间离散，特征线法对时间进行离散。模拟的二维方形钝体绕流结果与文献[16-18]的结果吻合较好，验证了湍流模型的有效性。模拟的冲刷坑形状和冲刷深度与Mao[4]的试验结果吻合较好，在冲刷初始阶段的模拟结果更接近于试验值。与文献[7]的模拟结果相比，管线下方与沙脊之间的海床演变得到了更精确的模拟，但是沙脊形成后的模拟结果与试验结果有所差异，可能是由于模拟中未考虑休止角和悬移质的作用。

致谢：本文相关研究工作得到河海大学水利水电学院赵兰浩教授和广东省电力设计研究院李健华博士的帮助，特此致谢。