基于Maxwell-Stefan扩散模型的土壤碳通量计算方法研究
陈铭儒,胡军国,*,崔武峰,俞 平
(1.浙江农林大学 信息工程学院,浙江 杭州 311300; 2.中共杭州市临安区委统一战线工作部,浙江 杭州 311300)
土壤是生态环境中最大的碳库,其总储量约为1 394 Pg,每年向大气中排放的二氧化碳量在68~98 Pg[1];因此,土壤中二氧化碳浓度的细微变化都会对生态环境产生巨大的影响。研究土壤呼吸作用排放二氧化碳的变化规律对于缓解全球气候变暖具有关键作用[2]。在这一背景下,准确测量土壤呼吸排放的二氧化碳通量成为了生态学研究的一项重要课题。
目前,土壤呼吸碳通量的监测方法主要包括微气象法[3]和气室法[4]2大类:微气象法不能够测量小范围的碳通量,且仪器成本高昂;气室法成本较低、便于监测,广泛应用于土壤呼吸研究。气室法又可细分为动态气室法和静态气室法。其中,静态气室法利用碱液吸收二氧化碳而产生碳酸氢钠的原理,将密闭气室置于土壤上方,并在其内部放入氢氧化钠溶液,通过测定单位时间气室内部碳酸氢钠的产生量而计算出二氧化碳通量,此方法为最原始的二氧化碳通量监测方法[5-6],测量过程复杂缓慢,而且计算误差较大[7],现已不再使用。动态气室法的原理是利用高精度气体传感器来采集气室内部的二氧化碳浓度,通过得到单位时间内的积累量或气室内的流量差,从而计算出二氧化碳的通量值,是目前碳汇研究中使用最多的方法[8]。但动态气室法的缺点也较为明显:其一,气室在密闭期间会使二氧化碳在其内部堆积,从而抑制了土壤向大气中排放二氧化碳[9]:其二,弧形气室会干扰二氧化碳向上扩散时的湍流作用[10],因此会对扩散规律产生影响。这就使得动态气室法无法对二氧化碳扩散通量进行精确的测量。针对上述问题,本研究提出一种使用Maxwell-Stefan扩散模型,通过开放型气室计算土壤呼吸时排放二氧化碳通量的方式,旨在实现对土壤碳通量的长时间精确监测。
Maxwell-Stefan扩散模型由英国物理学家、数学家James Clerk Maxwell和奥地利物理学家Josef Stefan共同提出。在此模型提出之前,Fick扩散模型是计算流体通量最主要的方法,并已得到大量应用[11-13]。Maxwell-Stefan扩散模型在Fick扩散模型的基础上对扩散系数进行了改进和扩展,使之成为适用于计算多组分混合物扩散通量的数学模型。1962年,研究者Duncan和Toor在进行氮气、氢气和二氧化碳在2个储器介质之间扩散的实验时发现了氮气逆于浓度梯度进行扩散的现象[14],从而证明了多组分系统和二元扩散系统的扩散规律是不同的。在此之后,多项研究证实Maxwell-Stefan扩散模型在多组分扩散领域可以取得很好的计算效果[15-17]。使用该模型计算土壤呼吸碳通量主要有以下几点优势:第一,Maxwell-Stefan扩散模型的扩散系数使用矩阵来表示,矩阵中的元素反映了分子间作用力对其中2种组分扩散系数的影响,该模型能够很好地描述多组分扩散系统的状态;第二,该扩散模型非常适用于气相中的扩散过程,并在此领域已得到了广泛的使用,因此利用该模型来计算土壤呼吸碳通量更为适合;第三,Maxwell-Stefan扩散模型考虑到了分子的热力学运动,因此在对高温高压下的物质扩散进行计算时同样能够取得较好的计算结果。Moldrup等[18]运用Maxwell-Stefan扩散模型对土壤气体的扩散活动进行了仿真研究,并且取得了很好的效果,更加说明该方法适用于土壤碳通量研究。
本研究使用Maxwell-Stefan扩散模型计算土壤呼吸排放二氧化碳的通量,主要目的如下:其一,改进气室法存在的抑制土壤呼吸的问题,从而实现长时间的监测;其二,改进Fick扩散模型不能精确计算多组分扩散系统通量的问题,以此取得更高的二氧化碳扩散通量精度;其三,为基于开放气室的土壤呼吸监测装置研发提供理论基础。
1 材料与方法
1.1 半经验扩散系数
扩散系数是描述流体扩散能力的物理量,它表示某组分沿其扩散方向,在单位时间和单位浓度条件下,垂直通过单位面积的质量或物质的量。在Maxwell-Stefan扩散模型中,扩散矩阵由半经验扩散系数计算得到;因此,扩散系数是用于计算的关键因子。本文使用半经验法计算各组分扩散系数(D)。
(1)
式(1)中:T为热力学温度;P为大气压强;MA、MB为气体A、B的相对分子质量,本研究中二氧化碳气体的扩散介质为氮气,因此MA、MB分别取值MA=44、MB=28;VA、VB为气体A、B在正常沸点时的摩尔容积,VA、VB分别取值34.0和29.9。可以看出,D为关于温度和压强的函数。利用半经验扩散系数能够很好地描述二元组分之间的扩散规律,这也是流体力学领域中最为常用的扩散系数公式[18]。扩散系数与浓度梯度的乘积即为扩散通量。
1.2 Maxwell-Stefan扩散模型
Maxwell-Stefan扩散模型是适用于计算多组分混合物扩散通量的数学模型,是一种基于浓度梯度进行通量计算的方法。它在Fick扩散模型的基础上对扩散系数进行了改进和扩展,因此Fick模型是该模型在二元组分下的一种特殊形式。Maxwell-Stefan扩散模型将半经验扩散系数拓展为扩散系数矩阵,其中主对角线上的元素分别反映了物质的自扩散系数,主对角线以外的元素反映了多种物质间的相互影响[19]。Maxwell-Stefan扩散模型从分子之间的相互作用力出发进行推算。促使分子发生扩散的力被称为分子驱动力[20],由d表示,对于组分i:
(2)
式(2)中:μi为组分i的分子势能;xi为组分i的摩尔分数;R为气体常数,8.314 J·mol-1·K-1;grad表示梯度算子。
(3)
式(3)中:x为气体分子间距,μi可表示为
(4)
对于二元混合物而言,促使组分i和组分j分子发生相对运动的驱动力与2种分子的速度差和组分j的物质的量分数成正相关,可表示为
-dμi/dz=(RT/D)·[xj(ui-uj)]。
(5)
式(5)中:z为分子移动方向,ui、uj分别表示组分i、j的分子移动速度,D为二元组分系统下的半经验扩散系数。对于多元混合物,式(5)可拓展为
-dμi/dz=RT[xij(ui-uj)/Dij+xik(ui-uk)/Dik+…+xin(ui-un)/Din]。
(6)
更普遍的形式为
(7)
又有
Ni=ctxiui=Ji+xiNt,
(8)
式中,Ni为组分i的扩散通量,ct为混合物总浓度,Ji为组分i受分子作用力影响下的通量,Nt为混合物的总体扩散通量。整理可得:
(J)=ct[B]-1[Γ](x)。
(9)
式(9)即为多元混合物扩散的普遍化Maxwell-Stefan模型。其中:(J)为一维列矩阵,矩阵中每个元素为对应组分的扩散通量;[B]为扩散系数矩阵;Γ为热力学系数;x为各个组分的浓度梯度。式中:
(10)
(11)
式(11)中,δij为单位冲激函数,n为参与扩散的组分数量。
在本研究中,参与扩散的介质为氧气和二氧化碳,扩散介质为氮气和其他不参与扩散的气体组成的混合物,由于其他气体物质含量较低,对实验结果产生的影响可忽略不计,因此介质可以近似成氮气。根据上述方程,土壤呼吸过程的通量模型可表示为

(12)
式(12)中:D12表示二氧化碳和氧气之间的扩散系数,D13表示二氧化碳和氮气之间的扩散系数,D23表示氧气和氮气之间的扩散系数,x1为二氧化碳浓度,x2为氧气浓度。根据式(12),即可同时计算出每一时刻二氧化碳和氧气的通量值。
1.3 数据来源
本研究所使用的各种气体浓度数据由Ansys仿真系统进行仿真获得。Ansys为美国ANSYS公司开发的有限元分析软件,是国际上最受认可的计算机辅助设计软件,是一个非常适用于进行流体力学仿真的软件。本研究利用湍流模型,采用SIMPLE(Semi-Implicit Method for Pressure-Linked Equations)算法进行仿真数据的生成。其中,湍流模型用于根据设定的初始值生成不同高度的二氧化碳浓度和氧气浓度的时间序列,SIMPLE算法用于对产生的浓度进行压力修正。
二氧化碳和氧气的时间序列使用Spalart-Allmaras(S-A)湍流模型仿真生成。本研究拟对圆桶状气室进行仿真,S-A湍流模型适用于墙壁束缚流体运动,因此用其生成土壤呼吸的二氧化碳和氧气的时间序列是可行的。在Ansys-Fluent仿真系统中,需要为气体流速提供边界条件。气室壁面的边界条件由Fluent系统自动生成,不需要手动设定,因此只需要设定气室入口处,即气室底部的边界条件,包括入口速度、入口压力、入口浓度等边界条件参数。由于入口边界条件会在很大程度上影响到之后仿真时的扩散过程和最终生成的仿真数据;因此,在很多情况下,设定正确的入口边界条件都是十分重要的。本研究的边界条件均由实验采集而来。
仿真实验与真实的土壤环境存在的差异主要包括:第一,在实测条件下,不同气体的密度差异会导致扩散规律发生一定的改变。对于这一影响因素,Ansys仿真系统在进行初始化时会对各个组分的密度进行设定,生成的仿真数据都是将重力因素计算在内的。第二,受水平气流的影响,气流通过气室出口时可能会流入气室内部,从而干扰二氧化碳的扩散。为了尽可能地与真实的监测条件接近,对于这一问题,本文使用了S-A湍流模型。当气流流入气室内,会对内部气体造成低雷诺湍流运动,而S-A扩散模型最适用于低雷诺指数的湍流分析。实验将湍流强度设定为1%,接近于气流对于气室内部气体的影响。
本研究分别进行3组仿真实验,设定的二氧化碳通量分别是0.5、1.0、2.0 μmol·m-2·s-1,具体仿真参数见表1。
1.4 实现步骤
微生物和植物根部的呼吸作用会产生二氧化碳,土壤内部的二氧化碳浓度为0.15%~0.65%,远高于大气中0.039%的浓度,二氧化碳会随土壤孔隙到达地表,使得地表的二氧化碳浓度最高可达0.16%。土壤表面和大气之间形成的二氧化碳浓度差会导致二氧化碳由土壤表面向上方扩散,因此二氧化碳浓度会随高度的增加而降低,到达离地面约350 mm位置时与大气浓度持平。当土壤呼吸达到稳态时,二氧化碳会产生有规律的浓度梯度,采用线性拟合法就可以得到浓度梯度,此时便于使用Maxwell-Stefan扩散模型进行二氧化碳通量的计算。
仿真实验的建立步骤如下。
(1)建立气室模型。本研究所建立的圆筒状气室,直径200 mm,高度350 mm,气室底部与顶部均开口,其中底部紧贴土壤,二氧化碳由气室底部向顶部进行扩散。气室筒壁厚度为5 mm,气室顶部有3圈均匀分布的气孔用于与外界的大气进行气体交换,气孔的直径为5 mm,3圈通气孔距离气室横截面中心的距离分别为65、85、105 mm。建立好的气室模型如图1所示。之后将模型导入到Fluent程序中。
表1 仿真参数
Table 1 Simulation parameter

通量Flux/(μmol·m-2·s-1)速率Rate/(kg·m-2)T/KP/kPa入口CO2体积分数Inlet CO2 volumnfraction入口O2体积分数Inlet O2 volumnfraction出口CO2体积分数Outlet CO2 volumnfraction出口O2体积分数Outlet O2 volumnfraction 0.52.2×10-8298.51 0100.000 810.193 50.000 5960.209 81.04.4×10-8298.51 0100.001 070.193 50.000 5960.209 82.08.8×10-8298.51 0100.002 290.193 50.000 5960.209 8
(2)划分网格和建立控制方程。网格划分的精密程度决定了仿真实验的效果。网格的作用在于将气室这个整体分解成不同的区域,从而对每个区域分别进行浓度动态变化的推演。网格划分程度越高,所占用的计算机性能也就越多。Ansys仿真系统支持多种类型的网络。本研究采用三角形非结构化网格,其优点是生成网格的时间较少,适用于较为复杂的实体,并且对于未知方向的气流具有良好的计算性能,虽然计算数据的时间较长,但数据精确度高。实验中将气室划分成大约60万个网格。图2为气室网格划分示意图。
气室内部的气体属于典型的牛顿流体,通过牛顿的本构方程可以获得较为全面的流体力学方程组。在流场求解时所用到的动量方程可表示为

a,气室模型;b,气室半剖视图。a, Chamber model; b, Half section view of chamber.图1 气室结构图Fig.1 Structural diagram of gas chamber

a,气室壁面;b,气室底部。a, Chamber wall; b, Chamber bottom.图2 气室网格划分示意图Fig.2 Schematic chart of gas chamber mesh generation
(13)
式(13)中:φ为通用因变量,Sφ为广义源项,u为速度矢量,Гφ为广义扩散系数,ρ为密度,t为时间。
(3)边界条件设定。边界条件直接影响到生成数据的结果,因此应尽量接近大气环境值。组分气体采用二阶迎风格式进行离散,其他采用一阶迎风格式离散,气室避免采用无滑移条件。采用非定常计算,时间步长设定为0.1 s,满足Courant-Friedrich-Levy稳定准则。气室内部气体为近地表空气,主要成分为氧气、二氧化碳、氮气和其他气体,初始温度为298.5 K,考虑重力加速度与能量方程,土壤呼吸界面采用质量通量,湍流强度为1%,气室出口界面设定为自由流出。不同土壤所排出的组分气体含量不同,本研究采用的地表空气与土壤空气的各项组分气体含量如表1所示。由于其他气体组分复杂且含量较少,对本研究的影响可以忽略不计,因此其他气体均由水蒸气替代。
(4)由Fluent程序设定仿真初始化参数,并开始生成仿真数据,产生0~0.35 m处不同高度气体浓度的2 000 s时间序列。此时间段足够使二氧化碳的扩散在气室内形成稳态。
(5)根据设定的温度和压强计算Maxwell-Stefan扩散系数矩阵,并求得其逆矩阵。
(6)根据仿真系统生成的二氧化碳和氧气浓度时间序列,每隔10 s取一组0、0.10、0.20、0.30、0.35 m高度的浓度数据,从而获得200组二氧化碳和氧气的浓度数据。仿照获取的浓度数据,根据稳态情况选取相应的拟合方法计算出200组二氧化碳和氧气浓度关于高度的梯度值,并将每一组的二氧化碳和氧气浓度数据组成一个二阶矩阵。
(7)将扩散系数矩阵与每一组浓度梯度矩阵相乘,获得每一时刻二氧化碳的通量值。
2 结果与分析
2.1 二氧化碳浓度时间分析
在碳通量的监测过程中,二氧化碳浓度的变化规律是监测的一项重要指标,只有产生较为稳定的浓度梯度,才能够使用Maxwell-Stefan扩散模型进行碳通量的计算。因此,研究二氧化碳的动态变化,揭示两相混合气体在气室内的自由扩散机理,对提升土壤呼吸监测采样精度具有重大意义。图3为气室内部二氧化碳浓度变化。
从图3可以明显看出,整个气室内的二氧化碳浓度随时间延长而增加。在扩散过程中,大气表层与土壤气体由于缺少强对流作用,二氧化碳浓度的梯度变化较为平缓。经过一段时间的扩散,气室内的二氧化碳气体逐层上升,并在600 s之后趋于稳定。由此不难得出二氧化碳的扩散规律,首先是二氧化碳气体在气室内充分自由扩散的阶段,之后是二氧化碳达到饱和,进入平衡阶段。
仿真程序根据设定的通量值(0.5、1.0、2.0 μmol·m-2·s-1)分别进行二氧化碳的扩散仿真,并生成2 000 s内每一时刻不同高度的气体浓度值,其中二氧化碳的浓度值如图4所示。
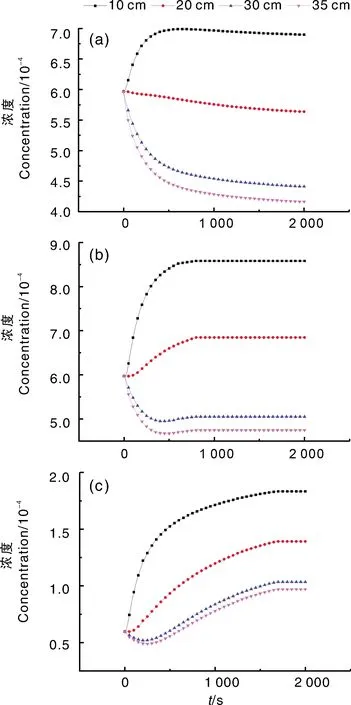
a~c中设定的通量值分别为0.5、1.0、2.0 μmol·m-2·s-1。下同。The set flux in a-c was 0.5, 1.0, 2.0 μmol·m-2·s-1, respectively. The same as below.图4 不同高度下CO2浓度的时间序列Fig.4 Carbon dioxide concentration of different altitude
由图4可知,气室内部二氧化碳的浓度随时间延长而增加,最后形成稳态,即气室内部各个高度的二氧化碳浓度不再随时间而显著变化。造成这一现象的原因是,开始时气室内部的二氧化碳浓度相比气室入口处少,二氧化碳由高浓度向低浓度扩散,而随着气室上方的二氧化碳浓度增加,下方浓度与上方浓度无法再形成能够产生扩散的浓度差,此时扩散运动就趋于稳定。当设定的二氧化碳通量值较低时,气室上方的二氧化碳浓度会呈现先下降后上升的趋势。这是因为二氧化碳气体的密度相对空气较大,而此时底部的二氧化碳浓度还未升高,因此二氧化碳不足以扩散到足够的高度。当扩散达到稳态时,气室内部的二氧化碳分布较为均衡,因此这一现象并不会影响到最终的计算结果。开放型扩散气室的设计能够使高浓度处的二氧化碳以垂直方向向低浓度处扩散而不受水平气流的影响,从而使二氧化碳的浓度变化规律更加明显,这样更易于使用Maxwell-Stefan扩散模型进行计算。另外,这样的气室还能够有效地减少气室对土壤呼吸的抑制作用。若使用封闭型气室,二氧化碳会在气室内部积累,一段时间过后气室内部各个高度的二氧化碳浓度将会相等,并且会随时间延长而不断增加,直至与地表的二氧化碳浓度一致从而不再发生扩散现象。从图4的数据可以看出,各个高度的二氧化碳浓度都有不同的变化曲线,并没有趋于一致,这也证明了开放型气室设计的优势。其中,0.5 μmol·m-2·s-1的扩散通量下,二氧化碳浓度在600 s之后达到稳态;在1.0 μmol·m-2·s-1的扩散通量下,二氧化碳浓度在800 s之后达到稳态;在2.0 μmol·m-2·s-1的扩散通量下,二氧化碳浓度在1 620 s之后达到稳态。气室内达到稳态的时间随通量的增加而延长,而在浓度达到稳态之前,浓度梯度逐渐减小,达到稳态之后浓度与高度成线性关系,因此稳态时浓度梯度的计算可以采用线性拟合法。这种线性关系也证明了在土壤呼吸系统中,使用Maxwell-Stefan扩散模型计算二氧化碳扩散通量是可行的。
2.2 Maxwell-Stefan模型计算结果分析
根据获得的200组间隔为10 s的数据,取每一组中0.10、0.20、0.30、0.35 m高度的浓度数据进行拟合,得出浓度梯度,并用Maxwell-Stefan扩散模型进行计算,得出2 000 s时间段内的通量值,计算所得通量值的变化曲线见图5。
图5显示了由Maxwell-Stefan扩散模型计算得到的二氧化碳通量值时间序列。初始时气室内部的二氧化碳浓度值与大气相等,而气室入口处的二氧化碳浓度较高,导致浓度梯度大,此时计算的通量值要高于实际设定的通量值,而随时间延长,通量值逐渐减小,最终趋于稳定,至稳态时,设定的0.5、1.0、2.0 μmol·m-2·s-1的通量下,计算结果分别为0.547、0.969、2.122 μmol·m-2·s-1,实验结果与设定值的误差分别为9.4%、6.9%、6.1%。可以看出,计算的精确度随设定通量值的提高而升高,产生这一现象的原因主要有2点:第一,二氧化碳扩散通量较低时,重力对扩散的影响较大,向上扩散的速度无法抵消重力的影响,导致一部分二氧化碳无法向上排放从而在气室底部积累,使气室下方的浓度梯度增大,扩散模型所计算出的通量结果也因此增加。第二,较小的扩散通量使得组分之间的相互影响力减小,而Mawell-Stefan模型的计算效果在组分的影响因素更多时才会更加明显。但要说明的是,以上这2点并不会对扩散模型的计算结果产生较大的影响,实验结果也证明,利用Maxwell-Stefan扩散模型计算的土壤呼吸时排放二氧化碳的通量与设定通量值非常相近。
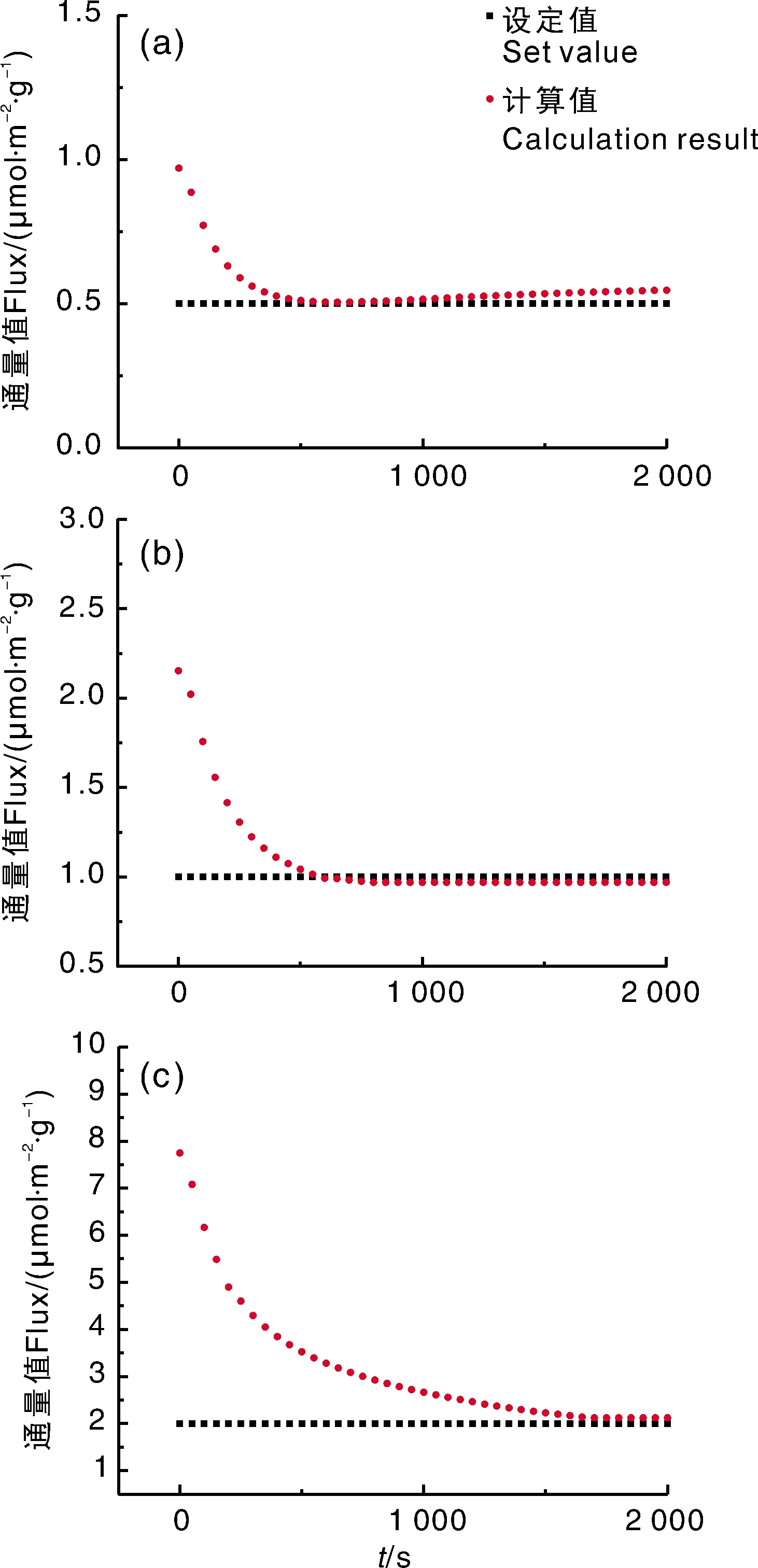
图5 Maxwell-Stefan通量值与设定通量值对比Fig.5 Comparison of calculated flux by Maxwell-Stefan with set flux
2.3 Maxwell-Stefan与Fick扩散模型计算结果对比
Maxwell-Stefan扩散模型是Fick模型的普遍情况,将Maxwell-Stefan模型计算得到的碳通量结果与Fick模型的计算结果进行对比,以便说明本研究中算法的合理性和优势所在。每隔10 s取一组二氧化碳浓度值,构成一个由200组浓度构成的时间序列,并对二氧化碳浓度进行拟合,得到二氧化碳梯度的时间序列,之后运用Fick模型进行二氧化碳通量的计算,其计算结果与Maxwell-Stefan模型结果的对比情况如图6所示。在稳态条件下,Fick扩散模型所计算的二氧化碳通量分别为0.589、1.044、2.286 μmol·m-2·s-1。可以看出,在多组实验下,本文算法所得的计算结果都小于Fick模型所得结果,且更接近设定值。当二氧化碳向气室上方扩散时,分子间的作用力会减缓这一过程,这会使扩散的通量值有所降低。Maxwell-Stefan扩散系数矩阵对分子间的这一影响因子进行了校正,在计算时减去了被减缓的通量。因此,利用这一模型所计算出的通量值为消除分子间作用之后的通量值。而Fick扩散模型将除二氧化碳之外的气体归于一种组分,不能够准确表述多组分之间的相互影响和扩散过程,这就导致了在计算多组分扩散系统的通量时Fick模型的效果不如Maxwell-Stefan模型,并且计算结果偏大。本文3组实验的结果很好地证明了这一点。显然,Maxwell-Stefan扩散模型从理论上能够更精确地计算土壤呼吸时排放二氧化碳的通量。
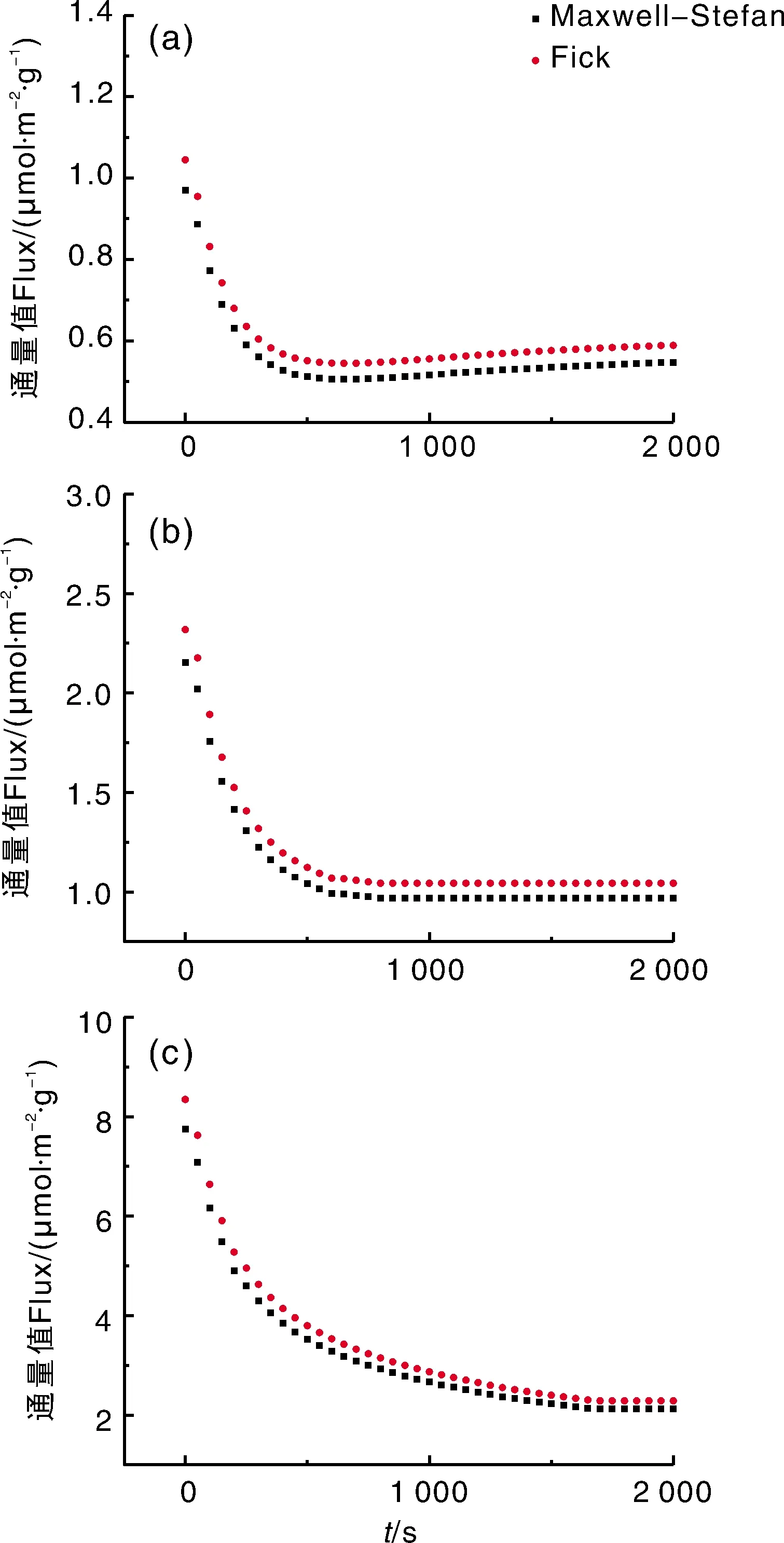
图6 Maxwell-Stefan模型与Fick模型的结果对比Fig.6 Comparison of flux result calculated by Maxwell-Stefan model and Fick model
3 讨论
Maxwell-Stefan扩散模型很好地解决了计算多组分扩散系统中扩散通量的问题,弥补了Fick扩散模型的不足之处。开放型的气室很好地解决了密闭气室抑制土壤呼吸时排出二氧化碳的问题。本文将这两者相结合,进行仿真研究,并将计算结果与仿真设定的通量值进行对比,根据实验分析与计算的结果得出以下结论。
(1)土壤呼吸作为多组分扩散系统,利用Maxwell-Stefan扩散模型计算碳通量是可行的。
(2)开放型气室的设计不仅解决了抑制土壤呼吸的问题,还使气室内的二氧化碳浓度梯度呈线性趋势,能够实现对碳通量的长时间持续监测。
(3)在利用Maxwell-Stefan扩散模型计算碳通量时可以得到与实际相近的计算结果。
土壤呼吸作为一种由多组分参与的扩散过程,理论上能够运用Maxwell-Stefan模型进行计算。该模型基于浓度梯度计算碳通量,能够解决传统监测方法对二氧化碳产生抑制的问题,从而实现长时间的连续监测。为了验证该方法有效,本研究进行了2个阶段的实验;首先,分析气室内部二氧化碳浓度的动态变化。从仿真实验的结果可以看出,气室内部的二氧化碳在稳态之后呈现出稳定的浓度梯度,这使得基于Maxwell-Stefan模型计算碳通量具备可行性。之后,通过程序根据S-A湍流模型生成不同高度处的浓度时间序列进行碳通量计算,得出每一时刻下的碳通量值。通量值与设定值对比的结果表明,该方法能够得出较为准确的通量计算结果。另外,还将前述计算结果与Fick模型进行了对比。Fick模型作为Maxwell-Stefan模型的一种二元组分特殊形式,已经取得了较好的二氧化碳通量监测效果[21]。Krishna等[22]利用气井法并使用Fick模型进行土壤呼吸碳通量的计算,计算得出的最大误差在16%以内,这一精度在碳通量监测领域是非常领先的。Maxwell-Stefan因其适用于多组分扩散这一优点,应该能够取得更加精确的计算结果[23],本实验也很好地证明了这一猜想。在多组实验中,Maxwell-Stefan模型所计算出的二氧化碳通量值都比Fick模型更加接近设定值。本研究从理论和实验上同时证明了Maxwell-Stefan更加适用于计算土壤碳通量并且能够得到很好的计算结果。
本研究证明了Maxwell-Stefan模型与开放气室相结合的可行性,为后续研究土壤生态环境提供了一种新的方法。但在野外实地测量时,可能还会受到许多其他因素的干扰,解决这些问题将是今后拓展该方法实用性的重点。此外,今后应着重探讨的地方还有2点:第一,不同地区和类型的土壤中所排放的气体有所不同,利用本文模型计算时应考虑到更多的扩散组分;第二,在真实环境下测量时,水平气流的速率并不是恒定的,因此在关于野外情况下如何对浓度梯度进行拟合,还应做进一步研究。

