基于小世界网络分析的小球类专项学生运动员脑网络可塑性变化研究

杨成波 ，向 宇 ，黄 月 ，陈华富 ，3，高 晴 *

脑的可塑性指脑神经系统具有在外界环境和经验的作用下不断塑造其结构和功能的能力（Kolb et al.，2011）。运动员经历了长期的任务相关练习，相较于普通人有更强的运动、感知和决策能力（Yarrow et al.，2009）。已有研究表明，对运动员分别进行耐力和技能训练，技能组运动员的运动皮层任务相关区域产生了可塑性差异（Kumpulainen et al.，2015）。对大脑运动系统的功能和结构可塑性进行研究将帮助我们理解运动准备、运动模仿和运动学习等运动功能的神经机制，进而对运动员提出更有针对性的训练建议，提高训练的有效性。

相关神经影像学研究发现，长期训练的运动员大脑产生了可塑性变化，这种可塑性包括了大脑结构和功能的可塑性。篮球运动员的前庭小叶VI-VII体积相较普通人有所增大（Park et al.，2009）。运动员双侧前中回、左下顶叶、中央回、眼眶额回和颞上回的灰质体积明显高于非运动员，且不同运动项目具有其特异性（Hu et al.，2018）。乒乓球运动员在双侧额中回、右中眶额区等区域激活明显少于非运动员，在左颞中回、双侧舌回等区域的激活明显多于非运动员（Guo et al，2017）。羽毛球运动员技能的提升不仅与小脑中灰质密度增大的塑性结构变化有关，而且与额顶连接的功能改变有关。这种结构和功能的改变可能反映了运动员经过长期训练和练习得到的经验，包括视觉空间处理和手眼协调以及精巧的运动技能（Di et al.，2012）。这些研究结果表明，长期训练促使运动员的大脑产生了可塑性变化，建立了一个更有效率的神经网络组织。

小世界网络的概念最早由Watts等（1998）确定，是一种常见的复杂网络属性，同时兼具规则网络的高聚类系数和随机网络的低特征路径长度的特点。有研究揭示，人脑具有小世界网络组织特性，是一个高效经济的网络，因为它可以用较少的边构建，同时又能高效地传播信息（Bullmore et al.，2009，2012；Van Den Heuvel et al.，2010a）。基于图论的小世界网络分析方法能够刻画脑网络的拓扑属性，揭示大脑的工作机制，目前已普遍应用于脑功能和结构连接网络的研究中（Van Den Heuvel et al.，2010b）。

1 研究对象与方法

1.1 研究对象

在成都体育学院体育教育专业小球类专项（羽毛球/乒乓球）招募学生运动员37人（男：26人），专业训练年限少于2年，每周训练强度少于30 h。同时募集年龄和性别与学生运动员匹配的普通被试作为对照组，共45人（男：29人）。研究对象一般情况见表1，学生运动员组与对照组之间年龄和教育程度无差异。所有被试无任何神经、精神病（史），均为右利手，双眼裸眼视力或者校正视力正常。本研究经过电子科技大学伦理委员会同意，所有被试者均在磁共振检查前被详细告知本研究内容，并签署知情同意书。

表1 研究对象人口学数据Table 1 Demographics of the Subjects M±SD

1.2 实验设计及数据采集

影像数据在电子科技大学磁共振中心3.0 T超导磁共振成像系统（GE Signa MR750，美国）下采集。受试者闭目平躺于扫描仪内，嘱其保持安静，尽可能不作任何动作和意向性思维，不可睡着。结构像采用T1-SPGR序列，重复时间（repetition time，TR）6.0 ms，回波时间（echo time，TE）2.0 ms，翻转角（flip angle）12°，采集矩阵（matrix）：256×256，体素大小（voxel size）1.0 mm×1.0 mm×1.0 mm，层厚1.0 mm，无层间距（no slice gap），平行于前后联合轴位扫描，共156层包括全脑。脑静息态功能像采用GREEPI序列，采集位置复制结构像，TR 2000 ms，TE 30 ms，翻转角90°，采集矩阵：64×64，层厚3.2 mm，无层间距，共43层，体素大小3.75 mm×3.75 mm×3.2 mm，连续采集266个时间点。

1.3 数据处理和分析方法

功能磁共振数据使用Dpabi（http：//rfmri.org/dpabi）进行预处理。首先去除前10个时间点，以消除机器刚开始运行时产生的物理噪声对数据的影响。剩下的256个时间点的功能像磁共振数据，首先进行时间层校正，将时间序列其他图像的位置匹配到中间时间点的图像上，并且计算所有被试相邻时间点的头动参数。将头动参数＞2.0的被试数据剔除后，剩下37个运动员以及45个普通被试。然后将每个被试的图像配准到EPI模板上，再进行空间标准化到MNI标准空间，进行去线性漂移，滤波（0.01～0.08 Hz），接着回归掉24个头动参数，全脑信号，脑脊液，白质平均信号等协变量。

DTI数据的预处理如下：使用dcm2nii（https：//www.nitrc.org/projects/dcm2nii）将原始DICOM格式的DTI数据转换为NIFIT数据格式，NIFTI数据包含DTI数据和无磁场b0项以及不同权重的梯度向量bvecs。使用FSL（FMRIB Software Library）中的Eddy Correct工具对其b0数据进行涡流校正。然后用纤维追踪软件Diffusion Toolkit软件的FACT算法对涡流校正后的DTI数据计算每一个被试的确定性追踪，阈值设定为FA＜0.2，追踪角度＜45°。

为构建大脑结构网络，首先对T1结构像进行剥颅骨处理，设置阈值系数为0.2。然后将DTI数据匹配到个体T1数据上，将匹配后的图像再配准到MNI空间，做非线性变换F，接着利用其逆变换F-1对MNI空间的AAL模板进行变换，得到每个被试基于自身划分的90个脑区。将这90个脑区作为网络的节点，将每个区域的平均各向异性分数mean_FA值进行Fisher_Z变换以提高其正态性，所得值作为网络的边，得到每个被试的大脑结构网络矩阵。

为构建大脑功能网络，使用静息态磁共振功能图像，以AAL模板定义的90个大脑区域作为节点，计算这些区域内的平均时间序列信号来代表该脑区的时间序列信号，并计算每个被试脑区之间时间序列信号的皮尔逊相关值，再对这些相关值进行Fisher_Z变换，这些变换后的相关值构成了网络的边，最终每个被试都有一个90×90的对称相关矩阵，代表每个被试的大脑功能网络矩阵。

一个网络G定义为一个有序对，G=（V，E），其中V表示顶点集，E为边集。也可以用一个|V|×|V|邻接矩阵A=[aij]表示。

节点度（degree）表示与某一个顶点直接连接的边的数目。局部聚合系数（clustering coefficient）表示节点的邻居节点间实际存在的边数与可能存在最大边数的比值。

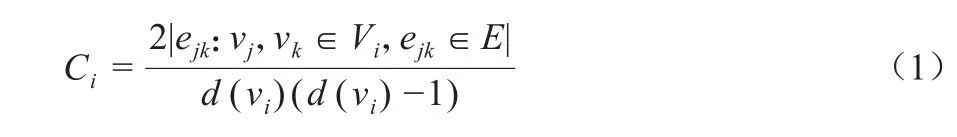
将所有节点的聚合系数除以节点总数得到全局聚合系数，全局聚合系数反映了一个网络的聚合程度（Watts et al.，1998）。

特征路径长度（shortest path length）描述的是整个网络的信息传输效率能力，通常用L表示，表示的是整个网络中最短路径长度的平均值（Newman，2003）：

网络G的平均路径定义如下：

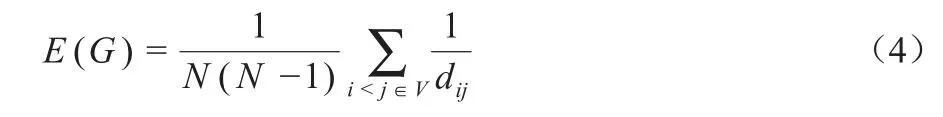
全局效率（global efficiency）代表一个网络的通信能力，和平均路径长度成正相关关系，定义为：

其中，E(Gideal)表示完全图G的平均路径，计算可得E(Gideal)=1。

局部效率（local efficiency）表示一个网络的容错能力，表示去掉某个节点后，与这个节点直接相连的节点所构成的子图的信息传输能力（Boccaletti et al.，2006；Bullmore et al.，2009），定义为：

其中，Gi表示与节点i直接相邻的节点所构成的子图（不包含节点i）。

标准化后的聚类系数和特征路径长度的比值σ可以用来衡量一个网络是否为小世界网络，定义为：其中Crandom和Lrandom分别是1 000个随机网络的平均聚类系数和平均特征路径长度。若求得γ≫1，λ≈1，σ≫1，则可以判定此网络是小世界网络（Humphries et al.，2006）。

网络属性如聚类系数等的计算依赖于网络的边数，所以不能将具有不同边数的网络的指标直接进行对比。对原始网络施加一个阈值可以使得不同网络具有相同数量边的同时使得网络具有稀疏性。稀疏度选择的下限是保证所有被试的平均度＞2logN，N代表网络节点的个数，稀疏度选择的上限为所有被试的结构网络稀疏度最小值。在此阈值范围内，能保证取阈值后的网络具有小世界属性的同时减少假阳性影响（Bullmore et al.，2011；Long et al.，2013）。经过计算，本研究选择的阈值范围为：0.03≤s≤0.15。为比较运动员与普通被试的小世界网络属性差异，在不同阈值下对聚类系数C、特征路径长度L、全局效率Eg、局部效率Eloc、节点效率Enodal等网络属性，以及小世界网络指标γ、λ、σ进行计算。网络拓扑属性的计算在GRETNA工具包中进行（Wang et al.，2015）。

2 结果

本研究对小球类专项学生运动员组和对照组的大脑结构和功能连接网络的图论指标（标准化聚类系数γ，标准化最短路径长度λ，小世界属性σ，全局效率Eg，节点效率Enodal，聚类系数Cp，局部效率Eloc）之间的差异进行统计分析。如图1、2所示，小球类专项学生运动员和普通被试的大脑结构网络及功能网络都呈现出了小世界拓扑特性，即Y>1，λ≈ 1，α>1。

小球类专项学生运动员与普通被试功能和结构网络的全局效率和节点效率没有明显差异，聚类系数及局部效率随稀疏度变化情况如图3、4所示。

稀疏度≈0.09，运动员和普通被试的全局聚类系数以及局部效率有明显差异。稀疏度＜0.09，对两组被试的全局聚类系数和局部效率进行双样本t检验，结果如图5所示。将这一稀疏度下小球类专项学生运动员的结构网络和功能网络的网络属性进行耦合，结果显示，结构和功能网络下的全局聚类系数具有显著相关关系（r=0.33，P＜0.05）。

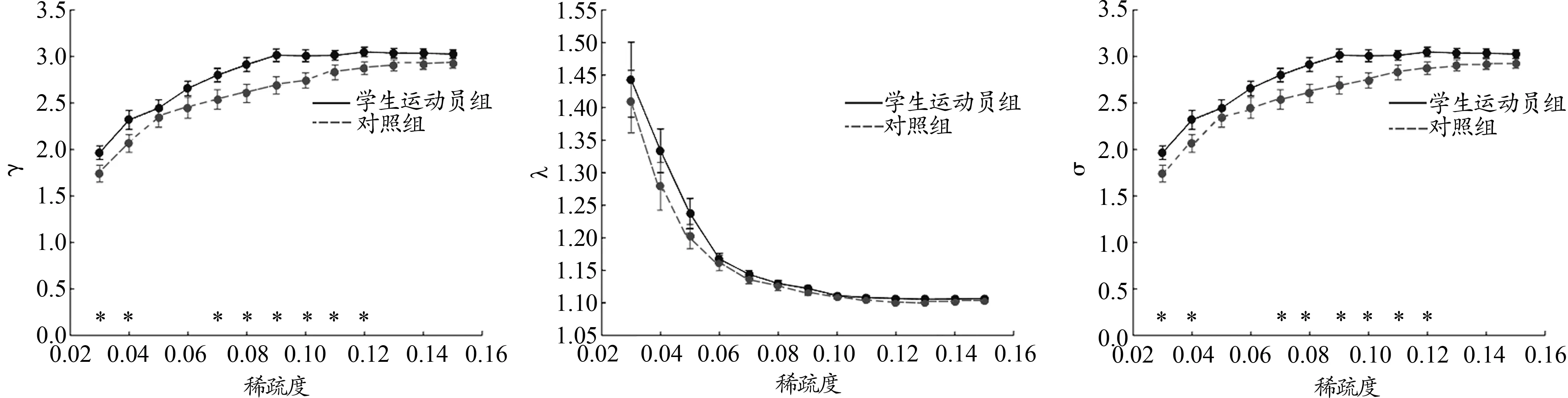
图1 结构网络小世界属性随稀疏度变化图Figure 1. The Small-world Property of Structural Network with Different Sparsity

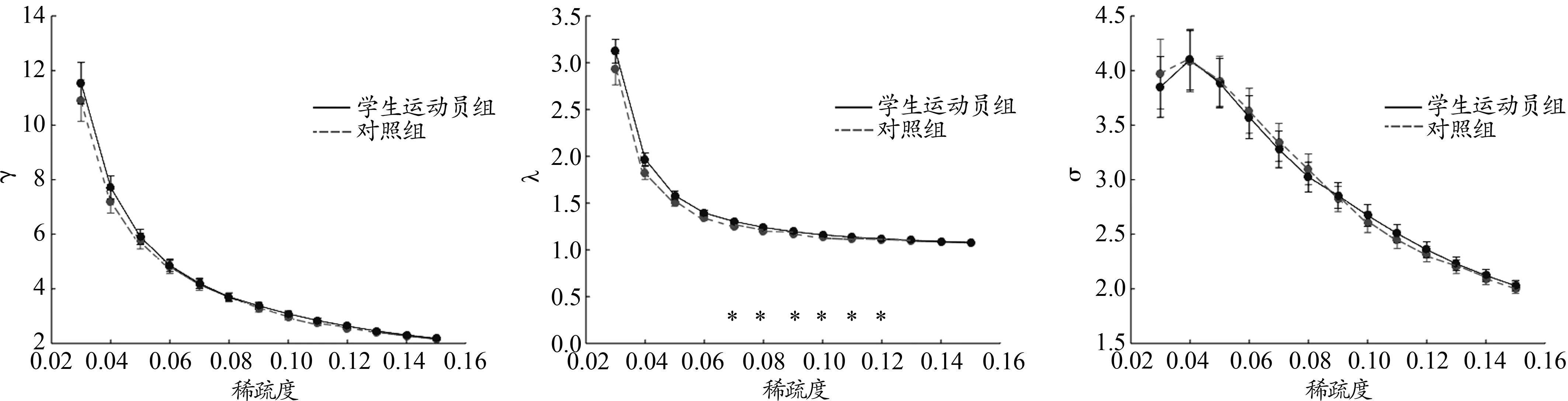
图2 功能网络小世界属性随稀疏度变化图Figure 2. The Small-world Property of Functional Network with Different Sparsity

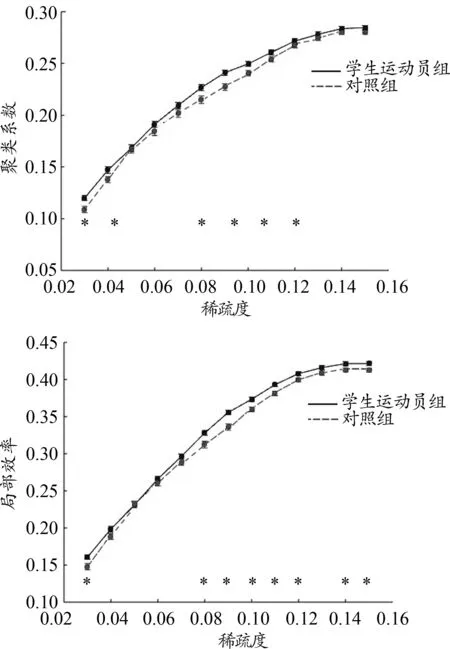
图3 结构网络聚类系数以及局部效率随稀疏度变化图Figure 3. The Clustering Coefficient and Local Efficiency of Structural Network with Different Sparsity

3 讨论

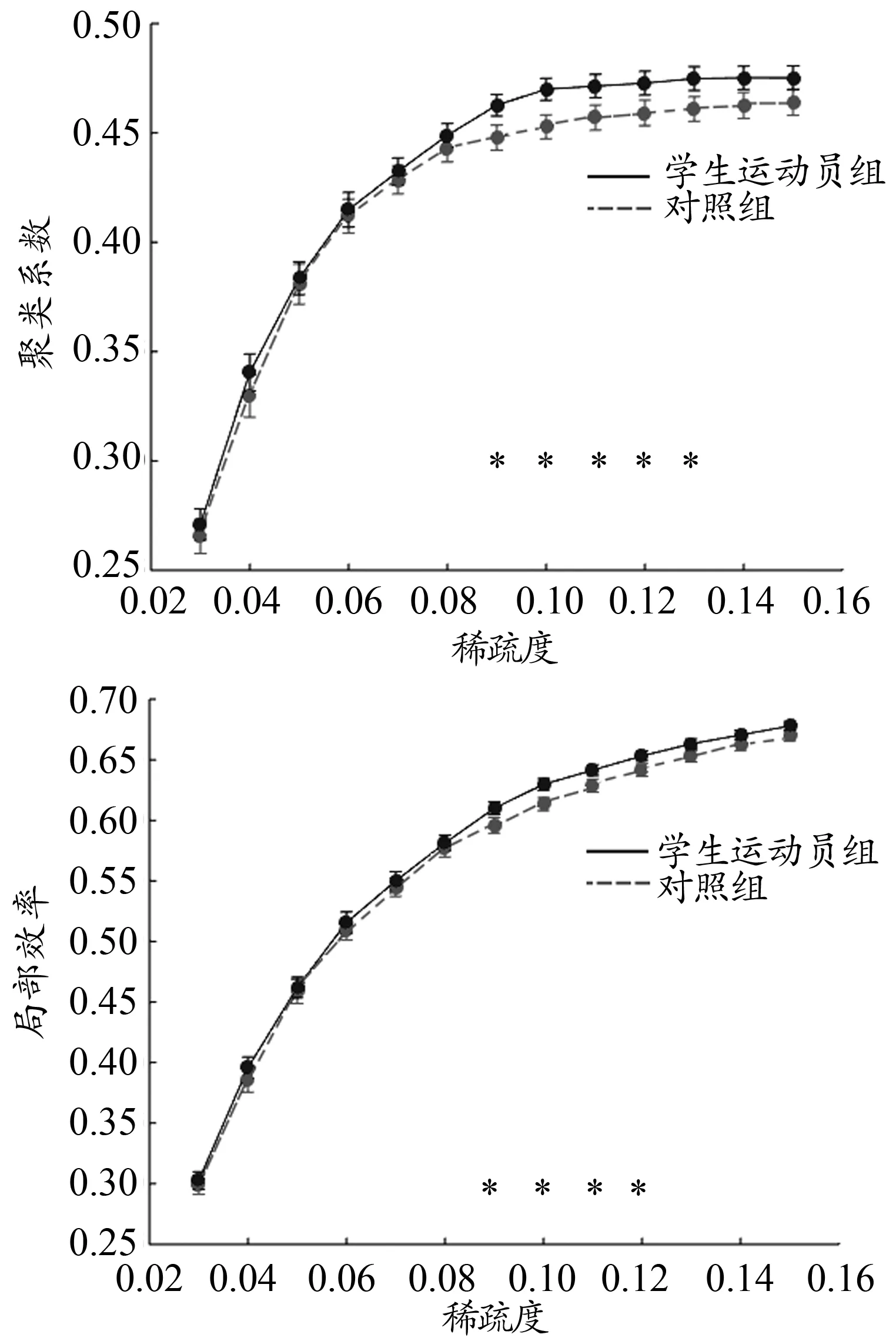
图4 功能网络聚类系数以及局部效率随稀疏度变化图Figure 4. The Clustering Coefficient and Local Efficiency of Functional Network with Different Sparsity

小世界网络兼具规则网络的高聚类系数和随机网络的低特征路径长度的特点，是一种稀疏且高效的网络。小世界网络与随机网络相比，具有较大的全局聚类系数和较短的平均路径长度；与规则网络相比，具有较短的特征路径长度（Watts et al.，1998）。一般将标准化后的聚类系数和特征路径长度的比值σ作为衡量一个网络是否为小世界网络的标准。若σ趋于1，则该网络为小世界网络（Bullmore et al.，2009）。本研究使用了小世界网络方法探究小球类专项学生运动员脑的结构和功能网络的可塑性变化。结果显示，小球类专项学生运动员与普通被试的结构及功能网络都呈现出小世界特征，这与前人的研究结果一致（Di et al.，2012；Iturria-Medina et al.，2008）。

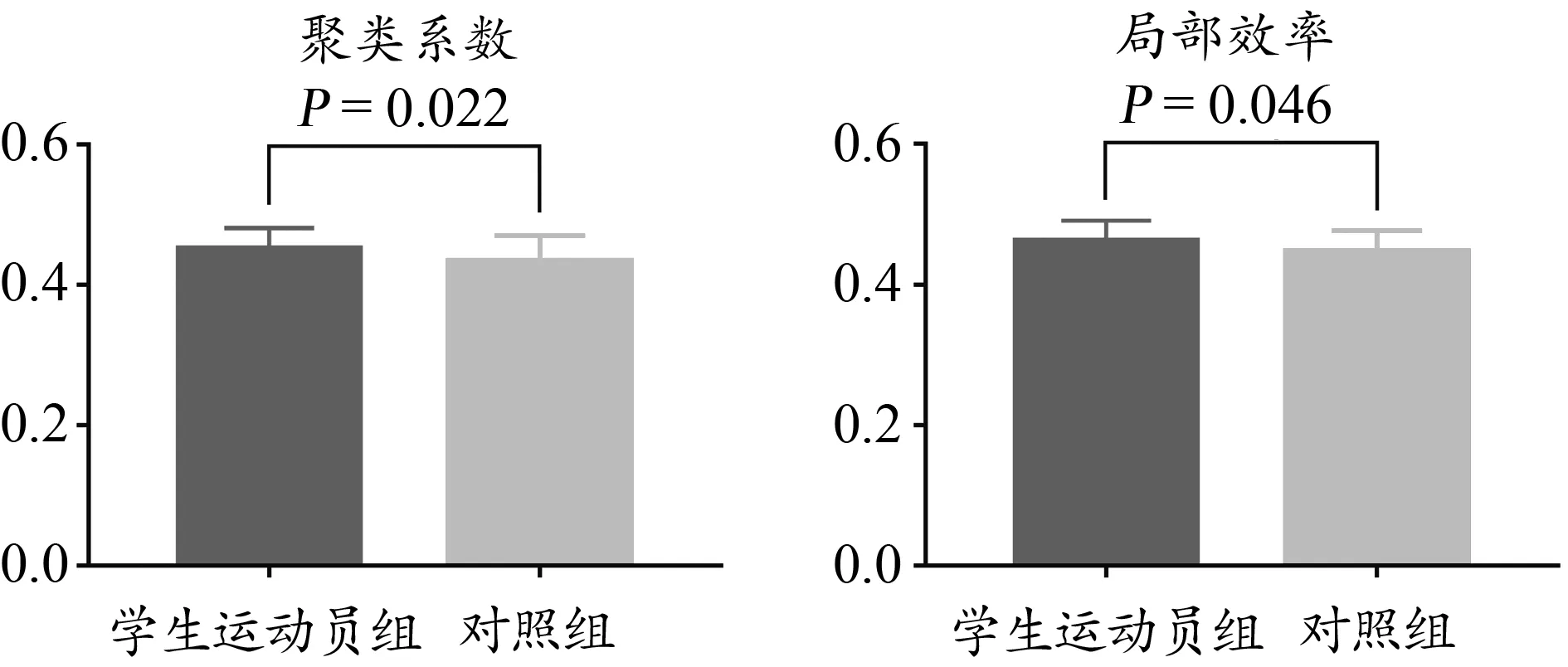
图5 小球类专项学生运动员和普通被试整体网络参数比较结果（稀疏度=0.09）Figure 5. The Group Difference of the Clustering Coefficient and Local Efficiency Between theAthlete Group and the Control Group

在结构网络中，小球类专项学生运动员标准化后的平均聚类系数和平均最短路径，以及小世界属性都比普通被试高；在功能网络中，小球类专项学生运动员标准化后的平均聚类系数和平均最短路径高于普通被试。聚类系数反映了节点与其相邻节点间的聚集程度，最短路径表示两个节点进行通信所需经过的最短路径长度。较高的平均聚类系数值意味着网络中节点间的连接更为紧密。较短的平均最短路径则意味着网络中节点间的信息传递更加迅速（Bullmore et al.，2009；Sporns，2013）。这表明，运动员通过长期训练，其脑网络容错能力更强，信息传递更加迅速有效。

对原始的功能网络和结构网络进行稀疏化可以使得后续网络属性计算更专注于有效连接。具体做法是，将网络中的边进行排序，施加一个阈值，使其保留一定百分比的较大边，这个阈值被称为稀疏度。网络的拓扑属性与其稀疏程度有关，因此，对不同稀疏度下的网络属性进行探究和比较是必要的（Kumpulainen et al.，2015）。在对不同稀疏度下的结构网络和功能网络进行研究中发现，小球类专项学生运动员的全局聚类系数和局部效率整体上都比普通被试高，且在部分稀疏度下表现出明显差异。这可能意味着小球类专项学生运动员在不同稀疏度下的脑有效连接都比普通被试多，脑区之间通信更加迅速有效，信息容错能力更强。由此说明，小球类专项学生运动员通过一段时间的运动训练，大脑出现了一些改变，在信息传输速度和信息整合能力等方面有所提高。

当稀疏度为0.09时，小球类专项学生运动员与普通被试脑网络的聚类系数和局部效率差异显著，且结构和功能网络下的聚类系数具有显著相关关系。运动员大脑的结构和功能密不可分，结构是功能的基础，功能是结构的表征（Abdelnour et al.，2018；Koch et al.，2002）。已有研究证明，功能连接是结构连接的直接反应，反之也能根据不同的需求（如某种长期的特殊训练或病理状态）对结构连接产生可塑性影响（Greicius et al.，2009；Phillips et al.，2012）。结构网络和功能网络的聚类系数呈现出正相关关系，这为结构网络和功能网络的相互影响即大脑的可塑性提供了证据。

图6 小球类专项学生运动员结构和功能聚类系数耦合结果Figure 6. The Coherence of the Clustering Coefficients of Structural and Functional Networks

4 结论

小球类专项学生运动员大脑的结构网络及功能网络的聚类系数和局部效率比普通被试高，且结构和功能网络的全局聚类系数显著协变，说明，运动训练引起小球类专项学生运动员的脑功能网络和结构网络的连接更多，脑区之间通信更加迅速有效，信息容错能力更强。