频段内汽车悬架时滞反馈控制参数优化

刘建均 孙艺瑕 李胜

摘 要：对有限频段内汽车悬架系统的时滞反馈控制参数优化问题进行研究。首先，建立时滞加速度反馈控制下1/4汽车悬架系统力学模型，推导出车身和车轮加速度幅值的解析表达式;其次，通过对系统稳定性分析，得到关于反馈增益系数和时滞的稳定性分区图，以数值计算验证稳定性分析的正确性;最后，在有限频段内以最大车身加速度变化的百分比为优化目标，以反馈增益系数和时滞为优化参数，利用粒子群优化算法获得有限频段内最优反馈增益系数和时滞。实验结果表明，与被动汽车悬架系统相比较，最优时滞反馈控制下汽车悬架系统的隔振性能获得了明显提高，在最优时滞反馈控制参数取值下，有限频段内车身加速度幅值至少降低37.27%。

关键词：汽车悬架系统;有限频段;时滞反馈控制;参数优化;隔振性能

DOI：10. 11907/rjdk. 191819 开放科学（资源服务）标识码（OSID）：

中图分类号：TP319文献标识码：A 文章编号：1672-7800（2020）005-0102-05

0 引言

汽车悬架系统隔振性能是影响汽车行驶平顺性和乘坐舒适性的重要因素。传统被动悬架系统虽然有结构简单成本低等优点，但难以适应复杂的路况，而主动悬架系统却能根据路况和汽车的运动状态，适时调节悬架系统参数，改善汽车悬架系统性能[1]。然而，由于控制信号的采集传输和控制力计算等因素，主动系统不可避免存在时滞现象。时滯对汽车悬架系统控制的影响不容忽视，可能会影响控制效果，甚至失稳[2]。目前，对汽车主动悬架系统中的时滞问题研究主要通过时滞补偿技术与现代控制技术相结合，以提高主动控制系统的稳定性和汽车悬架系统的隔振性能[3-6]，且大部分是在全频域进行控制研究。文献[7]指出汽车乘坐的舒适性仅与人体敏感频段4～8Hz内的车身加速度幅值相关。已有研究[8-10]表明，与全频域内汽车悬架系统控制策略相比，有限频段内的控制策略效果更佳;陈长征等[11]针对预瞄控制中的时滞问题，提出了一种与时滞相关的有限频段内线性变参数控制，通过研究证明有限频段内的控制效果优于全频内的控制效果;张进秋等[12]在主动悬架有限频域H∞时滞控制基础上引入一种单神经元PID和无辨识PSD调节算法相结合的优化算法。仿真结果表明，与未加优化算法的控制策略相比，该控制策略使有限频段内车身加速度明显降低，进一步提高了车辆舒适性和平顺性。

本文在有限频段内对时滞加速度反馈控制下的汽车悬架系统进行控制参数优化，以反馈增益系数和时滞为优化参数，采用粒子群优化算法对有限频段内车身的加速度幅值变化百分比进行优化，获得两参数的最优值，从而最大程度地提高汽车悬架系统的隔振性能。

1 力学模型

图1所示为时滞反馈控制下1/4汽车悬架系统的力学模型。ms表示簧载质量是车身、车架及其上面的总成;簧载质量通过弹簧和减振器与车轮和车轴相连，弹簧刚度为ks，减振器阻尼为cs;mu为非簧载质量，由车轮和车轴等组成，车轮经过具有一定线性刚度kt和阻尼ct的轮胎支撑在不平的路面上;[zs]和[zu]分别表示车身、车轮在竖直方向上的位移，[zr]为路面激励[13]，[zr=rsin（ωt）]，其中r、[ω]分别为路面激励的幅值和频率;[u（t-τ）]为簧载质量与非簧载质量之间的时滞反馈控制力，[u（t-τ）=gz1（t-τ）]，其中g和[τ]分别表示反馈增益系数和时滞，其中时滞包括固有时滞和主动时滞。

2 稳定性分析及数值验证

2.1 稳定性分析

1/4汽车悬架系统结构参数[14]如表1所示。

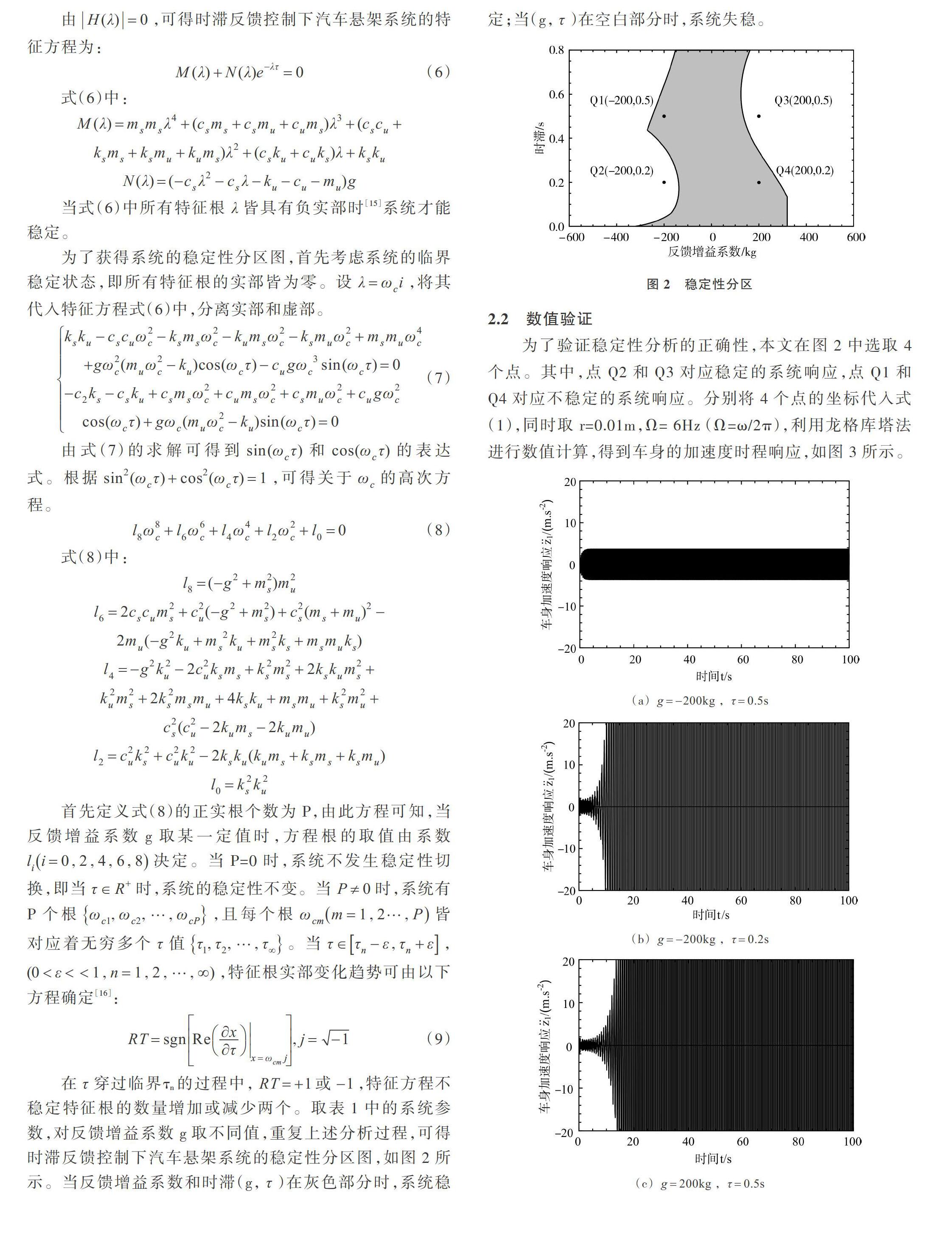
在[τ]穿过临界τn的过程中，[RT=+1]或[-1]，特征方程不稳定特征根的数量增加或减少两个。取表1中的系统参数，对反馈增益系数g取不同值，重复上述分析过程，可得时滞反馈控制下汽车悬架系统的稳定性分区图，如图2所示。当反馈增益系数和时滞（g，[τ]）在灰色部分时，系统稳定;当（g，[τ]）在空白部分时，系统失稳。

2.2 数值验证

为了验证稳定性分析的正确性，本文在图2中选取4个点。其中，点Q2和Q3对应稳定的系统响应，点Q1和Q4对应不稳定的系统响应。分别将4个点的坐标代入式（1），同时取r=0.01m，Ω= 6Hz （Ω=ω/2π），利用龙格库塔法进行数值计算，得到车身的加速度时程响应，如图3所示。

3 频段内控制参数优化与验证

3.1 频段内控制参数优化

为了分析最优控制参数对频段 4～8Hz范围内汽车悬架系统的隔振性能影响，定义车身加速度变化的百分比[Φ]如式（10）所示。

由图2可将待优化的时滞反馈控制参数g和τ分别限制在[-200，300]kg与[0.01，0.8]s范围内，以[Φ]为适应度函数，利用粒子群优化算法进行优化问题求解，获得最优控制参数（最优反馈增益系数gop和最优时滞τop），以及频带内最优时滞反馈控制下车身和车轮的加速度幅值变化情况。

优化参数设置如下： 粒子数为500，空间维数为1，最大迭代次数为1 000，学习因子为0.9，惯性权重为0.8，速度限制为[-1，1]，位置限制为[4，8]。

优化结果如图4和图5所示。

3.2 优化结果验证

为了验证频段内优化结果的正确性，取频率[Ω=8Hz]处的最优结果进行数值验证，验证结果如图6所示。

4 结语

本文使用粒子群优化算法对1/4汽车悬架系统中频段内时滞反馈控制参数优化问题进行了研究，得到如下结论：①在频段内最优时滞反馈控制参数取值下，汽车悬架系统的隔振性能得到一定程度的改善。在人体敏感频段4～8Hz范围内，车身加速度幅值至少降低37.27%;②与被动汽车悬架系统相比，在频段内最优时滞反馈控制参数取值下，车身加速度幅值减小，车轮加速度幅值增大，表明两者之间存在能量传递。

本文不足之处是只采用数值模拟方式对研究结果进行验证。后续将考虑通过汽车悬架系统实验进一步验证频段内最优时滞反馈控制参数对汽车悬架系统隔振性能的影响。

参考文献：

[1] 潘公宇，任萍丽.  汽车振动学基础及其应用[M]. 北京：北京大学出版社，2013.

[2] 蔡国平， 陈龙祥. 时滞反馈控制及其实验[M]. 北京：科学出版社，2017.

[3] 王飞，周继磊， 任传波. 时滞反馈下非线性悬架系统的减振特性研究[J]. 广西大学学报， 2016，41（2）：379-387.

[4] HAN S Y，ZHANG C H，TANG G Y. Approximation optimal vibration for networked nonlinear vehicle active suspension with actuator time delay[J].  Asian Journal of Control， 2017， 19（3）：983-995.

[5] FEI W，ZHOU J，REN C. Research on chaotic dynamics properties for nonlinear suspension system with time-delay[J]. Chinese Journal of Applied Mechanics， 2016， 33（5）：891-897.

[6] BOUOUDEN S，CHADLI M，ZHANG L， et al. Constrained model predictive control for time-varying delay systems： application to an active car suspension[J]. International Journal of Control Automation & Systems， 2016， 14（1）：51-58.

[7] 余晨光，鄧宝清. 汽车理论[M]. 长沙：中南大学出版社， 2016.

[8] SUN W，ZHAO Y，LI J，et al. Active suspension control with frequency band constraints and actuator input delay[J]. IEEE Transactions on Industrial Electronics， 2012， 59（1）：530-537.

[9] WANG R，JING H，YAN F，et al. Optimization and finite-frequency H∞ control of active suspensions in in-wheel motor driven electric ground vehicles[J].  Journal of the Franklin Institute， 2015， 352（2）：468-484.

[10] SUN W， LI J， ZHAO Y， et al. Vibration control for active seat suspension systems via dynamic output feedback with limited frequency characteristic[J].  Mechatronics， 2011， 21（1）：250-260.

[11] 陈长征， 王刚，于慎波.  考虑时变输入时滞及频段约束的车辆主动悬架预瞄控制[J].  机械工程学报， 2016， 52（16）： 124-131.

[12] 张进秋，王兴野，贾进峰， 等.  主动悬架有限频域H∞时滞控制参数影响分析及优化[J].  兵工学报， 2018， 39（9）：189-196.

[13] WANG S，HUA L，YANG C， et al. Nonlinear vibrations of a piecewise-linear quarter-car truck model by incremental harmonic balance method[J].  Nonlinear Dynamics， 2018， 92（4）：1719-1732.

[14] SUN W，GAO H，KAYNAK O. Finite frequency control for vehicle active suspension systems[J]. Control Systems Technology IEEE Transactions on， 2011， 19（2）：416-422.

[15] 闫茂德，高昂， 胡延苏.  现代控制理论[M]. 北京： 机械工业出版社， 2016.

[16] OLGAC N， SIPAHI R. An exact method for the stability  analysis of time-delayed linear time-invariant （LTI） systems[J].  IEEE Transactions on Automatic Control， 2002， 47（5）：793-797.

（责任编辑：杜能钢）