初中数学图形等面积拼接问题的教学探究

【摘要】本文論述初中数学图形等面积拼接问题的教学方法，建议教师在教学中做好该问题题型的研究，做好相关例题的选择与讲解，让学生掌握图形等面积拼接的方法与技巧，提高学生解决该类问题的能力，提升其数学素养。

【关键词】初中数学 图形 等面积拼接问题 教学探究

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2020）05A-0098-02

为解决图形等面积拼接问题，学生需要对相关图形的构成元素有深刻的认识，具备良好的平面、空间图形想象能力。教师应做好经验总结，把握教学重难点，积极采取有效的教学措施，不断提高学生学习的积极性与主动性，使其掌握各类图形等面积拼接问题的解题思路，进而真正地攻克该类问题。

一、结合例题做好拼接引导

初中数学图形等面积拼接问题灵活性较强，为避免挫伤学生的学习积极性，增强学生的自信心，教师在教学中应注重结合具体例题，做好拼接引导，使学生亲身感受拼接思路，给其留下深刻印象，指导其更好地解决类似的问题。一方面，教师应从整体上对初中数学涉及的图形等面积拼接问题进行总结，结合学生所学内容以及实际情况，借助多媒体技术展示相关的例题，并动态化地呈现拼接的过程，使学生感受拼接前后图形形状与位置的变化。另一方面，教师应围绕例题与学生积极互动，营造活泼的课堂氛围，鼓励学生寻找图形拼接的新思路，锻炼学生思维的灵活性。此外，教师还要根据学生在听课中的表现，及时给予表扬与肯定，提高其拼接学习的体验。

教学中教师可借助多媒体课件为学生讲解以下例题：如图1所示，用8块A形瓷砖（白色四边形）和8块B型瓷砖（黑色三角形），不重叠，无缝隙拼接成一个正方形图案，则图案中A型瓷砖的总面积和B型瓷砖的总面积之比为（  ）.

该题目较为新颖，主要考查了图形的拼接和正方形的性质。在解答这道题时，充分理解题意、合理地作辅助线是顺利解题的关键。为使学生快速找到该题型的解题思路，教师要引导学生通过作辅助线寻找突破口，接着重点讲解解题过程，使学生充分感受具体的解题思路。如图1所示，分别作DC⊥EF于C，DK⊥FH于K，连接DF.考虑到四边形DCFK是正方形，则满足∠CDM=∠MDF=∠FDN=∠NDK，因此，∠CDK=∠DKF=90°，DK=FK，DF=[2]DK.此时使用面积法不难证明角平分线的性质定理，得出S△DFN/S△DNK=FN/NK=DF/DK=[2]，所以，SA型/SB型=2S△DFN/2S△DNK=[2]，即图案中A型瓷砖的总面积和B型瓷砖的总面积之比为[2][∶]1，正确选项为A。通过该类题目的讲解，学生认识到认真审题、通过作辅助线找到图形之间的内在联系是解答该类题型的重要思路。

二、注重实践激发拼接兴趣

在初中数学图形等面积拼接教学中，为给学生留下深刻的印象，激发其拼接兴趣，教师应围绕所学知识积极开展相关的实践活动，在丰富教学内容的同时，避免学生在学习中产生枯燥感。一方面，结合学生拼接知识掌握情况，布置相关的图形拼接实践任务，为学生详细阐述实践的任务和要求，而后将班级学生分成若干小组，以小组为单位开展实践任务。为保证实践任务的顺利完成，教师鼓励小组成员之间相互协作，积极动脑，不断地进行尝试。另一方面，为激发学生参与拼接活动的积极性，增强其团队意识以及荣誉感，根据各小组图形拼接任务完成情况，选出优胜的小组，给予表扬，并将其完成的作品在班级宣传栏予以展示，使他们品尝到图形等面积拼接的成就感。

教学中为激发学生的拼接兴趣，教师可以给学生布置如下实践习题：将正方形纸片以适当的方式折叠一次，沿折痕剪开后得到两块小纸片，用这两块小纸片拼接成一个新的多边形（不重叠、无缝隙），动手操作看能否使用这两块小纸片拼接成如下图形：（1）等腰直角三角形;（2）对角互补的四边形;（3）五边形;（4）六边形。

在课堂上给学生留足动手操作的时间，并将班级学生分成四个小组进行实践、验证;各小组学生积极动脑思考、动手裁剪、拼接。正方形被剪的情况可分为三种：等腰直角三角形、梯形、全等梯形。经过各小组的拼接尝试，最终得出如下结论：如将正方形剪成两个等腰直角三角形，则可将其拼接成一个等腰直角三角形;若将正方形剪成两个梯形可拼接成对角互补的四边形;若将正方形剪成两个全等的梯形，则可以拼成五边形或六边形。这样教学，通过在课堂上开展上述拼接实践活动，使得课堂氛围被激活，学生积极动脑、动手，大大降低了学生学习的枯燥感，加深了学生对图形拼接的认识与理解，圆满地完成了实践任务，收获了预期的实践效果。

三、加强训练积累拼接技巧

在图形等面积拼接教学中，为了使学生掌握相关的拼接技巧，遇到相关问题能够少走弯路，及时找到拼接的最佳途径，教师应加强训练，让学生在训练中不断地出错，然后思考出错的原因并改正，进而逐渐掌握图形等面积拼接技巧。一方面，制订明确的图形等面积拼接教学目标，合理安排训练课时，积极组织学生开展专项训练活动。为保证训练质量，教师要做好每一道训练习题的筛选，规定好训练时间，要求学生独立思考，冷静分析，充分利用生活经验以及所学知识进行解答。另一方面，针对训练中难度较大的习题，教师应注重通过设计相关问题，在课堂上与学生积极互动，给其带来解题方法的启发，使其能够尽快找到解题突破口。同时，教师还要注意走下讲台，了解学生习题完成情况，及时给予针对性的指导，提高其训练体验。

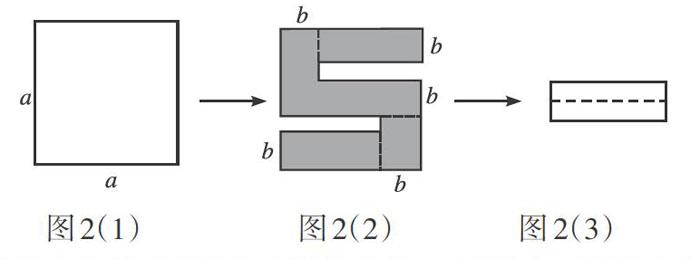
为使学生掌握图形等体积拼接的技巧，教学中可给学生出示如下训练题：将一个边长为a的正方形纸片剪掉两个长方形，得到一个“S”图案[如图2（2）]，再将剪下的两个长方形拼成一个新的长方形[如图2（2）]，则新的长方形的周长为（  ）.

A.4a-8b   B.2a-3b   C.2a-4b   D.4a-10b

题目看似难度较大，无从下手。学生在解答该题时应保持良好的心态，不要被题干中的描述所迷惑，而应找到拼接前后变与不变的量，从整体上进行分析。要求解新的长方形的周长，需要分别求出其长和宽，根据周长=（长+宽）×2，即可得出最终的结果。观察图2（2）中的上、下两条边和剪去长方形长之间的关系，可知剪去的小长方形的长=a-b.从整体上认真观察图2（2）的左边和右边，可知新长方形的宽=a-3b，则其周长=2（2a-4b）=4a-8b.正确选项为A.通过该题目的训练使学生认识到解答该类问题时应牢牢把握图形拼接前后面积不发生变化，而其长和宽可能发生变化。而后认真分析，找到拼接前后参数之间的关系，从而快速解答。

四、归纳总结提升拼接水平

为提高学生图形等面积拼接水平，除了做好教学工作，还应鼓励学生做好拼接总结，汇总图形等面积拼接题型以及在拼接解题时的不足，积极采取针对性措施，弥补知识薄弱点。一方面，鼓励学生做好经典习题的摘抄，做好习题的深入剖析，积极开展“好题重做”活动，真正做到会一题而会一类题，提高解题效率。同时，做好錯题的总结，认真分析错误原因，是习题难度较大还是思路未打开，并在习题下详细地写出正确的解题过程，掌握拼接的关键。另一方面，完成图形等面积总结后，还要在课堂上预留一些时间，鼓励学生积极交流，相互分享拼接经验与技巧，明确一些题型中拼接的注意事项，避免在解题时陷入出题人的陷阱，更好地实现拼接水平的提升。

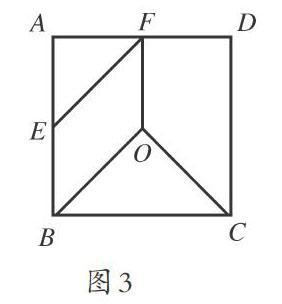
教学中教师发现学生解答如下题目时出错率较高，于是要求学生认真分析，找到错误所在，及时纠正，并总结解题技巧，避免遇到类似题目再次出错：如图3所示，正方形ABCD的边长为2，然后将正方形ABCD分割成如图中的四块。其中点O为正方形的中心，点E、F分别是AB、AD的中点，用这四块纸片拼成一个与正方形不全等的四边形MNPQ（要求不重叠，无缝隙），则四边形MNPQ的边长是    。

该题目题干并不难理解，但要想正确作答并非易事。笔者在教学中发现，很多学生在解答过程中容易考虑不全而出错。教师通过鼓励学生积极思考、讨论，并给予引导，最终得出拼接后的图形有四种情况（如下图所示）：

其中图4（1）为等腰梯形，对照图3中各边情况可知其上底长为3，下底长5，两腰长为[2].图4（2）为平行四边形，长边长为4，短边长为[2].图4（3）为长方形，对应的长和宽分别为4和1.图4（4）为直角梯形，上、下底长分别为1、3，两条腰长分别为2[2]和2.通过对该题目的分析使学生认识到解答该类习题时，为保证结果的正确性，应冷静分析，充分考虑每一种可能的情况，并通过绘制草图辅助分析。

综上所述，在初中数学教学中，学生能否顺利解决图形等面积拼接问题，一定程度上关系着其数学学习成绩的提高，因此教师应提高认识，结合自身的教学经验，做好相关教学策略的研究，既要结合例题做好拼接教学引导，又要注重结合实践激发学生的拼接兴趣。同时，还应做好习题的筛选，做好拼接训练，使学生积累各种拼接技巧。另外，鼓励学生做好学习总结，借鉴他人的成功经验，弥补自身的不足，不断提升拼接水平。

作者简介：马德林（1974— ），广西贺州人，大学本科学历，高级教师，长期从事中学数学教育教学研究。

（责编 林 剑）