基于流固耦合法的储罐地震响应分析
翁 羽, 邓志安,刘佳伦,潘 杰,吴 刚
(西安石油大学,陕西 西安 710065)
0 引言
早在上世纪中期,研究者就开展了刚性储液罐的液体晃动研究。Housner[1]提出了基于刚性罐壁假设的储液罐晃动流体域固体耦合问题的质量-弹簧系统的简化模型。Haroun[2]使用弹性壳单元模拟罐体,流体部分使用附加质量法,从而获得了改进的储液罐地震响应分析方法。Broc等[3]使用ALE(Arbitrary Lagrangian Eulerian)描述法与有限元法结合,来求解瞬态流固耦合问题。Amabili等[4-5]针对该问题使用势函数分解法进行分析,假设液体为理想流体、储液罐为刚性。国内也有学者使用不同方法进行相关研究[6-8]。在能源领域,Sigrist等[9-10]使用均质模型来考虑流体及结构间的相互耦合作用,并成功将该方法用于各类承压容器。
本文旨在使用CFD和FEM交替耦合的数值分析方法研究储罐在地震条件下的内部流体晃动和结构响应特性,分析中考虑更为真实的气液两相黏性湍流态流体与结构之间的相互作用。
1 研究方法
1.1 研究模型
本文研究的储罐采用卧式布置,设计运行压力为0.3 MPa,本分析选取容器典型液体装量(50%装液量)作为分析条件。容器剖开示意图如图1所示。
对于结构计算模型和流动计算模型,网格剖分根据不同离散方法分别生成,分别使用四边形壳单元和六面体单元进行网格划分,其中FEM模型网格数量为60 000,CFD模型网格数量为3 790 000。储罐计算网格模型如图2所示。
1.2 数值计算方法
本文使用交替法由流体CFD程序和固体FEM程序分别在独立的控制区域求解[11-13],两者分别用于计算两相流体瞬态运动和固体结构瞬态变形。流固耦合的流程如图3所示,CFD和FEM计算的数值模型选取如表1和表2所示。

图1 储罐结构示意图
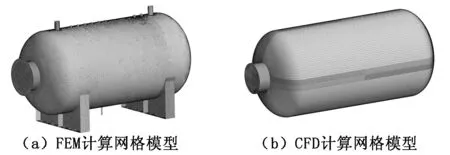
图2 储罐计算网格模型
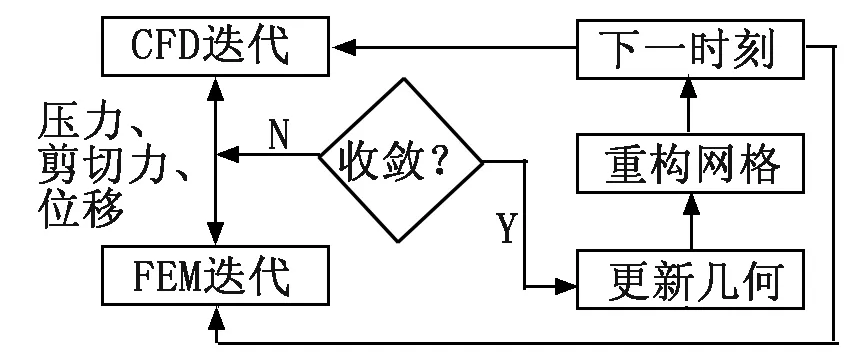
图3 流固耦合流程示意图
在计算中,CFD多相流控制方程主要包含质量守恒和动量守恒方程:
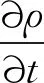
(1)
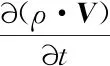
(2)
其中:ρ为密度;t为时间;为微分Hamilton算子;V为速度矢量;P为压力;S为质量源项;μ为黏度;T为温度;g为重力加速度;Tσ为相界面上的表面张力。各物理量为混合相参量。
FEM计算中主要控制方程为:
[B]=[φ][N].
(3)
{ε}=[B][D].
(4)
{σ}=E{ε}.
(5)
其中:[B]为单元应变矩阵;[φ]为四维(时间、空间)梯度矩阵;[N]为单元形状函数;{ε}为应变向量;[D]为节点位移矩阵;{σ}为应力向量;E为弹性模量。

表1 CFD数值计算模型选取

表2 FEM数值计算模型选取
1.3 计算条件
本研究并不需要考虑流体的化学属性,因此近似将流体介质考虑为热工物性接近的纯净物,其中液相为不可压缩流体,气相为理想气体。本研究选取当地基准地震谱的典型时程数据进行计算,计算选取10 s时长。地震加速度时程曲线如图4所示。
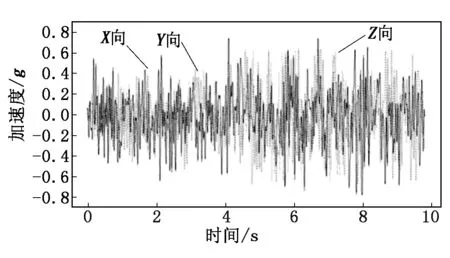
图4 地震谱时程曲线
2 结果及分析
2.1 耦合法计算结果
分析得到的容器壁位移分布如图5所示,容器内自由液面分布如图6所示。由于地震加速度在初始一段时间内幅值较小,直接造成的容器及其支承结构的变形量并不大,从而导致的流体晃动不明显,如图5、图6中(a)和(b)所示。当时间达到5 s时,液体晃动幅值显著增大;对于容器结构响应,位移量显著增大;这一阶段的结构响应增加主要是由于液体晃动作用导致,如图6(c)所示;图5(c)中容器位移的高、低频位移脉动同时出现的特性也是该现象的体现。在7 s之后,图5(d)中“波浪”在上升至容器最高点后开始有液体团垂直落入液体自由表面。图7为波浪高度变化情况,在7 s后的波谷变化反而不如5 s左右时剧烈。
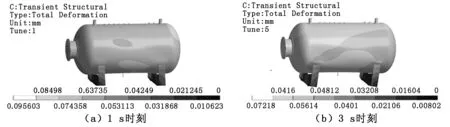
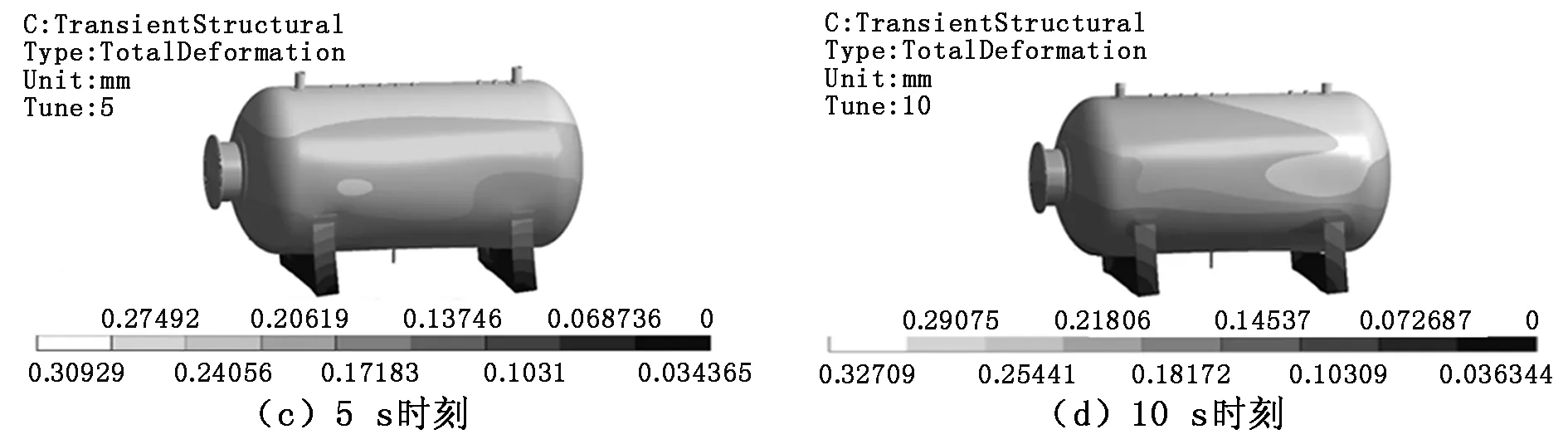
图5 容器壁位移分布图
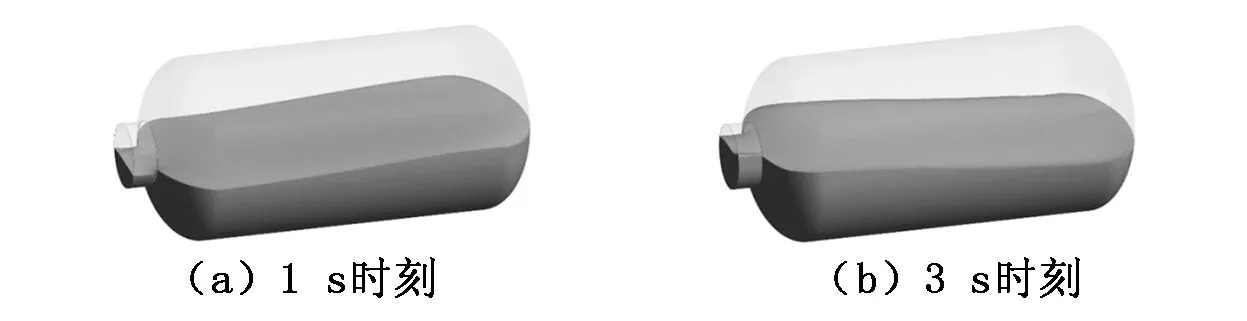

图6 容器内自由液面分布图
2.2 耦合法与附加质量法比较
为了比较本文所用的耦合法和传统的流体附加质量法之间的差异,使用附加质量法重新计算。在容器下半部分内壁面上施加随液体深度变化的质量。
图8为两种方法下的容器筒体部分最大位移时程。由图8可知:附加质量法在地震开始阶段获得的位移量很大,远高于耦合法,耦合法在地震中后期的位移量显著大于附加质量法,由此可以得到液体的晃动将对结构响应产生很大的影响。图9所示的容器筒体最大应力也与位移规律相同。
综上,由于液体晃动所导致的结构响应非常重要,在总体结构响应中为主要因素,因此在分析本问题时,应重点考虑液体的晃动影响。
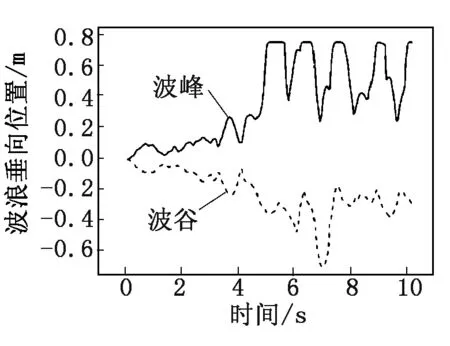
图7 液面波浪高度随时间分布图
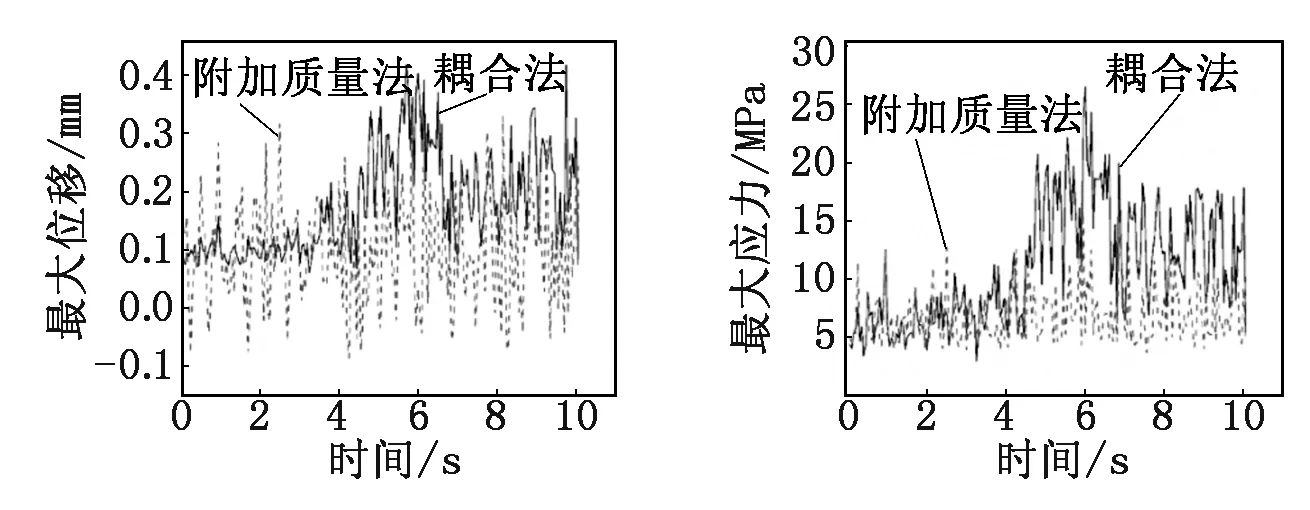
图8 两种方法容器壁最大位移随时间分布图 图9 两种方法容器壁最大应力随时间分布图
3 结论
经过上述分析,最终得到下列关于储罐地震响应分析的结论:
(1) 使用CFD程序来直接对持续震荡流动区域内的气液两相黏性湍流态流体进行计算可以捕捉到液体自由表面的详细动态变化形式,进而通过流固耦合的方式获得其对结构的影响特性。
(2) 在典型地震时程作用下,容器内液体自由表面的“波浪”高度逐渐增大,最终波峰和波谷维持在一定范围内。
(3) 在典型地震时程作用下,容器结构的响应(位移、应力、支反力等)由初始的小幅振动发展为高幅值振动,随着流固相互作用的充分发展,容器响应受液体晃动主导。
(4) 通过与附加质量法比较,判断在本文所研究问题中,液体晃动所导致的结构响应非常重要。在液体和结构的相互作用下,结构响应远大于仅考虑液体的刚性质量的情况,且响应的时域变化也受液体晃动影响巨大。因此在分析相似问题时,应重点考虑液体的晃动影响。
—— 储罐

