数形结合，让学习更轻松

江苏省南通师范第一附属小学 俞乐乐

数形结合在整个小学数学阶段起着很重要的作用。在数学课堂中，教师要发挥学生的主体作用，充分利用学生的形象思维，善于引导学生运用数形结合思想思考、探究问题，让学生对数学知识的理解更加透彻，学习效果更加高效。

一、运用数形结合，活跃学生学习思维

数学学科相较于其他学科，它的知识较为枯燥、无趣，还有些抽象。尤其是一些应用题更是让学生苦恼，很多数学问题会让学生感到题意烦琐，无从下手。而数形结合思想方法恰好能够简化数学内容，利于学生思考。由此，在数学课堂中，教师可以合理地运用数形结合的思想方法，引导学生进一步思考、分析，充分活跃学生的思维。

例如，在教学“简易方程”时，教师在课堂中向学生提出了一个问题：小明的妈妈去超市买了10 千克大米、10 千克面粉、10 千克食用油，一共花费了140 元，其中大米的单价比面粉的单价贵3 元，比食用油的单价便宜2 元，问这三种商品的单价分别是多少？很多学生在读完后题后感到很困惑，不知道该从何处下手。此时，教师引导学生利用数形结合的思想方法来思考这一问题。学生在教师的引导下，假设面粉的单价是x元，并在纸上画出了一条线段表示面粉的单价，再在这一线段的下方画出比它长一点的线段，表示大米的单价，并将其中多出的线段标记上3 元，然后再利用同样的作图法画出了食用油与大米的单价关系。在完成作图后，学生也从中找到了解题的突破口，从第一个图形中得出了大米的单价为（x-3）元，从第二个图形中得出食用油的单价为（x-3+2）元，最后再根据它们的总价钱是140 元，列出相应的方程式，得出最后的结果。

课堂教学中，数形结合思想方法的巧妙运用很好地激活了学生的探究欲望，将数学问题直观化，让学生找到了思考点，有效地促进学生思考、分析，发展了学生的思维。

二、渗入数形结合，促使学生有效思考

数形结合思想的实质是借助数与形之间的转化，将抽象的数学内容变得直观形象，更利于学生学习探究。在数学课堂中，教师可以巧妙地渗入数形结合数学思想，引导学生变抽象为直观，从中更好地发现图形中的数量之间的联系，进而运用并解决数学问题，使得抽象的数学问题迎刃而解。

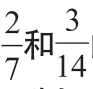
在以上教学案例中，教师从学生角度出发，渗入数形结合思想方法，引导学生将抽象的数学内容转化成形象的图形信息，很好地促进学生融入课堂，实现高效学习。

三、借助数形结合，提升学生学习效率

数学学科中存在很多数学概念比较抽象难懂，如果教师在教学中总是一味地用语言讲解，学生将很难理解，并且只会让学生更加困惑，学习效果不佳。由此，教师需要改变策略，可以从学生的实际出发，引导学生运用数形结合思想分析内容，借助一些具体实物，将抽象概念具体化，让学生能够更好地思考、探究，灵动学生的思维。

例如，在教学“升和毫升”时，教师为了让学生对升和毫升这两个数学概念有更好的认识，从学生的生活选材，在课堂中引入了量筒、试管、水这些物品，并让学生借助这些物品更好地分析、思考。随后，学生在教师的引导下用量筒量取了10 毫升的水，并将这部分水倒在一个试管中感受其体积大小。随后，学生想要知道1 毫升水的体积，于是试着将这10 毫升水均分成10 份，选择其中的一份。学生就这样主动地借助具体实物分析数学内容，从中对数学知识有了很深刻的理解。

数学课堂教学中，教师引导学生借助实物将数学内容直观化、形象化，让学生分析得更加透彻，很好地促进学生的思考，强化学生对所学知识的理解，提升学习效率。

总之，数形结合这一思想方法在数学课堂中起着很重要的作用，它让数学教学不再抽象、烦琐，在很大程度上简化了数学内容，更利于学生思考、内化，让数学学习不再困难。