振幅相位估计法频散分析及校正

王勇

摘   要： 随钻声波测井方法可在地层侵入前测量得到原状地层纵横波速度资料，但测量环境特殊、钻铤占据空间过大，使得声波波形频散严重，传统的时差—时间相关（STC）法失去可靠性。采用基于数据驱动的振幅相位估计法对随钻声波测井资料进行频散分析。为声波波形的幅度和衰减设计高分辨率滤波器，对正演模拟得到的硬地层和软地层环境下单极子、偶极子和四极子声源激发的随钻声波测井响应进行处理，并与加权频谱相干法进行对比。结果表明，振幅相位估计法不需要假定模型参数，而是直接对波形进行处理，分辨率高、抗干扰能力强，为随钻声波测井理论分析及随钻声波测井资料频散校正方法开发提供了理论和方法基础。

关键词： 随钻声波测井;频散分析;振幅相位估计法;数据驱动;加权频谱相干法;正演模拟

引言

随着复杂油气藏、海上深层油气藏的勘探开发日益深化，随钻测井方法的应用越来越广泛。随钻测井方法在地层侵入发生前进行测量，可以最大限度地获取原状地层的信息，在节省钻井时间的同时，能够得到更为精确的地层参数。随钻声波测井作为一种先进的随钻测井方法，在地层弹性参数探测方面体现了非常具有潜力的应用价值。通过随钻声波测井测得的原状地层高精度纵横波速度资料，可以对地层进行更有效的评价，在孔渗特征评价中具有非常重要的作用[1]。此外，随钻声波测井作为一种可以对井外地层进行探测及评价的方法，在地质导向方面也有较大的应用潜力，因为其可以极大提高目的层的钻遇率，避免对其他地层造成伤害，可以有效地提高钻井效率和采油效率。

随钻测井测量环境的特殊性，使得钻铤在井中占据的空间较大，导致在随钻测量模式中测得的声波波形信息与传统的电缆测井差别较大，其中一个突出的特征为频散现象比较严重[2-5]，在某些超低速地层及重泥浆等特殊条件下，四极子波形的频散情况尤为明显。目前，时差—时间相关法（STC法）被普遍地用于阵列声波测井资料的时差提取软件中，可以对地层的纵横波时差进行可靠、有效的提取[6-8]。当声波波形中的某些模式波存在频散时，用STC法处理频散波形得到的速度值通常会低于地层的真实速度值，带来了较大误差，使得后续随钻测井受到了限制。因此，研究随钻声波测井资料的频散分析方法，分析随钻声波测井波形的频散特征并加以校正，对随钻声波测井资料的正确利用至关重要。

现有的声波测井资料频散分析方法有两类：一类是基于理论模型的频散校正方法，一类是纯数据驱动的方法。基于理论模型的方法，理论基础比较简单，但是需要对实际模型进行简化，并作出井眼规则、地层各向同性等假设，通过对比实测值与理论模拟值的差异来分析频散特征，在实际数据处理中受到了较大的限制，这是因为实际声波测井数据中导致频散的因素包括井内流体性质、井壁形狀、仪器是否居中、渗透地层的侵入等，这些均会造成声波波形频散特征的改变[9-10]。纯数据驱动的方法包括加权频谱相干法等，其直接从波形数据特征入手，通过时频分析的手段，处理得到波形的频散特征，在声波测井资料处理中应用比较广泛。

振幅相位估计法是近年来提出的基于数据驱动的高分辨率频散分析新型方法，通过构建幅度、衰减滤波器来实现波形数据的频散分析，在电缆声波测井中显示了较好的应用效果。

本文首先对硬地层、软地层的随钻声波测井数据进行正演模拟，然后采用振幅相位估计法对正演模拟数据进行处理，并与传统的加权频谱相干法的处理结果进行对比。对比发现，振幅相位估计法可以更有效地对随钻声波测井数据进行频散分析，且可以得到更高分辨率的处理结果，为随钻声波测井理论的分析及随钻声波测井资料的频散校正方法开发提供了理论和方法基础。

1  随钻声波测井声场

2  随钻声波测井资料频散分析

振幅相位估计法是一种纯数据驱动的方法，不需要对模型的模式波数量等参数进行假定，直接对数据进行处理即可，具有较高的分辨率。

对于式（19）的振幅表达式，当等于时，在局部空间内为最大值;当的取值为其他值时，。因此，对的局部极值进行搜索，即可判断所处理的波形中存在的模式波的数目。得到振幅数据后，即可在每个频率值处得到对应的慢度值，即频散曲线。

3  结果与讨论

3.1  正演模拟数据频散分析

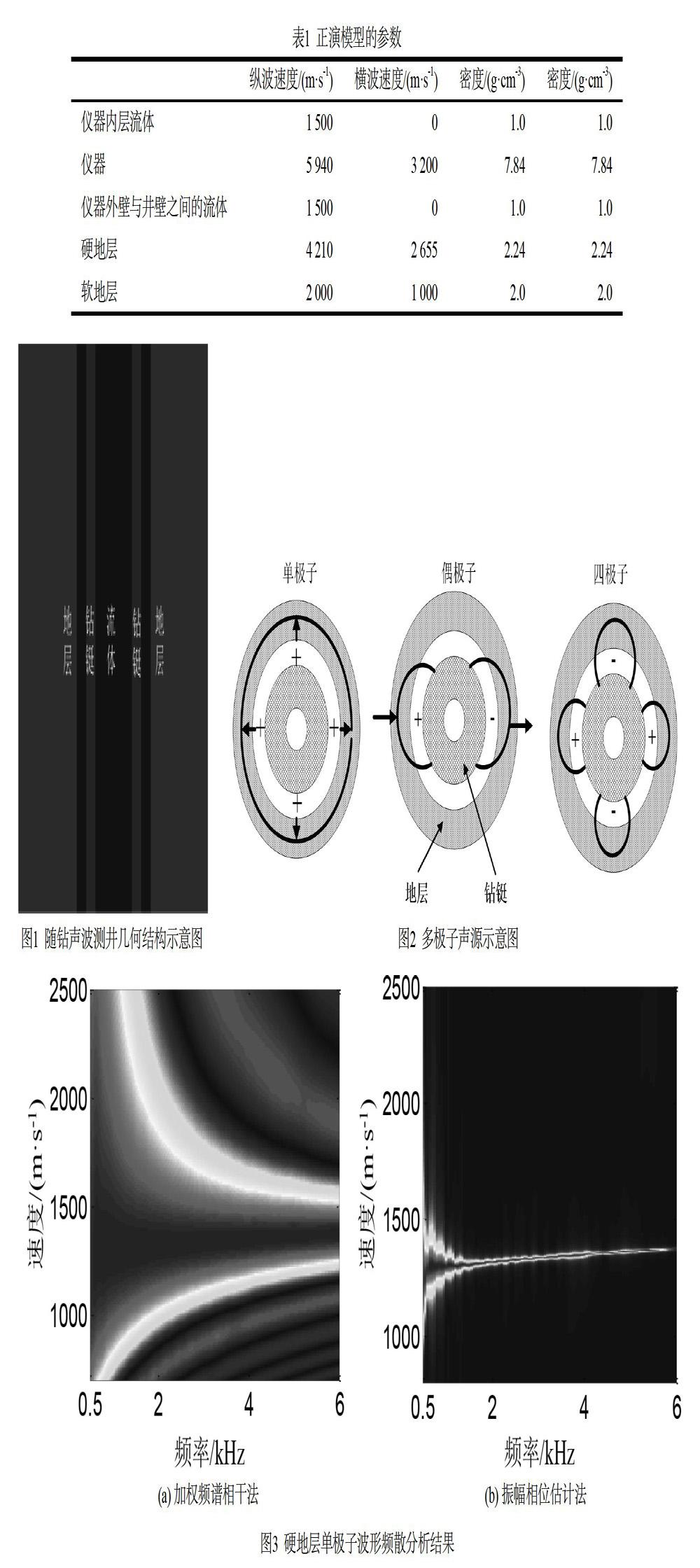
基于第1章的理论，采用正演模拟方法获得硬地层、软地层环境下的随钻声波测井数据，声源类型分为单极子、偶极子和四极子声源三种情况。正演模型的参数如表1所示，此外，仪器的源距为1.37 m，接收器间距为0.152 4 m，时间采样间隔为10 μs，声源主频为4 kHz。随钻声波测井几何结构示意图如图1所示，多极子声源示意图如图2所示。

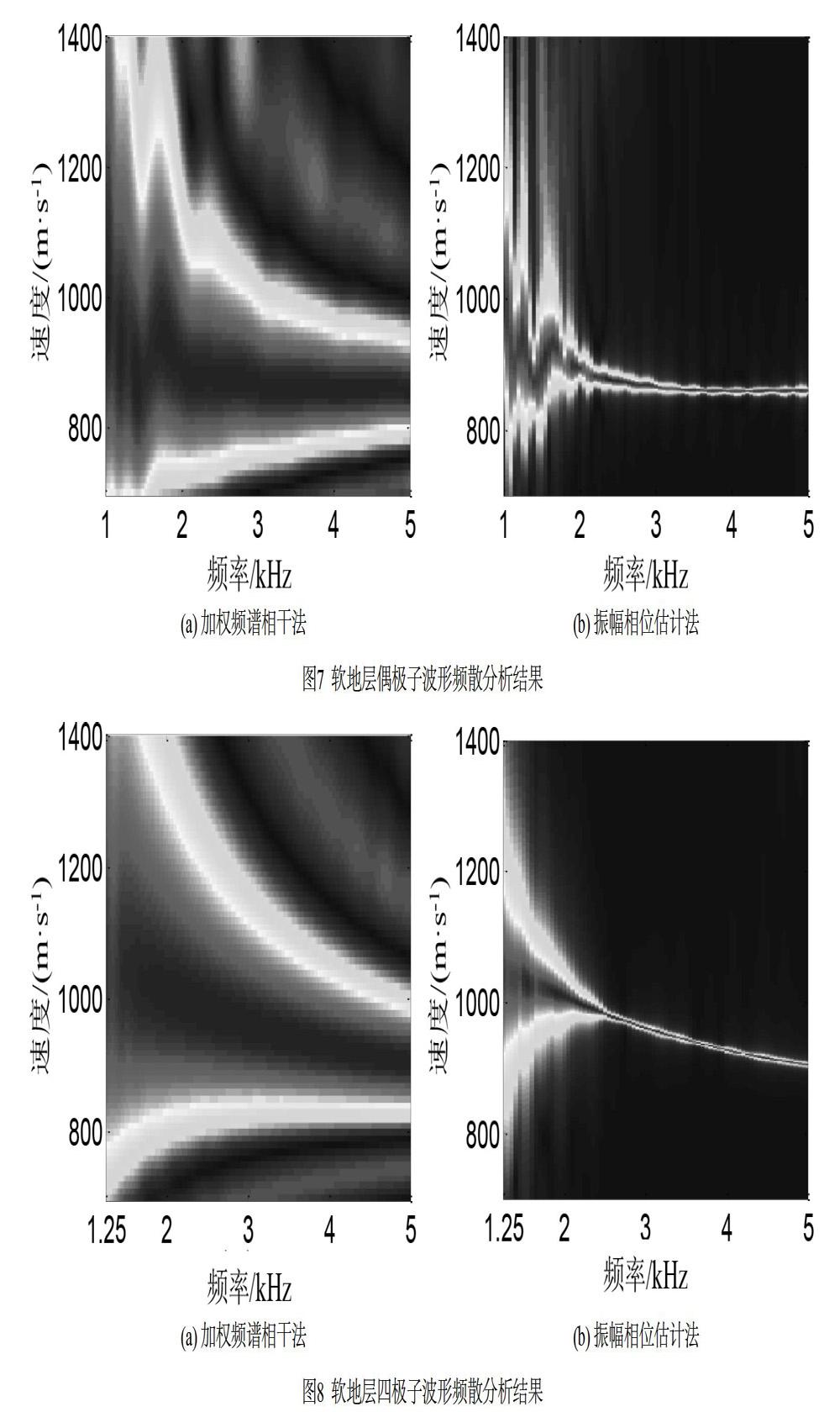
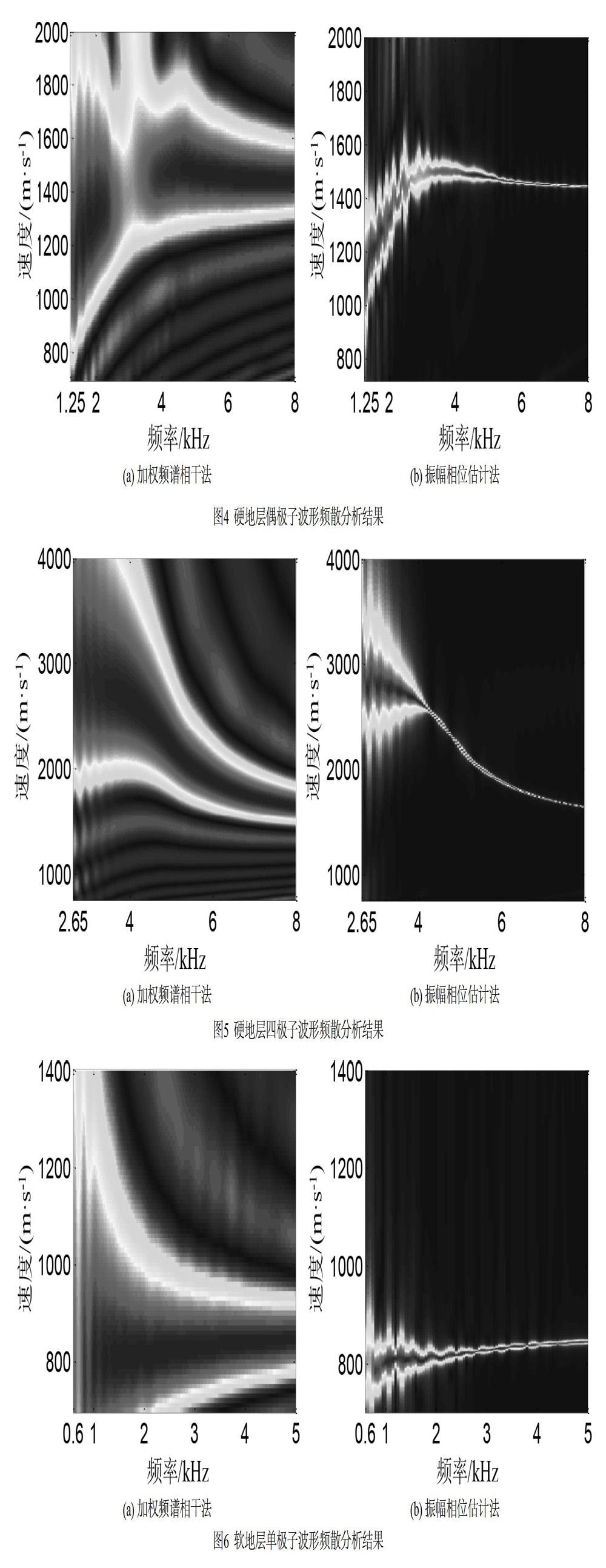
采用表1中的参数进行正演模拟得到波形后，分别用加权频谱相干法、振幅相位估计法计算其频散曲线，结果如图3～图8所示。

3.2  讨论

分析图3～图8的频散分析结果可知，加权频谱相干法和振幅相位估计法都可以对随钻声波测井在硬地层、软地层中测得的阵列声波波形资料进行频散分析。其中，单极子声源激发的井内模式波为斯通利波成分，偶极子声源激发的井内模式波为地层的偶极子波成分，四极子声源激发的井内模式波为地层四极子波成分。在硬地层情形中，受钻铤的影响，地层的偶极子波频散在低频段有干扰，对确定低频截止值处的地层横波速度造成了影响，但在软地层中，地层的偶极子波不受钻铤影响，地层横波速度较为准确。硬地层、软地层情形中的地层四极子波都可以反映地层的横波速度信息，展示了在随钻声波测井环境中，地层四极子波在测量地层横波速度时的优势。此外，虽然加权频谱相干法利用高斯加权方法增加了数据的利用率，但其方法本身的缺陷，导致分析结果的分辨率较低，使频散曲线的提取受到噪声的干扰。相对地，振幅相位估计法采用了高分辨率滤波器算法，在获取幅度信息的同时对慢度信息进行了处理，具有较高的分辨率，在噪声频段也能得到较好的处理效果，不需要进行复杂的处理即可提取得到干净的频散曲线，因此采用振幅相位估计法显然更适合对随钻声波测井资料进行频散分析。

4  结论

本文利用正演模拟方法分别模拟了硬地层和软地层环境下单极子、偶极子和四极子声源激发的随钻声波测井响应，分析了各自的模式波频散特性，同时比选出更准确的频散分析方法。主要结论有：

（1）受复杂的测量环境的影响，随钻声波测井方法测得的阵列波形数据存在频散，采用时间域的STC法无法得到可靠的时差提取结果。通过对比加权频谱相干法、振幅相位估计法两种基于数据驱动方法的结果得出，振幅相位估计法更适合对随钻声波测井资料进行频散分析。

（2）振幅相位估计法通过设计高分辨率的滤波器来实现阵列波形数据中的慢度和衰减的提取，不需要假定模型参数，直接对波形数据进行处理，分辨率高，抗干扰能力强，为随钻声波测井理论分析及随钻声波测井资料频散校正方法开发提供了理论和方法基础。

参考文献

[1] 王华， 陶果， 张绪健. 随钻声波测井研究进展[J]. 测井技术， 2009， 33（3）： 5-7.

[2] Aron J， Chang S K， Dworak R， et al. Sonic compressional measurements while drilling[C]// SPWLA 35th Annual Logging Symposium， 1994.

[3] 測井重点实验室. 测井新技术培训教材[M].  北京： 石油工业出版社， 2003.

[4] 王华， 陶果， 王兵， 等. 多极子随钻声波测井波场模拟与采集模式分析[J]. 地球物理学报， 2009， 52（9）： 2402-2409.

[5] Arian A， Althoff G， Varsamis G L， et al. A new MWD full wave dual mode sonic tool design and case histories[C]//SPWLA 40th Annual Logging Symposium， 1999.

[6] Joyce B， Patterson D， Leggett J， et al. Introduction of a new omni-directional acoustic system for improved real-time LWD sonic logging - Tool design and field test results[C]// SPWLA 42nd Annual Logging Symposium， 2001.

[7] Tang X M， Dubinsky Y，Wang T. Shear-velocity measurement in the logging while drilling environment： modeling and field evaluations[C]//SPWLA 43rd Annual Logging Symposium， 2002.

[8] Minear J， Robbins C. Compressional wave slowness measurement while drilling[C]// SPWLA 36th Annual Logging Symposium， 1995.

[9] Zhan X， Chi Z， Toksoz M N. Simulation of the converted electric field during multipole logging while drilling （LWD）[C]// SEG Technical Program Expanded Abstracts， 2006， 25（1）： 446-450.

[10] Schmitt D P. Shear wave logging in elastic formations[J]. The Journal of the Acoustical Society of America， 1988， 84（6）： 2215-2229.

[11] Haugland S M. Frequency Dispersion Effects on LWD Shear Sonic Measurements in Acoustically Slow Environments[C]// SPE Annual Technical Conference and Exhibition，  2004.