一组艾滋病数据在线性混合效应模型和非线性混合效应模型下的对比

王文琦

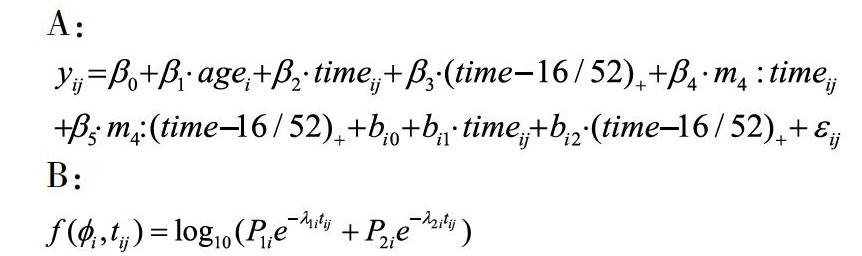
摘 要：本文基于美国艾滋病医疗实验机构ACTG的193A研究中的一组非平衡重复测量数据分别构建了线性混合效应模型和非线性混合效应模型。对长期观测得到的、包含测量误差、缺失值和删失值的复杂艾滋病临床治疗非平衡纵向数据（如CD4，CD8，病毒载量等），实际工作者常用简单的线性混合效应模型替代，从而导致推断精度不能令人满意。本文尝试对一组艾滋病临床治疗中出现的非平衡纵向数据构建非线性混合效应模型，并与实践常用的线性混合效应模型进行比较，希望为此类复杂纵向数据建模实践提供有较好参考价值的建模程序和参考模型。

关键词：线性混合效应模型;非线性混合效应模型;非平衡纵向数据

0 前言

对于非平衡纵向数据的分析，许多工作者一般都用简单的线性混合效应模型进行建模，但是非平衡纵向数据具有删失值，并且大多数非平衡纵向数据是非线性，用简单的线性混合效应模型对其进行建模有一定误差，从而导致推断精度不能令人满意。我们发现非线性混合效应模型能更好地拟合非平衡縱向数据。所以，本文尝试对艾滋病临床数据建立非线性混合效应模型并与线性混合效应模型进行比较。

1 模型理论介绍

线性混合效应模型：在一般的线性模型（线性回归模型、方差分析模型、协方差分析模型等）中假定解释变量固定，即对被解释变量的影响是固定的，不会随个体的变化而变化。但是在多数搜集数据或者进行试验的过程中，我们不能严格控制解释变量，解释变量是从一个总体中随机抽取的一个样本，在这样的情况下，就有必要加入随机效应发展成新的模型来更好地拟合数据，在线性模型中加入随机效应就得到了我们所说的线性混合效应模型。线性混合效应模型的一般形式为：

这里的，假设是独立的，是已知协变量的适当矩阵，表示固定效应的系数和表示特定个体的随机效应。一般来说，的列是的一个子集。响应向量服从以下一个多元正态分布：

其中表示在一些已知的常数下第个个体的次观测值。这里表示是个体数，是个体的观测数。组内误差（）应该是相互独立的均值为零和未知方差为的高斯随机变量。该模型是非线性的，因为g或h是关于的非线性函数。表示未知的种群参数向量。个体矩阵是已知的，向量也表示未知的种群参数，它们不出现在随机效应中。我们假设和是相互独立的。

2 模型的建立与分析

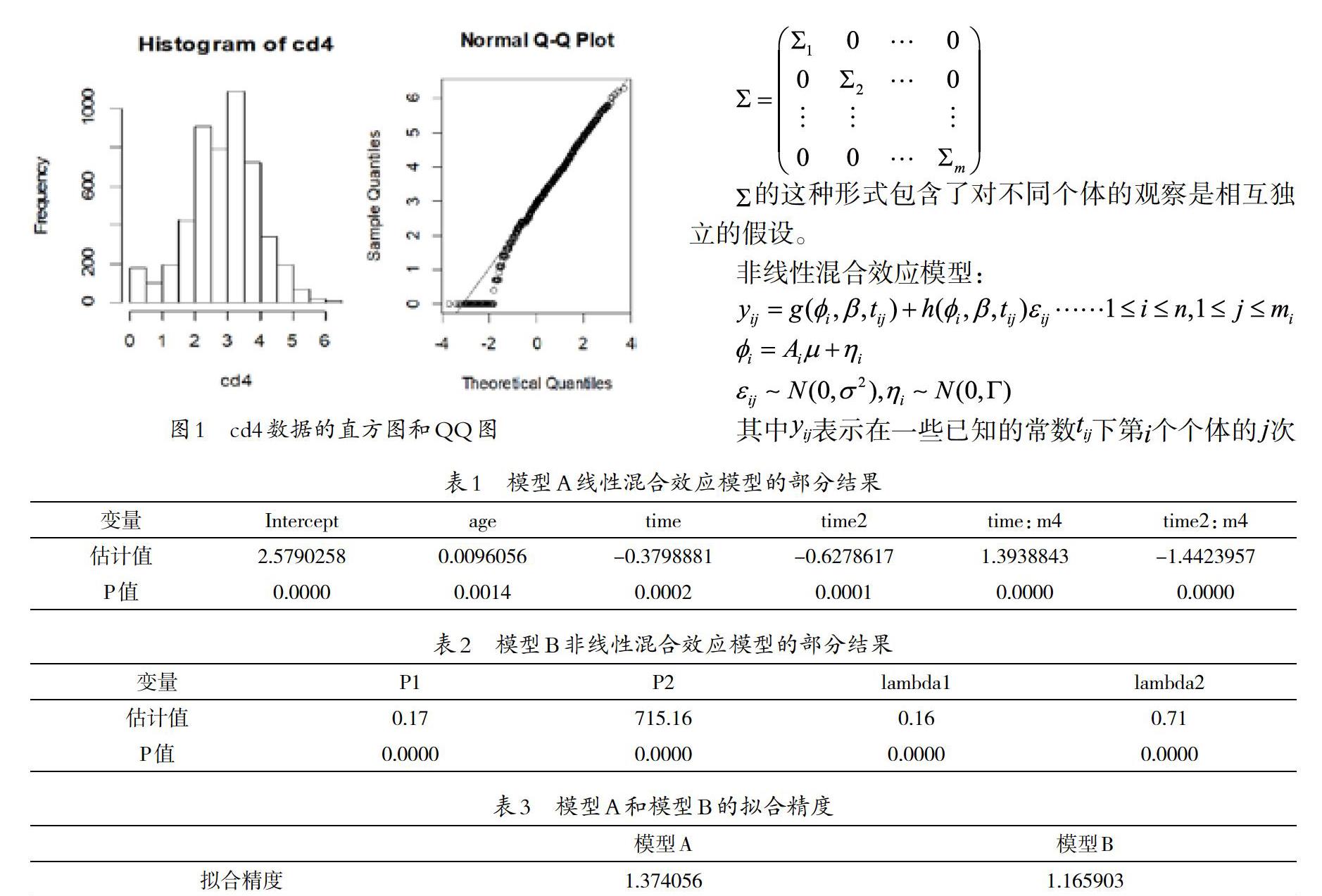
本文运用线性混合效应模型和非线性混合效应模型拟合该组数据。根据线性混合效应模型的基本假设，数据被认为服从正态分布，所以在具体拟合数据时要先进行正态性检验。如果检验结果显示数据不服从正态分布，则要对数据做变换使其近似服从正态分布。

对比两个模型的拟合精度可以发现，模型B优于模型A，总体上非线性混合效应模型比线性混合效应模型拟合该组数据要好。

3 结语

本文用线性混合效应模型和非线性混合效应模型对艾滋病数据进行分析，并对模型的拟合精度进行了比较，发现非线性混合效应模型优于线性混合效应模型。非线性混合效应模型提高了艾滋病数据拟合的精度，得到了更为准确的模型。所以，在实际的数据分析工作中我们要根据数据的特点来选择最优的模型。

参考文献：

[1]L.Wu， A joint model for nonlinear mixed-effffects models with censoring and covariates measured with error， with application to AIDS studies， J. Am. Stat. Assoc. 2002，97：955-964.

[2]L.Wu， Exact and approximate inferences for nonlinear mixed-effffects models with missing covariates， J. Am. Stat. Assoc. 2004，99 ：700-709.

[3]A.Ding，H.Wu，Assessing antiviral potency of anti-HIV therapies in vivo by comparing viral decay rates in viral dynamic models， Biostatistics2001， 2：13-29.

[4]E. Kuhn， M. Lavielle， Maximum likelihood estimation in nonlinear mixed effffects models， Comput. Statist. Data Anal. 2005，49：1020-1038.