在“重构”概念发展的历程中理解本质

陈群娣

[摘 要]理解数学概念的本质是实现有效教学的根本。在“重构”数学发展历程的活动中理解概念本质的“关键要点”：一是在“数学化”的学习过程中构建概念的“组织”;二是在“再创造”的学习活动中理解概念的“本质”。

[关键词]数学发展;过程重构;垂直线段

刘加霞教授指出，实现有效教学的根本在于把握数学概念的本质。可见，小学数学概念的教学，重要的是指导学生理解概念的本质而不是记忆或者背诵概念的形式化定义，换言之，是引导学生经历一个“火热”的数学思考过程，这一学习过程的关键是解决好“3W”问题。一是为什么（Why）：为什么学习这一概念？它在生活中、在数学上有什么用？二是是什么（What）：除了概念的形式化定义外，其数学本质是什么？其来龙去脉是什么？三是怎么样（How）：这个概念与其他概念之间有什么联系？怎样建构“概念图”？那么，如何指导学生理解“三角形的高”这一概念的数学本质？这就必须把握好两个“关键要点”：一是“三角形的高”这一概念的数学本质是什么？是一条垂直线段;二是学生学习这一数学概念，要经历一个怎样的“思维构建”过程呢？换一个角度，教师如何指导学生把“概念发生、发展的历程”和学生构建其“思维之道”相融合，由学生本人把要学的东西自己去发现或创造出来。下面以“三角形的高”教学为例，阐述一下笔者的思考与实践。

【学习过程】

活动一：

师：如下图，从直线外一点A，到这条直线画的4条线段中，哪一条线段最短？为什么？

生1：最短的线段是AC;

生2：从直线外一点到这条直线所画的线段中，垂直线段最短。

【评析】设计“从直线外的点到对边画一条线段，怎样画最短？”这一情境性问题，让学生在问题解决过程中重现“垂直线段”最短这一道理。这是结合学生的现实，以学生已有的知识经验作为数学学习活动的“支架”，为新知的学习“勾画”起学生已有的数学认知结构，为其主动构建新知做好认知准备。

活动二：

师：在三角形ABC中（见图1），有3个顶点，3条边。说一说：每个顶点对应的边是哪一条呢？

生：顶点A对应的边是线段BC;顶点B对应的边是线段AC;顶点C对应的边是线段AB。

师：从顶点A到对边BC画一条最短的线段AD，怎样画呢？

生1：线段AB、线段AC都不是最短的。

生2：垂直线段最短。

师：你们能画出来吗？

生：线段AD是一条垂直线段，最短（见图2）。

师：你是怎样画的？

生1：三角尺的一条直角边与对边BC重合，另一条直角边平移到顶点A，画一条垂线，与对边的交点就是垂足D，这一条垂直线段AD就是点到直线的距离。

生2：我是这样画的，先确定两个端点，其中一个是三角形的顶点A，另一个是从顶点A到对边作一条垂线，交点是垂足D，再把这两个端点用线段连起来。

师：在三角形ABC中，你能从顶点B到对边AC画一条最短的线段BE吗？

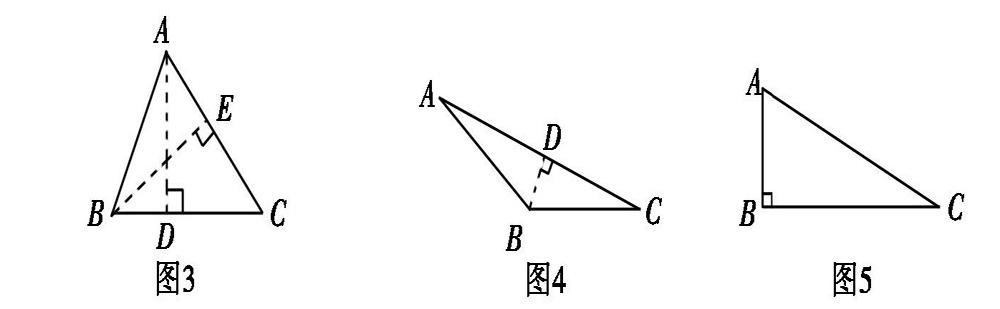
生：线段BE是一条垂直线段，最短（见图3）。

画一画：1.从顶点B到对边AC画一条最短的线段BD（见图4）;2.从顶点A到对边BC画一条最短的线段AB（见图5）。

【评析】根据学生掌握“点到直线的距离最短”这一数学事实，引导学生思考“从一个顶点到对边画一条最短的线段，怎样画才最短？”这一核心问题，让学生在“做数学”的学习活动中，深化对“垂直线段最短”这一数学认知结构的理解。

活动三：

师：什么是三角形的高？（指导学生阅读数学课本）

生1：从三角形的一个顶点到对边作一条垂线，顶点和垂足之间的线段叫作三角形的高。

生2：是一条垂直的线段，其中一个端点是三角形的“一个顶点”，另一个端点是对边的“垂足”。

……

师：说说下图中哪一条是底边上的高？

生1：三角形ABC中（图3），底边AC上的高是BE，底边BC上的高是AD。

生2：三角形ABC中（图4），底边AC上的高是BD。

生3：三角形ABC中（图5），底边AB上的高是BC，底边CB上的高是AB。

   

师：三角形的高有什么共同特点？

生：三角形的“一个顶点”到“对边”的一条垂直线段，這一条线段有两个端点，一个端点是三角形的“顶点”，另一个是顶点对边的“垂足”。

师：三角形可以画几条高？为什么呢？

生1：三角形可以画3条高。

生2：从三角形的一个顶点到对边可画一条高，三角形有3个顶点，最多可画3条高。

师：怎样画三角形的高？

生：一是重合;二是平移;三是找垂足;四是画一条垂直线段。

【评析】让学生在实践、探究活动中构建“高”这一数学概念的形式化定义。教学时，提出“什么是三角形的高？”这一数学问题引领学生阅读课本，感知构成“高”这一数学概念的几个关键“语词”，进一步指导学生个性化地“重构”数学概念的生成过程，与学生已有的数学认知结构“垂直线段”建立逻辑的内在联系，明确构成“高”这一概念的数学结构：一个顶点、对边、垂线和线段。

活动四：

师：我们已经学过了平行四边形和梯形的高这一数学概念。画一画，平行四边形ABCD底边BC上的高？梯形ABCD下底BC上的高？

生1：从平行四边形一条边上的一点A向对边BC画一条垂直线段，线段AE就是底边BC上的高（见图6）。

生2：从梯形平行边上一点A向对边BC画一条垂直线段，线段AE就是下底BC上的高（见图7）。

师：三角形、平行四边形和梯形的底和高有什么相同的地方？

生：是一条垂直线段，这条线段有两个端点，其中一个是“顶点”，另一个是从“一个顶点”到它的对边作一条垂线，这两条线的交点叫“垂足”。

【评析】通过比较，抽象、概括出平行四边形、梯形和三角形的“高”有什么共同的地方，目的在于沟通数学知识之间有逻辑的内在联系，帮助学生形成一个“贯通横纵”的数学概念网络，在数学知识“同化”的学习过程中，理解概念本质，优化学生数学认知结构。

【教学思考】

一、在“数学化”的学习过程中构建概念的“组织”

数学的发生、发展过程就是一个“数学化”的过程。所谓“数学化”，就是数学地组织现实世界的过程。可从两个方面去理解“数学化”，一是“过程”，有“横向”和“纵向”两个方面，横向的数学化是建立数学与生活之间的内在联系，纵向的数学化是数学知识内部的迁移和调整。在教学“三角形的高”这一数学概念时，教师指导学生在解决“从三角形的一个顶点到对边画一条线段，怎样画最短？”这一核心问题过程中，明确“垂直线段”最短的道理，在这基础上，提出“什么是三角形的高？”这一引领性问题，指引学生阅读课本，帮助学生构造出“高”这一概念频繁出现的几个语词：一个顶点、对边、垂线和线段，理解“三角形的高”形式化的定义;二是“组织”，“三角形的高”必须同化到“平行四边形”和“梯形”的高这一数学认知结构中，探究“三角形、平行四边形和梯形的高有什么相同的地方？”这一关键问题，指导学生经历构建数学知识体系的过程。

二、在“再创造”的学习活动中理解概念的“本质”

理解概念的本质是小学数学概念实现有效教学的关键。“三角形的高”这一概念的本质是什么？是一条垂直线段。线段，就涉及线段有两个端点的问题，其中一个是三角形的“一个顶点”，另一个是从三角形的一个顶点到对边作一条垂线，其与对边相交的“一个垂足”;垂直，这就涉及到“相交成直角”的问题。那么，学生应该怎样构建这样的一个数学认知结构呢？荷兰教育家弗赖登塔尔强调：学习数学的唯一正确的方法是实行“再创造”，换言之，学习数学的唯一正确方法就是由学生本人把要学的东西自己去发现和创造出来。这节课，扣紧“三角形的高”的数学本质是“垂直线段”这一判断，设计了如下学习活动：一是在解决“从直线外一点A，到这条直线所画的线段中，最短的是哪一条？”问题的过程中，引导学生明确“垂直线段”最短的数学事实，回顾与反思“两条直线互相垂直”关键所在是把握“两条直线相交成直角”这一基本活动经验;二是出示三种不同类型的三角形“直角三角形”“钝角三角形”“锐角三角形”，引导学生运用已有的知识经验，解决“点到直线的距离最短”这一数学问题，“垂直线段”这一“数学结构”刻画在学生的认知结构中;三是提出“什么是三角形的高？”这一问题，指引学生阅读课本，在“垂直线段”这一认知结构的基础上，帮助学生明晰“三角形的高”形式化定义几个关键语词：一个顶点、对边、垂线和线段，这一数学结构烙印在学生的认知结构中;四是通过比较平行四边形、梯形和三角形的“高”有什么共同的地方？幫助学生把“三角形的高”这一“认知结构”同化到“平行四边形”“梯形”的高这一“模型”中，建立数学知识之间纵向联系的纽带，优化学生的认知结构。

[参 考 文 献]

[1]刘加霞.小学数学有效教学[M].北京：北京师范大学出版社，2015.

[2]蓝艺明.深度体验小学数学概念教学的积极追求——“三角形的认识”教学思考与实践[J].教育科学论坛，2017（12）.

[3]郭庶，王瑞霖.弗莱登塔尔再创造理论对数学教学提出的挑战[J].首都师范大学学报（自然科学版），2015（5）.

[4]郑玮，郑毓信.HPM与数学教学中的“再创造”[J].数学教育学报，2013（3）.

（责任编辑：李雪虹）