铁路路基动态变形模量的数值模拟分析

魏瑶 夏琼 王旭

（兰州交通大学土木工程学院，兰州 730070）

铁路路基压实质量是保持线路稳定与平顺，保证列车高速、安全运行的重要条件，关系到整个工程的施工进度、质量等。科学合理的路基检测方法是路基施工质量的重要保证。路基的压实质量主要通过控制填料的密实度指标和强度指标来实现。目前铁路路基质量检测指标主要有压实系数K、地基系数K30、7 d 饱和无侧限抗压强度和动态变形模量Evd，其中Evd主要是用于检测高速铁路和重载铁中的路基基床部位，反映在高速或重载列车动荷载作用下路基基床抵抗动变形的能力。TB 10621—2014《高速铁路设计规范》和TB 10625—2017《重载铁路设计规范》分别规定高速铁路、重载铁路基床部位压实质量检测均包含Evd指标，TB 10623—2014《城际铁路设计规范》规定城际铁路无砟轨道基床部位也包含Evd指标。

我国在1999 年开始对Evd检测方法进行立项研究。Evd的检测方法于2004 年正式写入TB 10102—2010《铁路工程土工试验规程》，引用了当时部分相关研究成果。黄大维等［1］通过兰新铁路第二双线路基试验段戈壁填料现场填筑试验，运用三维动态有限元数值分析并结合现场检测结果，对Evd值的影响因素进行了分析。常丹等［2］通过有限元分析，运用线性回归的方法得出了K30与Ev2，K30与Evd的线性关系表达式及线性相关系数。但对Evd进行测试时，冲击荷载作用下承载板与土体的接触压力、Evd测试结果的影响因素、有效测试深度等还需要进一步研究。

本文从弹性静力学理论出发，在一定的假设条件下推导Evd的理论计算公式；利用有限元数值方法模拟动态变形模量测试仪的工作原理，考虑落锤冲击荷载及被检测土体的弹塑性本构关系；分析承载板与土体接触压力、承载板下土体内竖向动应力衰减规律及竖向动位移发展规律等；进一步研究Evd测试结果的影响因素、有效测试深度等，从而为合理进行Evd试验提供依据，为今后的铁路路基压实质量检测提供参考。

1 动态变形模量Evd理论公式

动态变形模量测试仪由加载装置、荷载板和沉陷测定仪3部分组成。其工作原理主要是利用落锤从一定高度自由下落在弹簧阻尼装置上，产生的瞬间冲击荷载通过弹簧阻尼装置及传力系统传递给φ300 mm的承载板，在测试面产生与土体工作条件相符的动应力，使承载板发生沉陷，该沉陷幅值由沉陷测定仪采集记录［3］。

Evd虽然是反映动荷载下土体抵抗变形的指标，但由于落锤对路基表面施加动荷载时，落锤对路基的作用时间非常短，一般情况下不超过25 ms，路基还未出现塑性变形，荷载就已经卸除。所以，可以认为在落锤的冲击下路基主要产生了弹性变形［4］。Evd的理论计算公式是基于弹性力学理论推导得出的［5-6］。半无限空间弹性体表面放置圆形刚性承载板，在其中心作用竖向荷载P时，板中心下不同深度处土体竖向附加应力σz、竖向位移s理论计算公式分别为

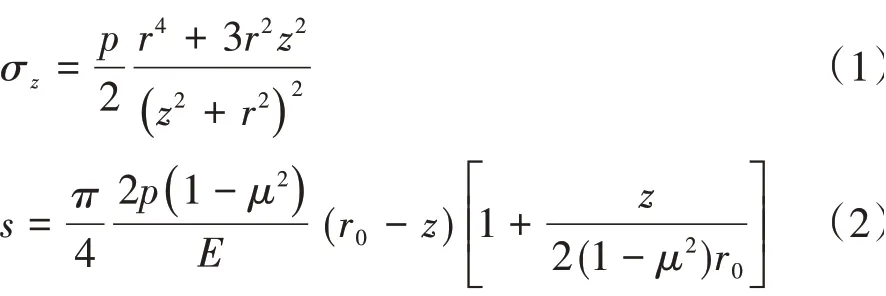
式中：p为等效均布荷载集度，p=P/πr2；r为圆形载荷板半径；z为深度；μ为土体的泊松比；r0为计算点到作用点的距离

动态变形模量理论计算公式是根据承载板底面接触压力和位移的峰值计算地表面z=0 处的接触压力、位移。将z=0 分别代入式（1）、式（2）即可得到圆形刚性载荷板中心点下接触压力σ及Evd的理论公式分别为

将μ= 0.21 代入式（4），可以得到动态变形模量Evd的常用计算公式为

式（5）正是TB 10102—2010 给出的动态变形模量Evd计算公式34.0.7—1。不同的是该规程对p解释为承载板下的最大动应力并标定为0.1 MPa。通过以上的分析可知，式（5）中的p（即TB 10102—2010 式34.0.7—1 中的σ）并不是承载板下的最大动应力，而是承载板下等效均布荷载计算值，式（3）表明p值是承载板下最大动应力的2倍。如果用承载板下的最大动应力来计算Evd，则应该按式（6）计算。

TB 10102—2010 中Evd试验采用的测试仪最大冲击力为7.07 kN，圆形承载板的直径为300 mm，计算得到承载板下等效均布荷载p= 0.1 MPa，代入式（5）可得出

式（7）正是TB 10102—2010 中Evd简化计算式34.0.7—2。可见，TB 10102—2010 对Evd计算公式中的σ解释欠准确，但其数值是按理论公式（5）中p来取值，故TB 10102—2010中Evd简化公式34.0.7—2与式（7）相同。

2 动态变形模量Evd有限元模拟分析

2.1 有限元模型

根据Evd试验过程，用MIDASGTS 有限元软件来模拟分析土体Evd的测试结果，建立土体有限元模型如图1 所示。为了减小边界效应，模型尺寸定为3 m ×3 m×3 m 的正方体土体模型，选用Drucker-Prager 本构模型模拟其弹塑性力学性质。模型的边界条件侧面为黏性边界［7］，底部采用固定约束。承载板选用圆形钢板，采用弹性本构模型，钢板直径为30 cm、厚度为2 cm。土体及钢板的材料参数见表1。

图1 有限元模型

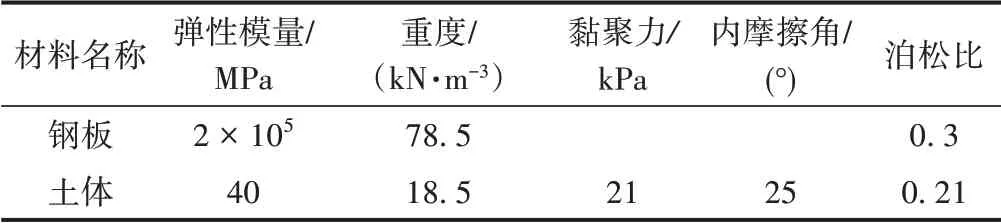
表1 材料参数

钢板周围进行网格划分的大小为0.03 m，模型边缘尺寸为0.1 m。钢板附近网格划分越来越密，这可使钢板影响范围内的计算更准确。

根据动态变形模量测试仪的作用原理，作用在圆形刚性承载板上的竖向荷载P为冲击荷载。根据动态变形模量测试仪标定情况可得，当冲击时间为4 ms时，冲击力达到最大值7.07 kN，荷载脉冲宽度为18 ms，参照文献［2，8］确定冲击动荷载时程曲线，见图2。

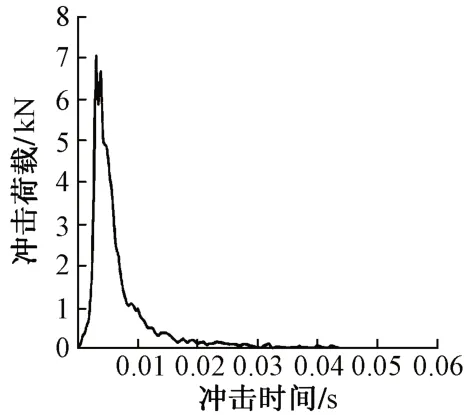
图2 冲击荷载时程曲线

2.2 承载板下接触压力分析

在一定的假设前提下推导的圆形刚性板作用中心竖向荷载P时，板下接触压力p(r)即在弹性半无限空间下且没有考虑土体的性质对接触压力的影响［9-10］，见式（8）。实际的土体一般是非线性材料，且在Evd测试时承载板上作用冲击荷载，此时承载板下接触压力与理论公式（8）计算值不一定相等。

式中，a为距承载板中心处的距离。

在冲击荷载作用下，承载板下接触压力也是随时间变化的，以承载板中心点为例，接触压力时程曲线见图3。可知，接触压力在4 ms时达到幅值，与冲击荷载幅值对应的时间是一致。以下的分析均取接触压力的幅值。

图3 承载板下中心处位移时程曲线

承载板下接触压力沿荷载直径的分布见图4。对比理论计算值和数值模拟结果可知，理论计算与数值模拟的接触压力分布形状相似，沿承载板直径方向变化趋势是一样的。承载板中心附近接触压力最小，越往承载板边缘接触压力越大，理论计算承载板边缘处的接触压力是趋于＋∞，这与实际是不相符的。在沉降发生之前，边缘应力已经使土体屈服而导致压力重分布，结果使得中央小而边缘逐渐增大［11］。接触压力理论计算值与数值模拟结果在承载板中心点附近差别较明显，以土体动弹性模量Ed=40 MPa 为例，以中心点为圆心半径0.09 m 范围内数值模拟结果较理论计算值要大，中心点理论计算值为50 kPa，数值模拟结果为62.53 kPa，较理论计算值大20.04%。

图4 接触压力沿荷载板直径的分布

分析两者差异原因可能是：理论计算公式是在静力作用下通过弹性力学的理论推导出来的；数值模拟中土体按弹塑性材料考虑，在圆形刚性承载板上作用竖向冲击荷载，图4 中基底接触压力在圆形刚性承载板中心处有小的突起，可能是由于应力波在中心处交汇处所产生的［12-13］。由图4 可知，不同的动弹性模量下接触压力沿荷载板直径的分布基本上没有变化，可以忽略土体动弹性模量对接触压力的影响。

2.3 土体表面动位移分布规律

在冲击荷载P作用圆形钢板的整个过程中，承载板中心处土体表面竖向位移与时间的变化关系见图5。

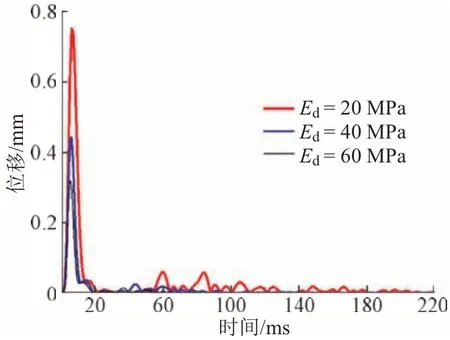
图5 承载板中心处土体表面竖向位移时程曲线

由图5 可知：承载板中心土体表面的竖向位移在4 ms时达到幅值，在冲击荷载结束时即18 ms降低至0附近，之后随时间还产生微小波动直至220 ms。在动态变形模量测试仪产生的冲击荷载下，土体产生的是弹性变形，最终可以完全恢复至0。不同的土体动弹性模量下，承载板中心土体表面位移时程曲线幅值差别明显，即随着土体的动弹性模量增大，荷载板中心处的位移逐渐减小，达到幅值的时间基本一致；冲击荷载结束后位移的小幅值波动略有差别，动弹性模量较小时的波动幅值较大，且响应时间会更长。当Ed=20 MPa 时，位移的响应时间大约为220 ms；当Ed=40 MPa 和Ed=60 MPa，位移的响应时间大约为150 ms。

位移响应时间差异的原因是冲击荷载作用下土中形成一脉冲波，土体有明显的位移波形，不同的动弹性模量下土体的位移回弹次数也不一样。动弹性模量越小，土体的位移回弹现象越明显。这是由于在冲击荷载下土体动弹性模量越小其内部受到的扰动越明显［14-15］。

2.4 动态变形模量的影响因素

2.4.1 动弹性模量Ed

在土体的其他参数不变的条件下，动弹性模量分别取10，20，30，40，50，60 MPa进行动态变形模量模拟分析，模拟结果见表2。表2 中Evd模拟值是利用荷载板中心下最大动应力、土体表面位移按式（6）计算的，Evd计算值是利用土体表面位移按式（7）计算的。

对表2中数值进行拟合计算，可知：在不同的动弹性模量下，Evd与Ed之间是一种近似的线性关系，模拟值和计算值的相关系数分别为0.99，0.98，说明Evd和Ed之间存在着很好的线性关系，Evd作为检验路基压实质量标准与Ed具有相似的力学意义。数值模拟结果总体较理论计算结果大，这是因为两者计算所用的土体表面动应力幅值不一样。前面分析已显示数值模拟得到的土体表面动应力幅值较理论计算值大；当动弹性模量变化范围较小的时候，数值模拟结果与理论计算结果的差别较小；随着动弹性模量的增大，数值模拟结果与理论计算结果相差越来越明显。

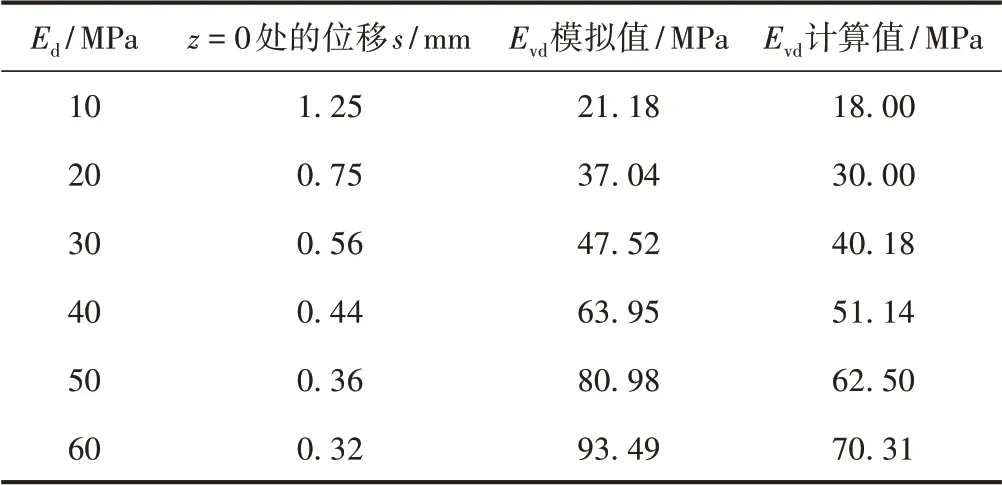
表2 不同Ed时Evd结果

2.4.2 土体泊松比μ

其他参数不变，泊松比分别取0.10，0.21，0.30，0.40 来模拟分析土体（Ed=40 MPa）动态变形模量，计算结果见表3。

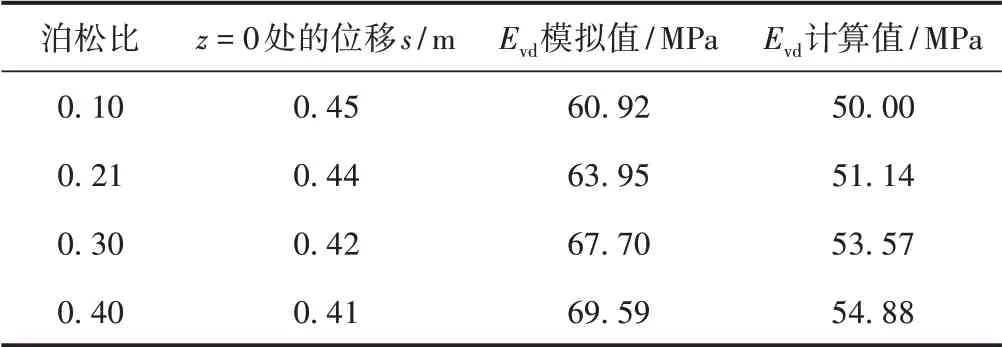
表3 不同泊松比时Evd的计算结果

由表3可知：随着土体泊松比μ增大，Evd总体呈逐渐增大的趋势，但泊松比对Evd的影响不是很明显，泊松 比 由0.1 增 加 至0.4，Evd由60.92 MPa 增 加 至69.59 MPa。如果不考虑泊松比按式（7）（对应μ=0.21）计算Evd，当μ=0.1，μ=0.3，μ=0.4 时计算结果误差分别仅为4.74%，5.86%，8.82%。这说明不考虑土体泊松比的影响，按式（7）Evd所导致的误差可以忽略。

2.5 Evd的有效测试深度

2.5.1 按承载板中心土体竖向位移确定

TB 10102—2010 中规定竖向位移衰减70%～80%对应的深度为动态变形模量的有效测试深度。根据数值模拟结果计算，得出承载板中心处土体的沉降衰减达到70% ～80%对应的深度约为0.5～0.7 m（Ed=40 MPa，μ=0.21），见表4。

表4 承载板下竖向位移衰减百分比

2.5.2 按承载板中心竖向附加应力确定

冲击荷载作用下，承载板中心土体的竖向附加应力在z=0.1 m 处达到最大值，z在0～0.1 m 内，附加应力随深度的增加而增加，当z ＞0.1 m 时，附加应力逐渐减小。根据数值模拟的结果计算，得出承载板中心处土体的竖向附加应力衰减达到70% ～80%对应的深度约为0.5～0.6 m（Ed=40 MPa，μ=0.21），见表5。

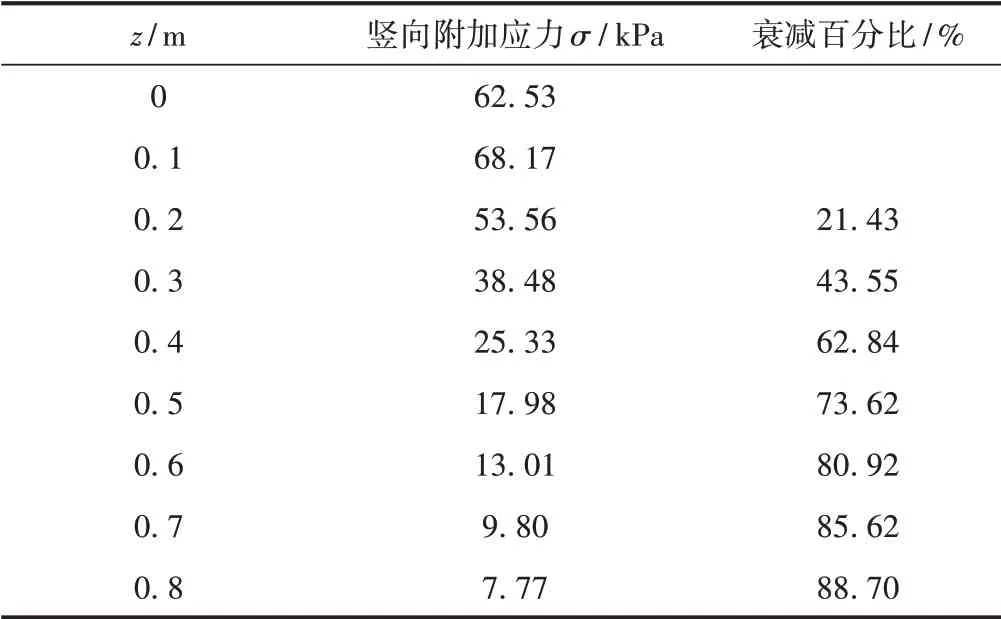
表5 荷载板下竖向附加应力衰减百分比

综合考虑按竖向位移和竖向附加应力衰减确定的有效测试深度［16-17］，建议动态变形模量测试仪的有效测试深度取0.5～0.6 m。

3 结论

1）承载板下接触压力模拟结果与理论值整体变化规律相似，在承载板中心一定范围内，模拟结果较理论计算值大；土体动弹性模量对接触压力影响较小，计算时可忽略其影响。

2）在动态变形模量测试冲击荷载作用下，承载板中心土体表面的竖向动位移在4 ms时达到幅值，在冲击荷载结束时即18 ms 降低至0 附近，之后随时间在0附近产生微小波动，经过一段时间后最终板中心位移恢复至0，说明土体没有产生累积塑性变形，且波动时间与动弹性模量有关。

3）动态变形模量Evd与土体动弹性模量Ed呈显著的线性相关关系，Evd数值模拟结果较理论计算值大，且动弹性模量越大两者差别越明显。

4）土体泊松比对动态变形模量影响并不明显，按μ=0.21来计算动态变形模量，误差可以忽略。

5）按承载板中心土体竖向位移、竖向附加应力衰减70%～80%两种方法分析动态变形模量有效测试深度，建议有效测试深度取0.5～0.6 m。