一道标准学术能力测试题的探究与反思*

陈凌燕

(福建省仙游金石中学，351200)

由清华大学自2017年发起的“中学生标准学术能力测试(THUSSAT)”几经发展,因其命题质量不断提升,受到越来越多师生的关注.2019年THUSSAT11月诊断性测试卷中一道立体几何模块求线面夹角的试题,其计算量、思维容量都不小,引起笔者的思考,现整理成文与同仁分享,以期抛砖引玉.

一、原题呈现

题目在菱形ABCD中,∠ABC=60°,E、F分别是边AB、CD的中点,现将∆ABC沿着对角线AC翻折,则直线EF与平面ACD所成角的正切值最大值为( )

二、思路分析及解题过程

本题以菱形的翻折为载体,考查直线与平面所成角的概念与计算等基础知识,考查学生空间想象能力、运算求解能力、推理论证能力以及数形结合、函数与方程思想,考查数学运算、直观想象及逻辑推理等核心素养.

思路1几何法

由线面夹角的定义入手,先作出直线与平面所成角,再通过几何法求解.

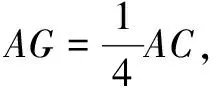
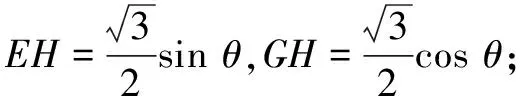
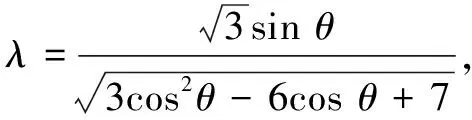
思路2坐标法

建立空间直角坐标系,用向量法求解.

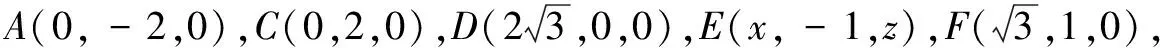
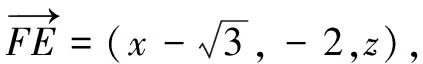
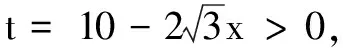
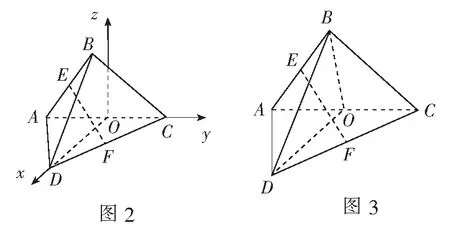
思路3基底法

避开建立空间直角坐标系,还可以利用向量基底法求解.

解法3如图3，取AC的中点O,易知∠BOD为二面角B-AC-D的平面角.

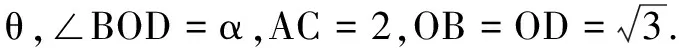
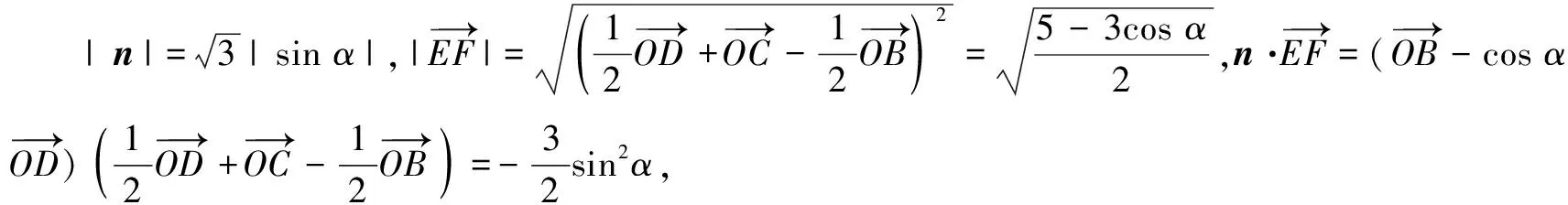
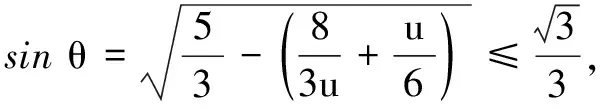
三、反思感悟

1.规避特殊,服务选材

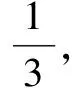
2.知识交汇,强化综合

作为立体几何模块试题,本题蕴含了函数与方程、三角及基本不等式等多个模块的知识,这与近年来的全国卷高考题的命题趋势一致,例如2019年全国课标I卷理科21题就是概率统计与数列交汇的问题.多个知识点交汇,能考查学生能否避开单一知识点的解题套路,将所学知识融汇贯通,在遇到问题时能应用所学予以分析解决.

3.多维探究,激活思维

对立体几何问题,学生解题时常常存在思维定势,通常习惯于建立空间直角坐标系求解,不能适时运用几何法、向量基底法的优势寻求问题的简便解法.因此，需要我们在综合训练教学中引导学生活化思维的深度和广度,以全方位提升核心素养.