用奔驰定理与极化公式巧解向量题

龚 勤

(湖南省岳阳市第一中学 ，414000)

“奔驰定理”与“极化公式”是平面向量中两个最优美的结论.“奔驰定理”是有关三角形四心向量式的完美统一表示，尤其在解决与三角形的四心相关的问题时有着决定性的基石作用;涉及数量积的取值范围或最值时，利用“极化公式”可将多变量问题，转变为单变量问题，再用数形结合等方法求解.本文略举数例说明两者的应用.

一、奔驰定理及其应用

结论1(奔驰定理) 已知O是∆ABC所在平面内的一点,∆BOC、∆AOC、∆AOB的面积分别为SA、SB、SC,则

该结果中结论的形式非常优美, 且其基本图形和奔驰的Logo很相似，因此我们把它称为奔驰定理.由奔驰定理及平面向量基本定理,不难得到如下推论

思路5综合法

综上，|2lnx-ln 7|>2|2lnf(x)-ln 7|.由an>0,得|2lna1-ln 7|>2|2lna2-ln 7|>4|2lna3-ln 7|>…>2n-1|2lnan-ln 7|.

因为a1=1,ln 7<2,所以2n-2|2lnan-ln 7|<1成立.

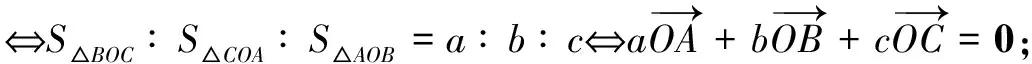
证明这里仅对(4)给出证明过程

同理可得S∆COA∶S∆AOB=tanB∶tanC,S∆BOC∶S∆AOB=tanA∶tanC,所以S∆BOC∶S∆COA∶S∆AOB=tanA∶tanB∶tanC.

(A)2 (B)3 (C)4 (D) 5

二、极化公式及其应用

在初中平面几何中,有一个重要性质:“平行四边形的对角线的平方和等于相邻两边平方和的两倍.”该性质用向量法很容易证明,具体过程如下.

(a+b)2=a2+2a·b+b2,

①

(a-b)2=a2-2a·b+b2,

②

①+② 可得AC2+BD2=2(AB2+AD2)，得证.

从向量的角度来研究平行四边形,由上述① 、② 两式相减,可得平行四边形的如下另一个重要性质.

③

③ 式通常称为极化公式的平行四边形模式.如图3,设点M为ABCD对角线的交点,则由AC=2AM,可得极化公式的如下变式——三角形模式.

推论如图4,设点M为∆ABD的边BD的中点,则有

④

(A)2 (B)3 (C)6 (D)8

数学之美就美在它的千变万化,一道好题,一种巧解，一丝联系，一点变化都可能给你的解答带来简便,带来美的享受.