一道数列不等式模考题的多角度求解

苏 悦

(山东省泰安市宁阳县第一中学，271400)

(1)求a;

(2)讨论g(x)=x(f(x))2的单调性;

(3)设a1=1,an+1=f(an),证明不等式2n-2|2lnan-ln 7|<1恒成立.

本题是2020年山东省模考第22题.第(1)问和第(2)问较为基础,学生较易得分，易知a=7,具体过程从略.第(3)问主要考查数列、函数和不等式的综合应用,利用分析法进行推理,考查数列的递推公式、数列型不等式放缩以及构造函数证明,难度非常大．其难点有两个：一是所证数列不等式的放缩转化，二是去绝对值符号．这里，笔者以去绝对值符号为突破口，总结了五种解法供大家参考．

思路1利用对数性质去绝对值符号

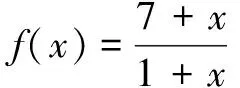
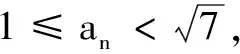
思路2平方法去绝对值符号

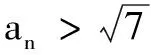
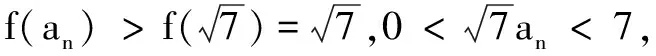
综上，2n-2|2lnan-ln 7|<1成立.

思路3作差法去绝对值符号

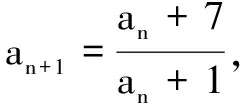
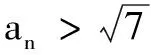
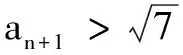
综上，2n-2|2lnan-ln 7|<1成立.

思路4奇偶项去绝对值符号

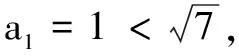
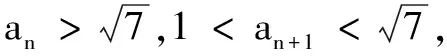
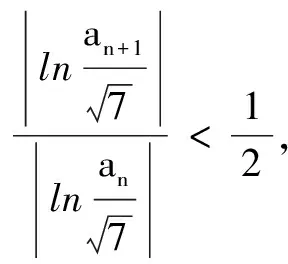
所以2n-2|2lnan-ln 7|<1成立.