基于模型模拟的森林穿透雨收集装置的优化设计及分布

李 淳

(1.辽宁省森林经营研究所，辽宁 丹东 118002；2.辽宁辽东半岛森林生态系统国家定位观测研究站，辽宁 丹东 118002)

森林具有降雨再分配功能，对森林的水循环起到重要的影响，森林与水分的相互作用关系是当今森林生态学研究领域的核心问题之一[1]。林冠截留和穿透雨是研究降雨再分配的重要环节，已有很多相关的研究[2-7]。关于树冠截留的研究，从模型角度可分为经验模型、半经验半理论模型和理论模型[8]。在半经验半理论模型和理论模型中，很多学者从各影响因素角度和过程对树冠截留进行了分析和模拟[9-12]，可将这些影响因素统称为树冠对降雨的拦截能力。在实际观测过程中，树冠截留量无法直接观测获得，因此如何获取准确的穿透雨数据成为研究森林降雨再分配功能的关键。结合实际工作经验，设计理想模型，对理想穿透雨模型进行研究，可提高穿透雨数据的精度，为森林水文过程深入研究提供理论依据。

1 理论模型

1.1 模型基础假设

林内降雨再分配可分为3个阶段，第一阶段，枝叶未达到饱和，大气降雨只能穿过林冠层缝隙到达地面，树冠下各处穿透雨量小于森林降雨量；第二阶段，枝叶逐渐达到饱和，饱和的枝叶不再具备拦截能力，将大气降雨汇聚后形成二次降雨，林冠下部分区域穿透雨量逐渐增大；第三阶段，林冠层达到饱和，树冠各处的拦截能力不再变化，林冠层对大气降雨起到分流和汇聚的作用，受汇聚作用影响，部分区域穿透雨量大于森林降雨量[3，7，13-14]。单株树冠的拦截能力受树种、树型、枝干夹角、叶面积指数、树冠厚度等参数影响[3，7，11-16]，林内任意区域林冠的拦截能力同时与该区域植被的空间分布相关。

为突出研究穿透雨收集装置的形状和设置方式问题的针对性，对模型进行简化。忽略林木单体差别，统一树种、树型、树干等因素对穿透雨的影响，将树冠假设成圆锥形，忽略树干径流量，将所有树冠截留的影响因素转换到树冠厚度中，即任意空间位置正上方树冠的拦截能力与该处正上方树冠厚度成正相关关系，设树冠拦截系数为f(δ)。模型中各处树冠对降雨的拦截系数不变，即f(δ)固定不变。将林地视为是无限广阔、理想均一的林分模型(图1)。因为结构均一，所以区域OACB是最小无重复林分结构分布单元，整个林分由OACB重复拼接构成。区域OFDE为最小无重复穿透雨分布分析单元，OFDE的结论可代表整个理论林分模型。设单株树冠冠幅半径R，林冠层厚度H，林木株间距G。

1.2 分析方法

将收集装置中心点作为基准参照点，将各种形状、大小的收集装置放置在最小无重复计算分析单元OFDE的范围内。根据收集装置区域穿透雨量和OFDE区域穿透雨量的比值k(即观测值与真实值的比)，判断该点是否为合理放置位置。根据合理设置位置范围的大小，判断出最佳穿透雨收集装置形状、大小和放置方式。模型中，设定当k值在[0.95，1.05]区间内时，该点为合理放置位置。

图1 理论模型的最小无重复计算单元

2 函数方程推导及分析

2.1 函数方程推导

根据模型假设条件，当大气降雨量Ra固定时，OFDE区域的穿透雨量Rt为固定常数，所以只需推导出收集装置区域树冠截留量的计算方程，即可计算k值，对模型进行分析。

各处降雨量、截留量、穿透雨量(mm)等于相对应降雨体积量除以相对应区域面积。设Var为OFDE区域大气降雨体积量；Vsr为OFDE区域树冠截留体积量；Vtr为OFDE区域穿透雨的体积量；Ra为OFDE区域大气降雨量(mm)；Rs为OFDE区域树冠截留量(mm)，S为OFDE区域面积。设OFDE区域林冠层体积Vl与该区域大气降雨体积量比为α，公式：

α=Vl/Var

树冠截留系数：f(δ)=Visr/Vis

则RΔs=RΔa·f(δ)·α·VΔs/VΔl

(1)

式中：RΔa、f(δ)、α均为常数。结合(1)式可以看出，任意区域内树冠截留量RΔs与该区域大气降雨量RΔa比值的研究，可转化为对该区域树冠体积VΔs与该区域林冠层体积VΔl比的研究。根据(1)式和二重积分体积求导方法，建立任意区域正上方树冠体积求导方程，

(2)

注：φ1(x)，φ2(x)，φ3(y)，φ4(y)为任意区域的水平面值域函数；f(x，y)表示局部区域的树冠hi的函数。

当该任意区域SΔ为穿透雨收集装置区域Sf时，收集装置区域树冠截留体积量等于该区域树冠截留体积量，即Vfsr=VΔsr。由(3)式求得收集装置的穿透雨量Rf，进而求得收集装置的k值(4)式，判断收集装置的合理性。

(3)

(4)

2.2 参数关系分析

当任意区域为OFDE区域时，可求得模型穿透雨量Rt。

(5)

从(5)式可以看出，穿透雨量与R2、f(δ)、α呈负相关关系，与G2呈正相关关系。即冠幅半径越大、拦截能力越强，大气降雨量越小，穿透雨量越小，林木株间距G越大，穿透雨量越大。当R2趋近于无限小或G趋近于无限大时，穿透雨量无限趋近于大气降雨量Rt≈Ra。

(6)

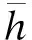
2.3 理论分析

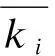
3 计 算

3.1 模型参数

建立直角坐标系(图1)。设R=3 m，H=15 m，G=7 m，根据(2)、(3)、(4)、(5)式利用Python的numpy和scipy.integrate模块计算穿透雨收集装置的k。考虑实际情况中计量仪器量程限制，设穿透雨收集装置面积为0.1～1 m2，以0.05 m2为间隔，长方形穿透雨收集装置的长宽比范围2～22，以4为间隔。为简化模型，假设f(δ)=1，a=1。

3.2 计算方法

采用两种方法进行计算分析：①网格式平分分析。将最小无重复计算单元OFDE进行网格式平分，穿透雨收集装置中心点与网格交点重合，长方形和正方形收集装置的边与OB平行，网格间距0.1 m，共1 296个交点；②OD连线平分分析。将OD平分360等份，共361个平分点，穿透雨收集装置中心点与平分点重合，长方形长边和正方形的一条边与OD平行。计算O、A、C、B为中心的树冠对OFDE内收集装置受4株树综合影响的k。满足观测条件的观测点越多，表示合理设置区域越大。计算长方形收集装置各长宽比合理设置点占比，选取最大值作为该面积的合理观测点个数。

4 结果与分析

4.1 k值分布情况

根据(6)式，利用Python的mpl_ toolkits.mplot3d模块绘制OFDE区域内k值分布情况(图2)，图中k∈[0，1.75]。k值沿树冠半径方向，逐渐增大，合理设置区域分布在树冠边缘附近，与理论分析结果相同。

4.2 网格式平分

从图3可以看出，圆形和正方形穿透雨收集装置的合理观测点数量不随穿透雨收集装置的面积而改变，长方形穿透雨收集装置合理观测点数量先随收集装置面积增加而增加，然后趋于稳定，长方形穿透雨收集装置合理观测点数量大于圆形和正方形。用Logistic模型对长方形合理观测点数做回归方程得出：

y=a/(1+b×e-cx)

式中：a=148.52，b=1.865，c=0.137。

图2 OFDE区域内k值分布情况

图3 网格式平分法各形状收集装置合理设置点占比与收集装置面积的关系

合理观测点达到148后趋于稳定，占采样点的11.4%。经计算分析得出，最优穿透雨收集装置形状为长方形，最佳收集装置面积0.35 m2，长边2.5 m，短边0.14 m。在计算过程中，长方形收集装置边长未超过林木株间距7 m，其边界只可能与以点O、A、C、B为中心的树冠产生交集，所以未超出模型计算范围，计算结果有效。

4.3 OD连线平分

从图4可以看出，圆形和正方形穿透雨收集装置的合理观测点数不随穿透雨收集装置的面积而改变，长方形穿透雨收集装置合理观测点数量先随收集装置面积增加而增加，然后趋于稳定，长方形穿透雨收集装置合理观测点数大于圆形和正方形。合理观测点数达到55后趋于稳定，占采样点的15%。最优穿透雨收集装置形状为长方形，最佳收集装置面积0.7 m2，长边3.9 m，短边0.18 m。

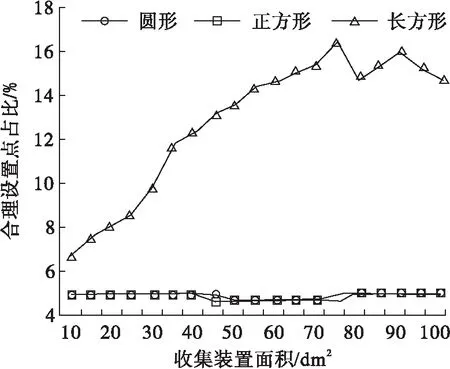
图4 OD连线平分方法各形状收集装置合理设置点占比与收集装置面积的关系

5 结论与建议

从收集装置形状方面分析，长方形是较合理的收集装置形状。在实际情况中，树种、树型、植被多样性是影响f(δ)值分布规律的重要因素，直接影响图2中k值的曲线变化，决定收集装置合理放置位置的空间区域范围。理想模型中忽略树种、树型、植被多样性等因素对f(δ)值的影响，收集装置的合理放置位置会因实际样地情况的不同，与模型的区域范围有所差异。将样地植被的f(δ)值、冠幅、空间位置等参数代入模型中，可获取更准确的收集装置合理设置参数(形状、大小、长宽比、放置方式)。模型还有待于进一步改进，与实际情况进行紧密结合，通过与实测数据对比，设计出可用于复合林穿透雨收集设置模型；通过简化参数和优化计算，为森林水文过程深入研究提供帮助。