基于优化有理函数模型的高分辨率遥感影像几何校正及其精度评估∗——以ZY-3和Pléiades卫星数据为例

张亚妮 胡德勇 于 琛 段 欣 王莎莎 刘曼晴

(1.首都师范大学资源环境与旅游学院，北京 100048；2.资源环境与地理信息系统北京市重点实验室，北京 100048)

0 引 言

近年来，随着遥感技术的迅速发展，高分辨率遥感卫星数据因其在对地观测中具有客观、宏观、快速等特点[1]，已经成为国土资源开发、地图绘制、环境检测和精准农业管理等领域的重要技术支撑之一[2]，精确地实现高分辨率遥感影像的几何校正，可以相对真实地表达影像的位置信息，是其应用的基础[3-4].因此，对高分辨率影像进行高精度几何校正具有重要价值.

伴随着遥感技术和航天技术的发展，传感器类型数量在不断增加，传感器的成像机制也越来越复杂，通常的传感器模型都是以共线方程为基础，其要求建立严格的传感器模型，但一些高分辨率商业遥感卫星如 IKONOS、Quickbird等的传感器信息暂时并不向用户公开，只向用户提供有理函数模型(rational function model，RFM)系数，在未知其轨道参数和成像有关参数的情况下，使用严格的成像几何模型处理其影像几乎是不可能的，因此引入一种独立于传感器平台不考虑其物理意义的RFM是很有意义的RFM能达到与严格成像几何模型近似的精度，并具有相对较高的计算效率[5]，具有传感器独立、物理坐标系独立、误差均衡及形式简单等特点[6]，平差结果趋于稳定，能满足传感器参数透明化、成像几何模型通用化和处理高速智能化的要求[7]，是目前高分辨率影像普遍采用的通用几何模型，所以众多高分辨率遥感卫星采用RFM作为几何定位模型[8].

针对RFM，国内外学者已经进行了大量的研究工作.Grodecki和 Dial[9]进行了IKNOS卫星影像的区域网平差研究，证明了通用的RFM比基于传感器的严密几何模型更加稳定，同时精确度也能达到相似的水平；李德仁等[10]发现仅用少量控制点，利用RFM对SPOT-5HRS进行校正，其精度就可满足于我国西部地区1∶5万地形图的测绘要求.韩杰等[11]利用资源三号(ZY-3)卫星影像附带的有理函数系数(rational polynomial coefficients，RPC)辅助文件进行定位分析，证明了RFM系统误差的存在；刘楚斌等[12]在没有地面控制点数据的情况下，利用“奋进”号航天飞机上搭载的雷达地形测绘任务(shuttle radar topography mission，SRTM)的系统数据辅助RFM进行区域网平差；唐新明等[13]基于虚拟电荷耦合器件(charge-coupled device，CCD)线阵成像技术，验证了采用像面仿射变换模型加RFM在四角点布控的方案可以获得较高平差精度.

随着地理空间信息产业的迅速发展，光学遥感卫星如雨后春笋般涌现出来，2011年法国发射了高分辨率Pléiades卫星，2012年我国在太原发射了首颗民用高分辨率ZY-3.本文基于RFM对这2种不同分辨率的遥感影像进行几何校正，利用卫星影像自带的RPC进行直接定位，通过添加地面控制点的方式消除RFM内部的系统误差，分别设置不同数量控制点的情境进行几何校正；然后，将二者校正结果的几何精度及平面位置进行验证，分析对于优化RFM不同分辨率遥感影像的适用性.

1 高分辨率遥感影像几何校正模型构建

1.1 基于RFM的几何校正

RFM系数中共有90个参数，其中有理多项式系数有80个，另外10个为归一化参数，共同构成了RFM.RFM的系统误差补偿模式可以分为物方补偿和像方补偿2种方案[14]，研究表明，基于像方补偿能够很好地消除影像的系统误差[15]，无论采取哪种参数求解都有误差，所以需要利用地面控制点来提高RFM的精度.一般有2种方式:一种方式为重新计算法，利用80个控制点直接求解RPC参数，由于参数间存在较强相关性，使求解比较困难[16]；另一种为补偿RFM系统误差法，利用外业测量的少量地面控制点，通过仿射变换解算图像的相关变换参数来补偿RFM的系统误差，在一定程度上能增强模型的稳定性[17]，本文使用第二种方法进行解算.

RFM将地面点大地坐标(由经纬度与高程表示)与其对应的像点坐标(由行列号表示)用比值多项式关联起来，为了使计算误差最小并增强参数计算的稳定性，需要对地面点大地坐标和像点坐标进行归一化处理:

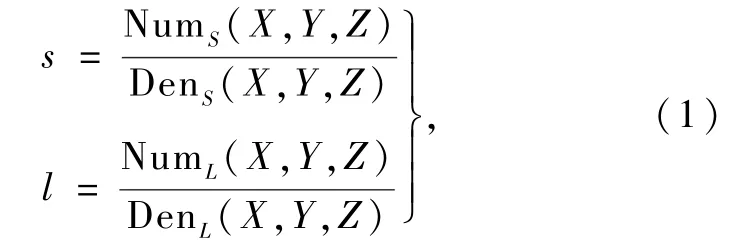
式中，(X，Y，Z)为归一化的大地坐标，(s，l)为归一化的像点坐标，其值介于(-1～+1)之间；NumS(X，Y，Z)、DenS(X，Y，Z)、NumL(X，Y，Z)和DenL(X，Y，Z)均为三次多项式，归一化系数均可从影像附带的RPC参数中获取.

相关研究表明，RFM包含一定的系统误差，采用基于像方补偿的方案能够很好地消除其对影像几何定位精度的影响[13].分析推扫式传感器卫星系统参数对影像几何定位的影响，这些误差在整个影像获取时的行向和列向上有明显的偏移，因此需要对该类误差进行修正.这里采用仿射变换法来对模型进行优化，优化数学模型如下:

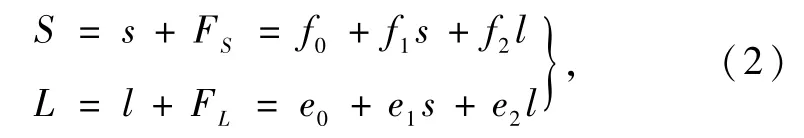
式中(s，l)为地面控制点在影像上的行列号坐标；(FS，FL)是误差在行、列方向上的改正量；(f0，f1，f2)和(e0，e1，e2)为影像的仿射变换参数，(S，L)是控制点经过平差计算后得到的像方坐标.在上式的基础上将像方补偿的仿射变换参数(f0，f1，f2)和(e0，e1，e2)作为未知数与地面控制点的归一化坐标(X，Y，Z)等未知数一并求解，即得到基于RFM的误差方程式:

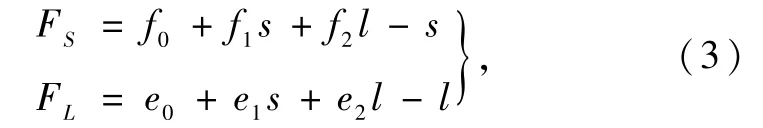
将(FS，FL)按照泰勒级数展开得到一次项:

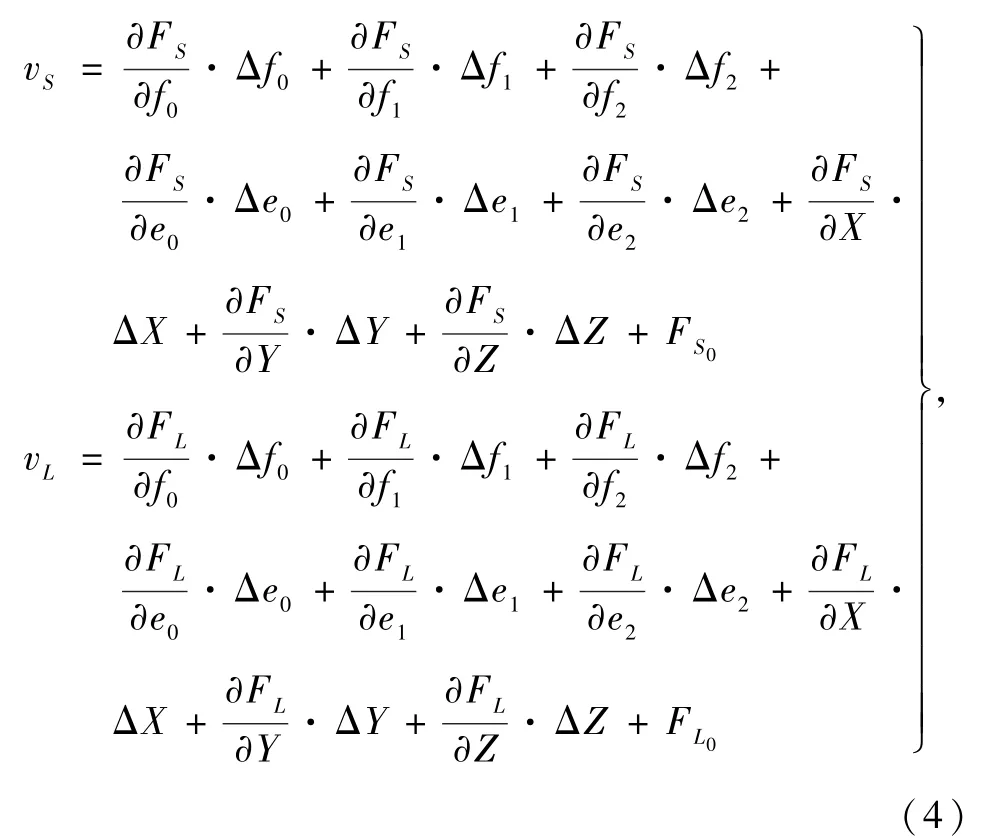
将其用矩阵的形式表示为:

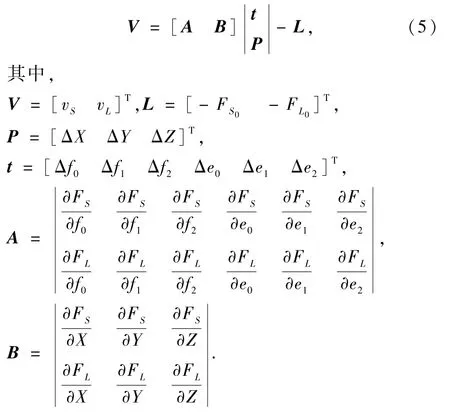
1.2 总体技术流程

本文基于RFM进行几何校正，针对每个像点可列出一组误差方程，这类误差方程中含有2类未知量:t和P，其中t对应于所有的仿射变换参数的总和，P对应于所有的待求地面点坐标.首先求解地面坐标改正数和仿射变换系数改正数.由于RFM只能提供物方到像方或像方到物方之中的某一个方向变换，反变换需要对正变换模型线性化，因此需要给定一定初始值.如果仅有1个控制点，利用求解偏移参数(e0，f0)来消除平移误差；当有2个控制点时，求解偏移参数(e0，f0)和l方向上的系数(e2，f2)来获得较高的精度[18]；当有3个及以上地面控制点时，仿射变换中的6个参数需要采用最小二乘原理通过设置阈值进行迭代计算来获得，如果改正数大于阈值，则对仿射变换参数和地面坐标进行更新，进行新一轮的迭代计算，直到整个平差过程收敛，再通过影像自带的归一化系数即可计算出较为准确地物方坐标.

本文通过构像模型分析和地面控制点优化的方式，对ZY-3和Pléiades卫星影像进行了几何校正(流程如图2所示).基于优化的RFM，通过加入不同数量的控制点反解出影像所有的偏移参数，计算得到每一个像点优化后的像方坐标，再利用RFM中的归一化参数反变换得到物方空间坐标，实现高精度的几何校正；并在不同控制点数量情境下，基于检查点对2种卫星的高分辨率遥感影像几何校正的结果进行精度验证及对比分析.同时，将其与通过四角布设控制点进行几何校正的影像进行对比[14].

图1 总体技术流程

2 研究区与数据

2.1 研究区

本文选取了 ZY-3和 Pléiades卫星的高分辨率遥感影像进行几何校正，具体影像信息见表1.选择的实验区为北京市主城区奥体中心及周边区域(图2)，范围为(116.361°～ 116.420°E，39.967°～40.014°N)，覆盖面积大约5 km ×5 km，涵盖了国家体育场“鸟巢”、国家体育馆以及居民区等区域，其覆盖类型主要包括建筑、道路、植被、水域以及裸地等，该研究区内地形较平坦，地面海拔约为30 m.

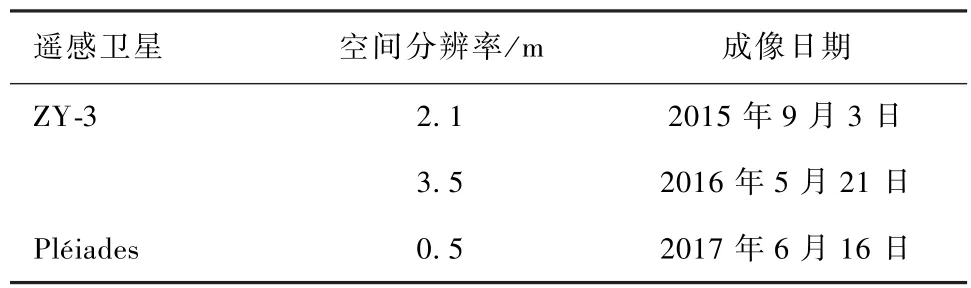
表1 高分辨率遥感影像信息

2.2 采样点测量及实验设计

进行外业测量时以ZY-3卫星影像为参考数据，在充分考虑实际操作的安全性、可通达性等情况下，选取在影像上易于分辨的明显地物特征点为采样点，如道路交叉口和体育场草坪拐角等(图2).为减少偶然误差使其尽量均匀地分布在整个研究区内，既有在建筑密度高、形态复杂的区域，也有在低层居民楼、奥林匹克公园等地形平坦的区域，以保证控制点及检查点的代表性和准确性.由于分辨率不同等因素针对ZY-3和Pléiades卫星的影像选取不同的控制点，具体分布如图3所示.

在实验区内采用基于载波相位观测值的实时动态(real-time kinematic，RTK)定位技术，这是一种基于载波相位观测值的定位技术，能够实时地提供测站点在指定坐标系中的三维定位结果.工作模式采用连续运行基准站(continuously operating reference stations，CORS)模式，通过接收卫星信号获得所在地点的位置数据，利用设备的差分解算功能，结合原始观测值和差分数据进行解算实现纠偏，以此获得高精度的点位坐标.共获取了50个均匀分布的高精度采样点的三维坐标，作为几何校正中的控制点条件及后期验证数据，每个点平均采测10次，后期剔除误差大的点，并进行均值化处理，外业采样点量测精度能够达到厘米级.

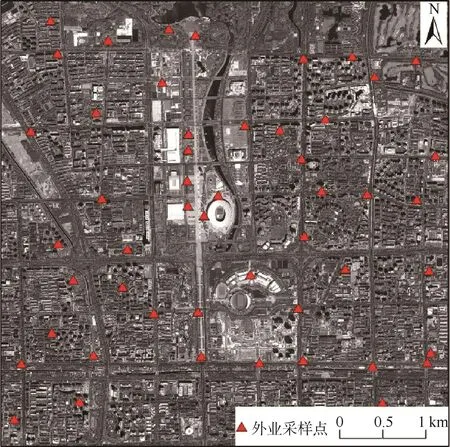
图2 研究区范围及采样点位置

图3 控制点分布

为比较不同数量的控制点对高分辨率遥感卫星影像的几何校正精度，在实验区同一套外业GPS采样点数据的支持下，采用以下几种方案进行对比实验，见表2.

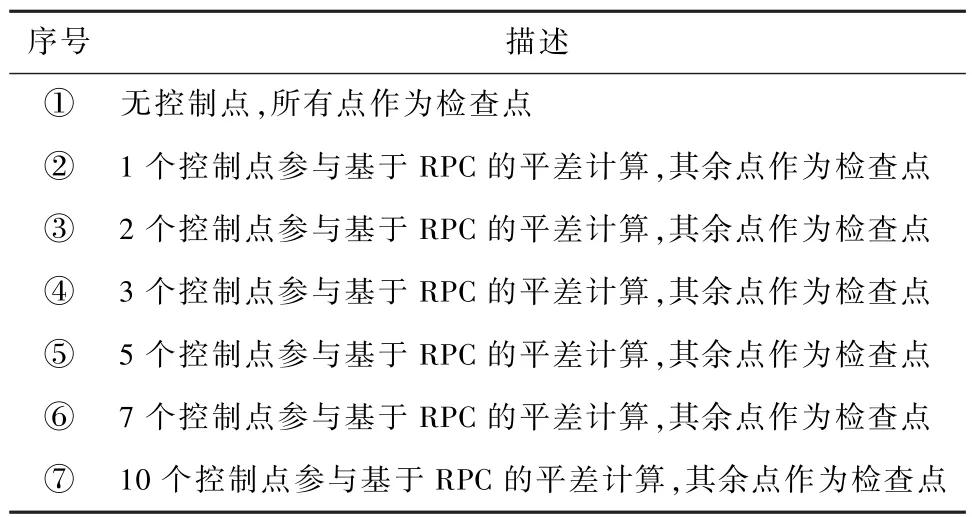
表2 实验分组情况

3 实验结果与精度分析

3.1 ZY-3卫星影像几何校正误差分析

为了对比添加不同数量控制点后校正结果的差异，本文分别计算了不同情境下检查点在X、Y及平面方向偏移距离的平均值及中误差(即均方根误差).从实验结果表3可以看出，在无控制点的情况下，ZY-3卫星影像经过附带的RPC参数进行校正后，2015年9月3日和2016年5月21日拍摄的影像几何定位平面误差均值分别高达40.14和10.38m；依次增加1、2、3、5、7和10个控制点进行校正后，影像的误差均值及中误差均有大幅度的降低，可降至5.00 m以下.实验结果表明，在实验区域中增加1个控制点时，其平面精度明显改善，随着控制点数量的增加，其精度缓缓提高.根据趋势来看，通过加入控制点进行平面精度优化的方法得到的校正结果已趋于稳定.

因不同数量的控制点设置方案会对影像平面位置有所影响，进而选取不加控制点与加入10个控制点后几何校正的影像进行对比分析.当不添加控制点仅采用影像自带的RPC参数进行校正时，2015年9月3日拍摄的影像上的检查点整体相对于实际采样点往西南方向偏移，如图4(a)所示，平面误差较大；加入10个控制点后对纬度方向的偏移改正十分明显，影像整体相对于采样点往西方向偏移，平面误差明显减小.2016年5月21日拍摄的影像在加入控制点校正后整体均往西方向偏移，如图4(b)所示，对于偏移距离的纠正也十分明显.

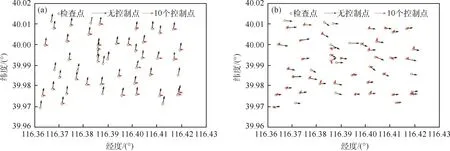
图4 ZY-3卫星影像几何校正检查点平面误差分布对比

实验结果表明，当ZY-3卫星影像的几何畸变较大时，可以通过添加控制点的方式优化RFM进行几何校正，其影像平面位置精度可以得到大幅改善，且加入10个控制点时影像校正结果最优并趋于稳定，平面位置整体向西偏移保持在1～3个像元.

3.2 Pléiades卫星影像几何校正误差分析

从实验结果表4可以看出，在无控制点的情况下，Pléiades卫星2017年6月16日拍摄的影像经过其自带的RPC参数进行校正后，几何定位平面误差均值为7.20 m，中误差为7.22 m；依次增加控制点后误差精度得到一定改善，平面误差的均值及中误差可分别降低至2.95和3.02 m.由此得知，在实验区域中增加1个控制点时，其平面精度能得到明显改善；随着控制点数量的增加，精度提升不再明显.

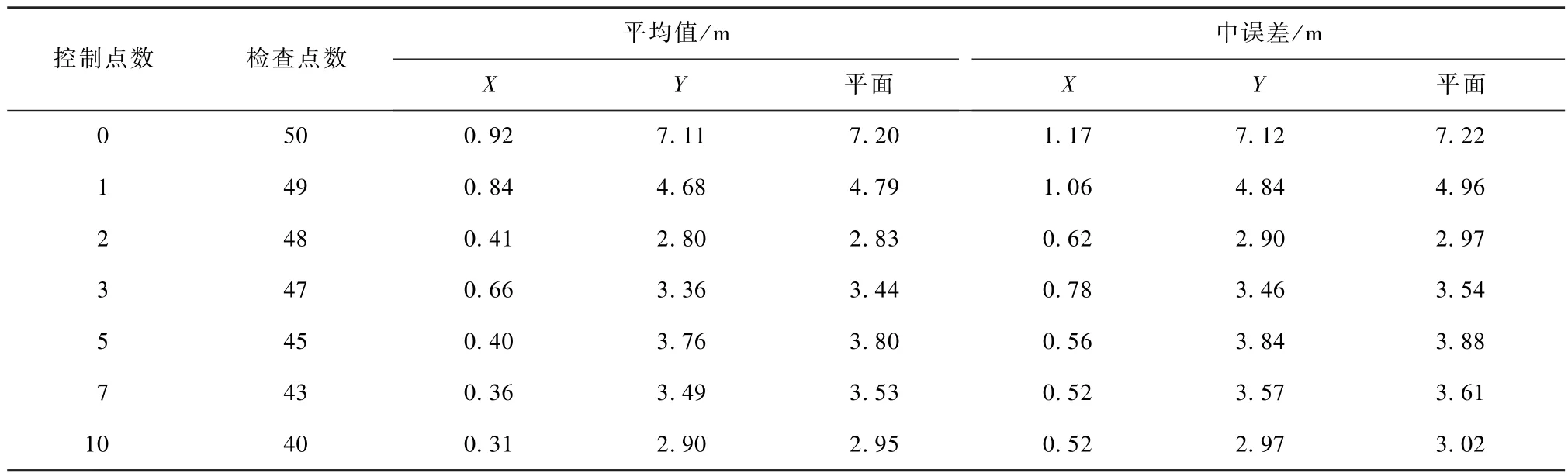
表4 Pléiades卫星2017年6月16日影像几何校正平面定位精度

对 Pléiades卫星 2017年 6月 16日拍摄的影像，选取不加控制点及加入10个控制点后的几何校正结果进行对比分析发现，影像上的检查点在增加不同数量控制点后整体相对于实际采样点均往北方向偏移(图5).

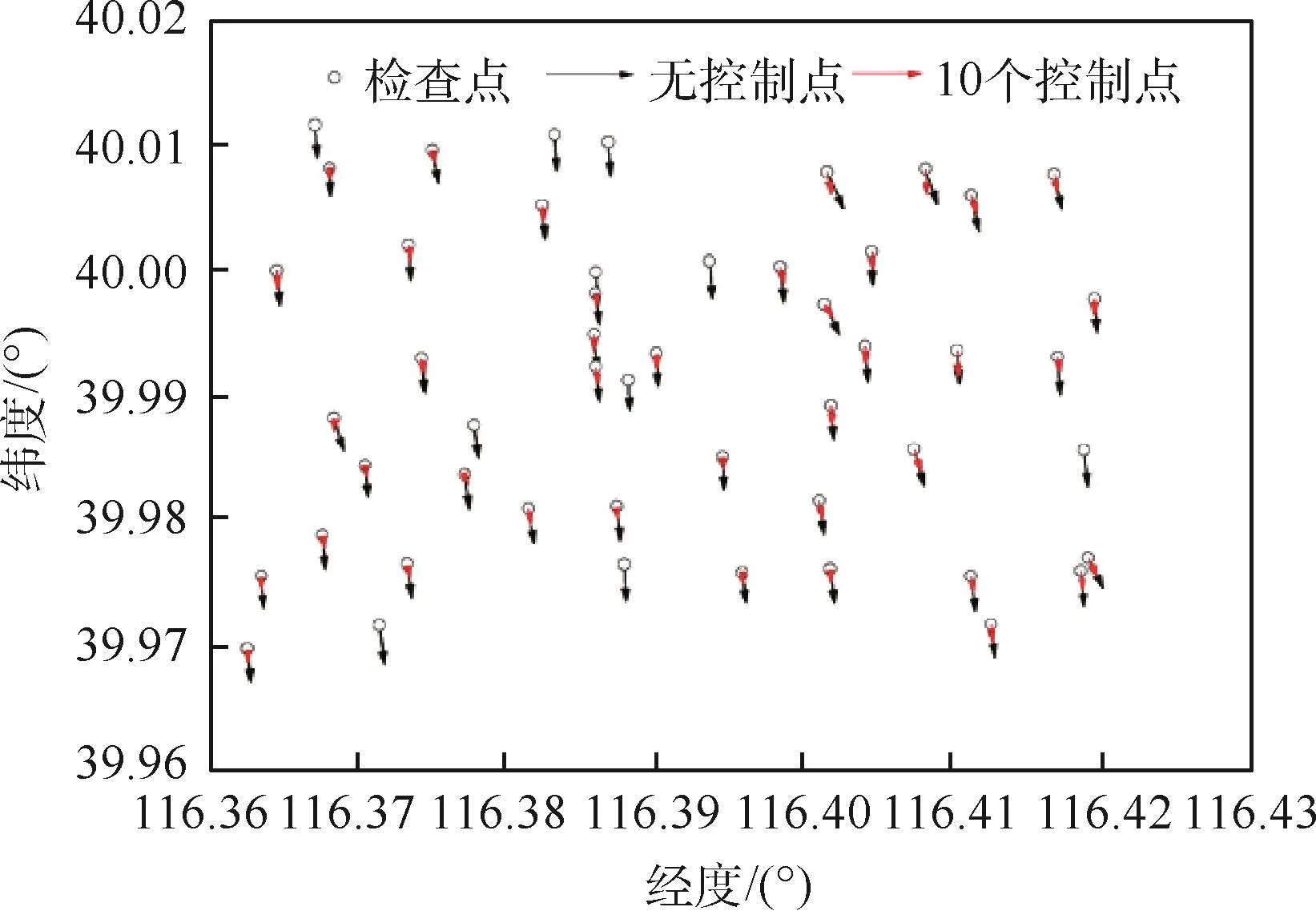
图5 Pléiades卫星几何校正检查点平面误差分布对比

3.3 几何精度验证与对比

通过对ZY-3和 Pléiades卫星高分辨率遥感影像几何校正结果进行对比，由图6可知，基于优化的RFM的几何校正均可不同程度地提升其平面精度，尤其是当影像偏移比较明显时，基于单个控制点对系统误差的校正效果十分明显.增加控制点后略微提升平面精度，说明2种高分辨率遥感卫星的影像内部本身的几何畸变较小，已达到了较高的精度水平.

同时，将2种卫星的高分辨率遥感影像采用四角布设控制点的方式进行几何校正，通过检查点进行精度验证，结果显示，2015年9月3日及2016年5月21日拍摄的2景ZY-3卫星影像的平面误差均值分别为7.89和4.22 m，2017年6月16日拍摄的Pléiades卫星影像平面误差均值为 3.62 m.从图 6可以看出2种卫星影像基于优化RFM后的平面误差可降至5.00 m以下，较优于四角布设控制点的校正结果.

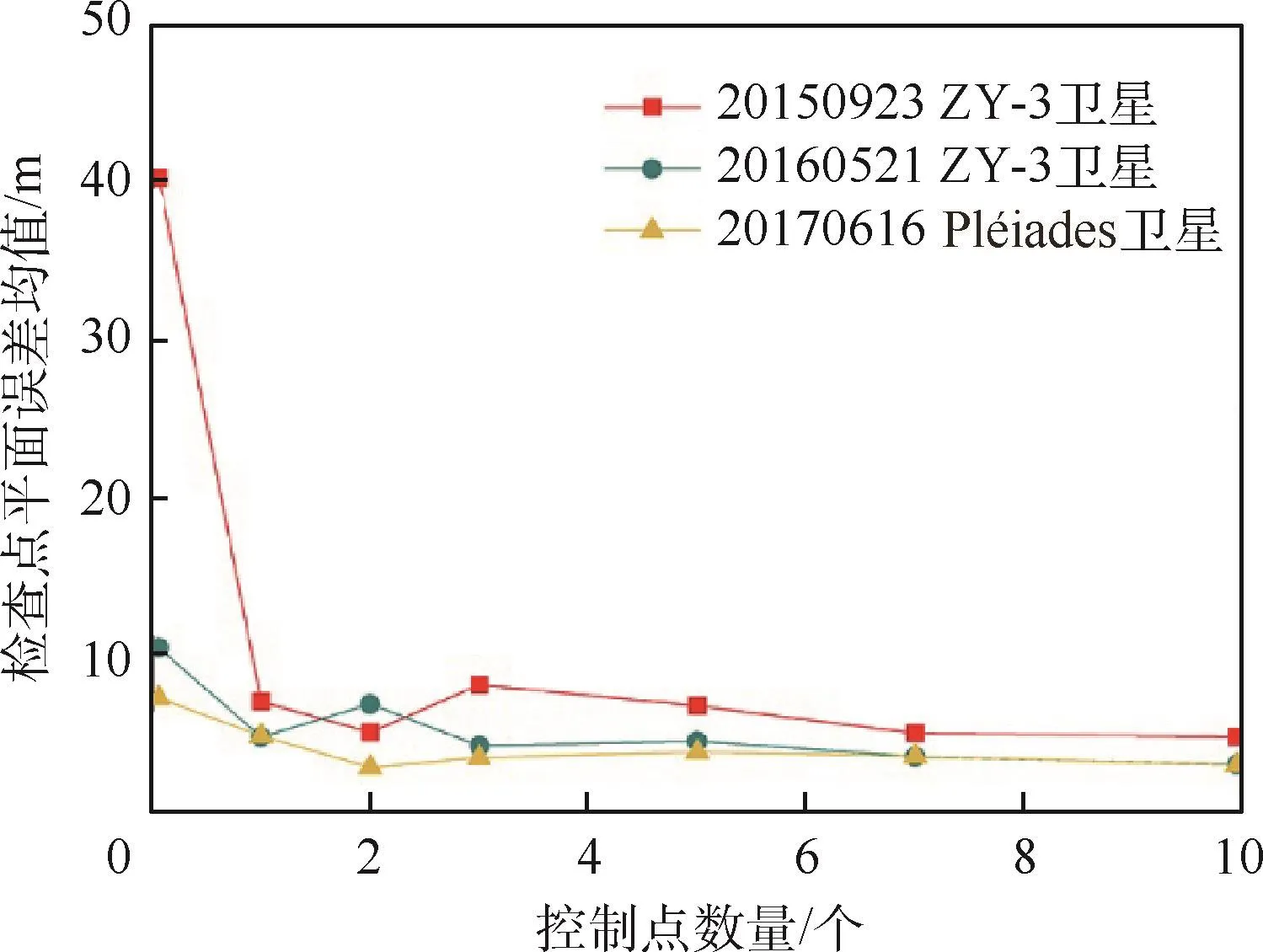
图6 高分辨率遥感影像几何校正精度对比

4 结 论

本文在RFM的基础上推导分析了优化参数的解算方式，并设计了不同数量控制点的实验方案，从检查点的定位精度及平面位置2方面分析了ZY-3和Pléiades卫星影像几何校正的效果.结果表明:

(1)本文验证了通过添加控制点的方式，基于优化RFM的几何校正可以不同程度地提升ZY-3和Pléiades卫星高分辨率影像的平面几何精度，提升效果明显，且在卫星运行稳定的前提下影像平面误差均可降至5.00 m以下.通过验证与对比显示了该种方法应用于不同传感器高分辨率遥感影像几何校正的适用性，其结果较四角布设控制点进行几何校正的结果更加稳定.

(2)不同数量控制点的设置方案会影响高分辨率遥感影像的几何定位精度及平面位置.未加入控制点时，影像通过自身所带的有理多项式系数进行校正，其检查点相对于实际采样点的位置均有不同方向及距离的偏移，2015年 9月 3日和 2016年5月21日拍摄的2景ZY-3卫星影像平面误差分别高达40.14和10.38 m，2017年6月16日拍摄的Pléiades卫星影像平面误差为7.20 m；当添加1个控制点对RFM进行优化后，发现影像定位精度明显提高，2景 ZY-3卫星影像平面误差分别降低至6.96和4.72 m，Pléiades卫星影像平面误差降低至4.79 m.然而随着控制点数目的增加，平面误差略微降低但整体偏移方位改变不大.

本文探讨了通过添加不同数量控制点优化RFM的方法对高分辨率遥感影像几何定位精度的影响，由于受实验条件等限制，研究有待从以下几个方面进行改进:1)分析选取不同位置的控制点是否会对影像校正精度产生进一步的提升；2)当研究区范围较大时是否需要增加控制点才能达到较为准确的几何校正效果；3)验证该方法应用于山地、丘陵等区域时，不同传感器的高分辨率遥感影像的校正精度如何.