基于微分法串联机器人的误差敏感度分析

陈 华,刘新宇,赵学峰

(1.马鞍山学院 人工智能学院,安徽 马鞍山 243100;2.江南大学 机械工程学院，江苏 无锡 214000;3.中达电子(江苏)有限公司,江苏 苏州 215000)

串联机器人的性能衡量主要取决于重复性和精确性这两个重要的评价标准.其中可重复性被定义为机器人能够精确地移动到先前指定点的能力.精确度是由末端执行器能够移动到指令点的精度来表示的.但目前,大多数工业机器人通过应用在线编程方法执行任务,工作精度和效率相对较低.

随着离线编程技术引入到机器人行业,离线编程技术的优势已经逐步得到人们的认可.由于在离线编程模式下工作,提高了机器人工作效率,比教学模式更适合复杂的操作.而且一般离线编程技术应用现有CAD 数据及机器人理论结构参数所构建的机器人模型与实际模型之间存在误差,因此位置精度变得至关重要[1].文献[2]研究表明:工业机器人的重复性比位置精度好得多,且位置精度受机器人重复性的限制.在保证良好的可重复性前提下,可以应用标定技术来提高机器人的精度.由于一些影响因素(如振动、制造和装配误差)的存在使得机器人运动学参数存在误差.目前大多研究只关注末端位姿误差的分析,先分析单个类型运动学变量对末端的影响,再把所有类型运动学变量对末端位姿的影响进行线性叠加.但在研究影响串联机器人手腕位姿的误差中,发现其主要误差还包括非标机械零部件的加工精度误差、各部分装配间隙误差和标准件的精度误差,以及温度变化、动负载等作用使得机器人杆件产生的柔性变形.此外,传动误差和控制系统误差(控制算法本身的缺陷)也使得误差分析模型显得非常复杂和缺少规律可循[3].显然这类分析方法忽视了运动学几何参数的综合作用对末端执行器位姿的影响.这些机器人运动学参数的误差很小,但也会给机器人末端执行器造成很大的偏差，因此机器人误差敏感度分析显得格外重要.

为了提高串联机器人的绝对定位精度,笔者提出一种基于微分法和矩阵法对串联机器人进行误差源分析的方法.先分析单个连杆姿态矩阵的微小误差,再采用积分法分析N个连杆末端的位姿误差,采用微分法和修正Denavit-Hartenberg(MDH)运动学模型(增加了第5个参数的Denavit-Hartenber(DH)方法),将其先绕x轴旋转,再绕z轴旋转,对末端位姿误差的敏感度进行分析.

1 机械手的函数误差模型的构建

为简化几何误差的模型,目前研究都是将其误差主要来源归结于结构参数误差和运动变量误差[4-5].假设机械手的位姿误差与各连杆的结构参数误差和运动变量误差存在线性关系,即可采用传递矩阵法构建机械手的函数误差模型.

由MDH法可知相邻坐标系齐次变换矩阵为

transzi-1(di)rotzi-1(θi)transxi(ai)rotxi(αi)rotyi(βi)，

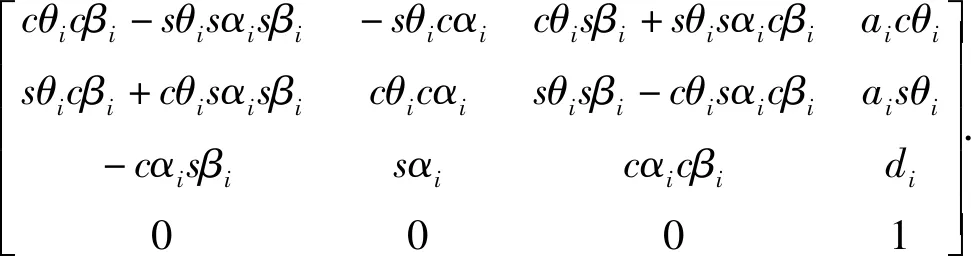
(1)

式中：cθi=cosθi;cβi=cosβi;sθi=sinθi;sαi=sinαi;sβi=sinβi;cαi=cosαi.

由式(1)可知:关节坐标系从i-1变换到i,完全由连杆的4个参数,即关节转角θi、关节扭角αi、连杆偏距di和连杆长度ai所决定.依据MDH模型,创建选择顺应性装配机器手臂(SCARA)连杆的坐标系示意图[6].图1为各连杆的坐标系示意图.

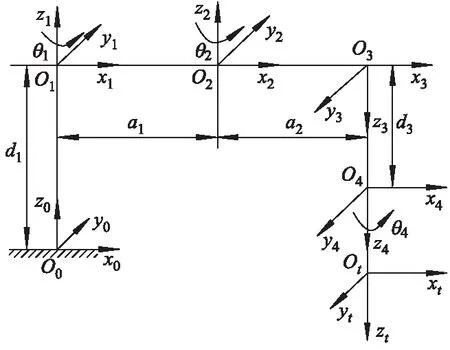
图1 连杆坐标系示意图

假设SCARA机械手末端法兰坐标系原点与标定杆件坐标系的原点重合,且末端法兰坐标系和标定杆件坐标系的各坐标轴平行,可得到2个坐标系之间的齐次变换矩阵:

(2)

式中:tx,ty和tz为标定杆坐标系相对于末端法兰坐标系的变化值.

机械手末端标定杆的测量点位姿相对于基坐标系中的位姿模型为

(3)

2 单个连杆误差分析

由方程(1)可知,4个关节变量分别为θi,αi,di和ai.关节分为旋转关节和平移关节.对于旋转关节,θi为关节变量,其他参数值为已知变量.对于平移关节,di为关节变量,其他参数值为已知变量.如果连杆参数存在微小误差,就会产生关节变量误差dAi.因此两个坐标系的精确位置变化为Ai+dAi,其中dAi与连杆参数的线性关系表示为

(4)

式中:Δθi为旋转关节转角误差;Δdi为平移关节位移误差.

3 N自由度串联机器人的误差分析

以SCARA串联机器人为研究对象,其末端执行器的位姿误差主要来源于3个部分:① 机器人连杆参数误差造成末端法兰位姿误差,其连杆参数误差主要包括θi,αi,di和ai的误差;② 由于平行关节的齐次变换,引入关节角度βi的微小变化,导致机器人末端执行器位姿误差;③ 机器人末端法兰所连接的工具由于存在加工误差,所以也需要误差分析[7].

首先建立N个自由度串联机器人末端位姿误差分析数学模型.根据前面单个连杆的误差分析,可以得到N个自由度串联机器人末端位姿误差相对于基坐标系的位姿误差模型.设末端法兰坐标系对于基坐标系的变换矩阵为TN,其误差矩阵为dTN,得到线性方程:

TN+dTN=(A1+dA1)(A2+dA2)…(AN+dAN)=

(5)

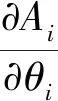
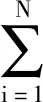
(6)

为了将式(6)描述得更为简单,将机器人末端坐标系到第i个机器人关节坐标系的变换矩阵定义如下:

ui=AiAi+1…AN.

(7)

dTN=TNδTN,

(8)

(9)

因此N个自由度关节末端执行器的误差矩阵可以描述为

(10)

第i个机器人关节坐标系的连杆误差矩阵可以描述如下：

(11)

定义如下表达式:

(12)

(13)

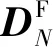
(14)

式(14)表明:各关节DH参数误差引起的末端位姿误差的线性叠加是造成机器人末端位姿误差的根源.因此有

(15)

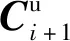
(16)

把式(15)和式(16)代入式(14)中,可得到下列表达式:

为有序推进工程建设施工进度，在保障工程质量的前提下，要努力做到：一是及时检查施工方案的执行情况，督促施工队落实方案的进度，检查原材料和半成品的进场情况并及时纠正不切实际的施工方法。二是做好原材料的采购和进场准备，为施工队制定施工计划提供保障。三是做好施工协调工作，如对影响施工的停水停电，要积极主动排除故障，避免停工损失等。

(17)

(18)

(19)

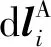
由于机械手末端相对于其基坐标系微分运动可以分解为机械手末端相对于其基坐标系的微分平移和微分旋转,所以式(17)-(19)又可写成

(20)

(21)

(22)

(23)

(24)

(25)

依据坐标系的微分运动及矩阵理论等知识,可以推导出关于N自由度串联机器人末端执行器相对于基坐标系的位姿误差公式,将上述的理论成果应用于串联机器人的位姿误差分析.

为此,HAYATI等专家学者提出了MDH模型,同时还提出围绕y轴旋转的参数影响,由于考虑参数影响的复杂性,通过具体问题具体分析,就可得到机器人末端执行器的位置误差模型和姿态误差模型[8].

位置误差模型见公式(26)-(28).姿态误差模型见公式(29)-(31).

dx=-Δθ1{cα1[a2cθ2s(θ4-θ2)+

a2sθ2c(θ2-θ4)]+a1cα1s(θ4-θ2)+

d3sα1c(θ2-θ4)}-Δθ2(a2cα2sθ4+

d3sα2cθ4)+cθ4Δa2+cθ4Δa3+Δa4-

d3s(θ4-θ2)Δα1-d3sθ4Δα2-d3sθ4Δα3-

sα1s(θ4-θ2)Δd1-sα2sθ4Δd2+sα3sθ4Δd3，

(26)

dy=Δθ4a4cα4+Δθ3(a3cα3cθ4-d3sα3sθ4)-

Δθ2(a2cα2cθ4-d3sα2sθ4)-Δθ1{cα1[a2cθ2×

c(θ2-θ4)-a2sθ2s(θ4-θ2)]+a1cα1c(θ2-θ4)-

d3sα1s(θ4-θ2)}-s(θ4-θ2)Δa1-sθ4Δa2-

sθ4Δa3-d3c(θ2-θ4)Δα1-d3cθ4Δα2-

d3cθ4Δα3-sα1c(θ2-θ4)Δd1-

sα2cθ4Δd2+cθ4sα3Δd3+sα4Δd4，

(27)

dz=Δθ1(a1sα1+a2sα1cθ2)+Δθ2a2sα2-Δθ4a4sα4-

a2sθ2Δα1-cα1Δd1-cα2Δd2+cα3Δd3+cα4Δd4.

(28)

δx=Δθ1sα1s(θ2-θ4)-Δθ2sα2sθ4+c(θ2-θ4)Δα1+

cθ4Δα2+cθ4Δα3+Δα4，

(29)

δy=-Δθ1sα1c(θ2-θ4)-Δθ2sα2cθ4+Δθ4sα4+s(θ2-

θ4)Δα1-sθ4Δα2+cθ4Δα3,

(30)

δz=-Δθ1cα1-Δθ2cα2+Δθ4cα4.

(31)

式中：s(θi-θj)=sin(θi-θj);c(θi-θj)=cos(θi-θj).

4 MDH模型的运动学参数误差分析

DH运动学模型为使用一个4×4的齐次变换矩阵描述相邻关节坐标系的空间关系,推导出末端执行器相对于参考系的等价齐次变换矩阵.根据DH模型，机器人末端位姿方程函数包含ai,di,αi和θi等4个参数,它们都存在实际偏差.假设存在误差Δai,Δdi,Δαi和Δθi,参数可以修正为

(32)

将上式带入DH模型的运动学方程,便可求出其对应的MDH模型.由单一变量控制法可知,设置某个关节的一个参数误差,其他未知参变量值为0,依次改变关节变量值,即可得到相应关节的误差分布曲线.

4.1 关节转角零位偏差的敏感性分析

影响末端位姿精度的重要因素之一是关节转角零位偏差.以q=[π/3 π/4 3π/4 π/2]为基本位姿,分析关节转角零位误差对于末端位姿敏感性的影响.

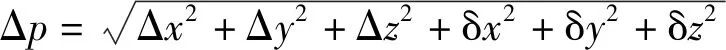
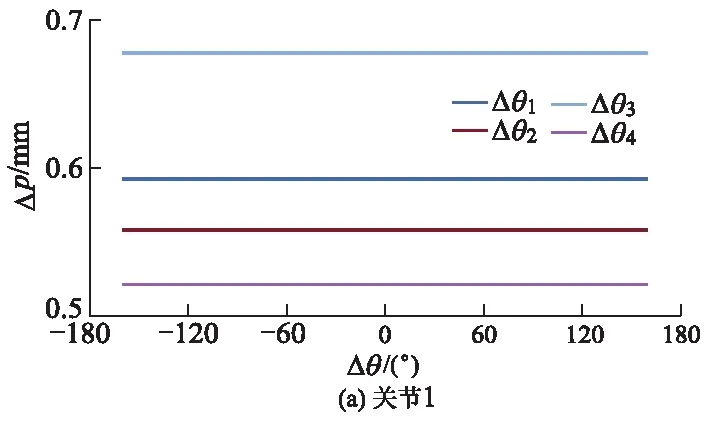
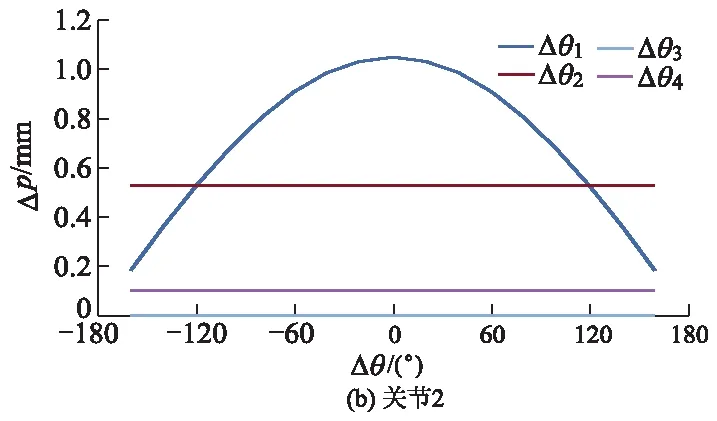
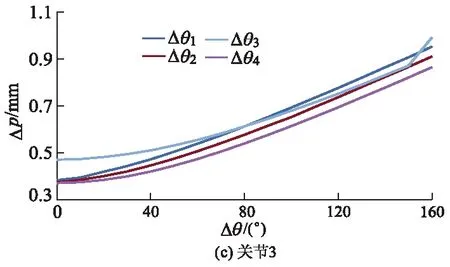
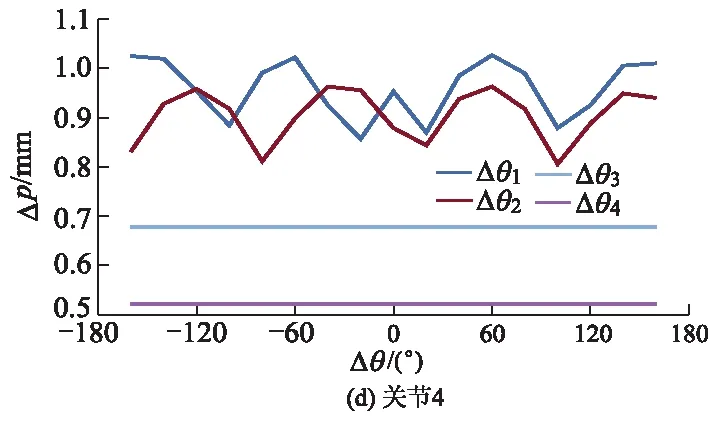
图2 关节转角误差与末端位姿误差的关系曲线

由图2可知:关节转角变化所产生的误差对末端位姿的影响程度由大到小分别为Δθ4，Δθ2，Δθ3和Δθ1;Δθ4对末端位姿精度的影响最为显著,Δθ1对末端位姿精度的影响较小.因此,在机器人的工业生产中,需要合理规划机器人的路径,应当避开对末端位姿精度影响程度较大的奇异点.当所有转动关节的转角零位均存在0.01°误差,以及第3移动关节存在0.01 mm的末端位姿误差时,取各关节转角零位误差对末端位姿影响误差的平均值,可以得出关节1,2,3和4转角零位误差对应的平均值分别为0.721 9,0.645 6,0.500 2和0.427 1 mm.

可见，关节转角零位误差对于机器人末端位姿的影响程度由大至小分别为Δθ1,Δθ2,Δθ3和Δθ4.在机器人末端位姿的连杆传递过程中,一个较小的关节转角误差将导致末端位姿产生一个较大的误差[9].由此还可以看出产生转角误差的关节离机器人基座的距离越靠近,对机器人末端位姿的影响也会越大,而且4个关节转角零位误差对机器人末端位姿的影响各不相同,其中对末端位姿影响最大的第1个关节转角误差约为第4个关节的1.69倍.

4.2 关节扭角零位偏差的敏感性分析

首先取q=[π/3 π/4 3π/4 π/2]为初始基本位姿,同时假设存在关节扭角误差Δαi=0.01°,其他的结构参数没有误差,从而分析关节扭角零位误差对末端位姿敏感性的影响情况,得到关节扭角误差对机器人末端位姿影响的分布曲线，如图3所示.

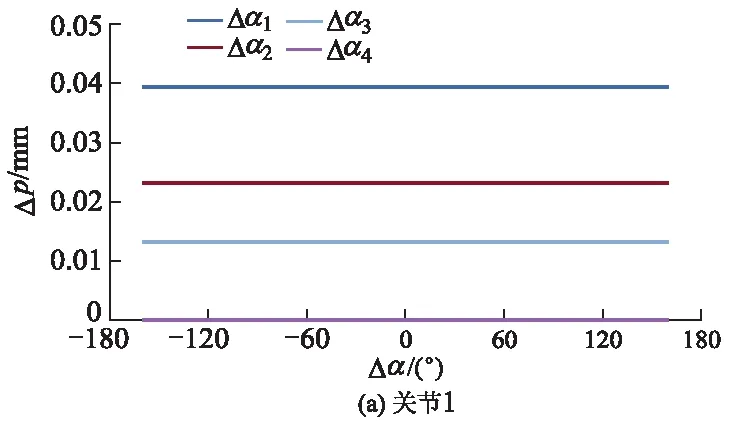
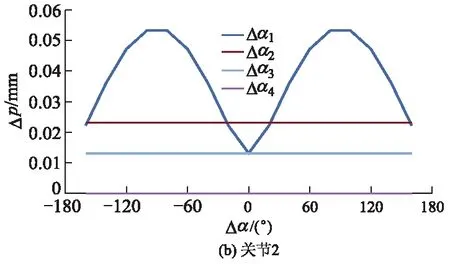
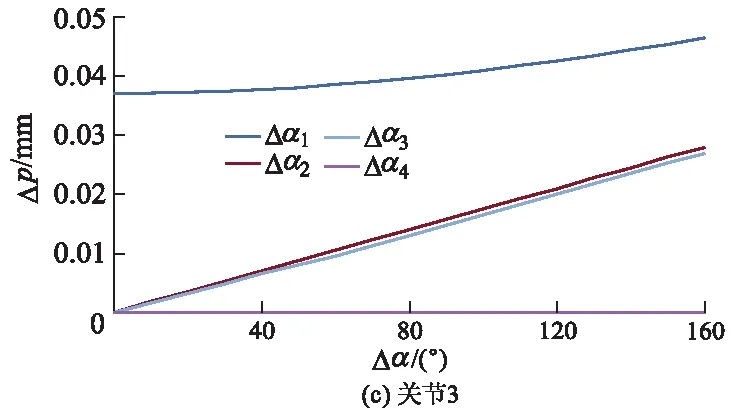
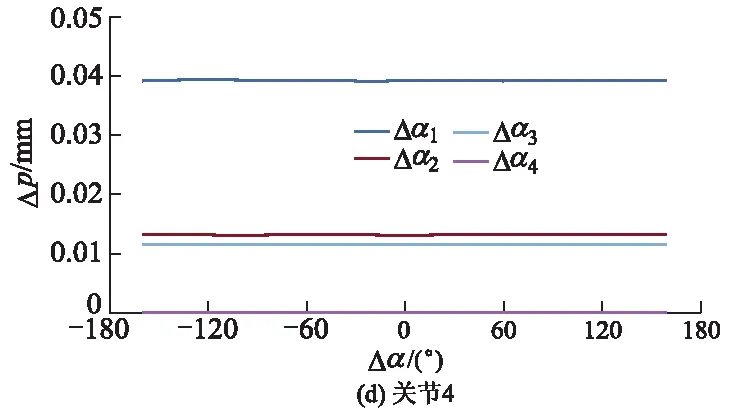
图3 关节扭角误差与末端位姿误差的关系曲线

当机器人所有转动关节的扭角零位存在0.01°误差,以及第3移动关节存在0.01 mm末端位姿误差时,取各关节扭角零位误差对末端位姿误差的平均值,可以得出关节1,2,3和4的扭角零位误差对应的平均值分别为0.039 3,0.018 3,0.012 7和0 mm.

可见,关节扭角零位误差对于机器人末端位姿的影响程度由大至小分别为Δα1,Δα2,Δα3和Δα4.在机器人末端位姿的连杆传递中,一个较小的关节扭角误差也会导致末端位姿产生一个较大的误差,同时发现产生扭角误差的关节位置离机器人基座的距离越近,对末端位姿的影响越大.且4个关节扭角零位误差对末端位姿的影响也各不相同,其中对末端位姿影响最大的Δα1约为Δα3的3.09倍.

4.3 连杆的长度误差和偏移误差敏感性分析

由于机器人的零件加工制造、装配和轴承轴向定位等影响,会产生连杆的长度误差和偏移误差[10].假设分别存在连杆长度误差和偏移误差均为0.1 mm,其仿真方法与前述相同,得到连杆的长度误差和偏移误差对机器人末端位姿影响的分布曲线，如图4所示，其中φ为关节空间运动角度.

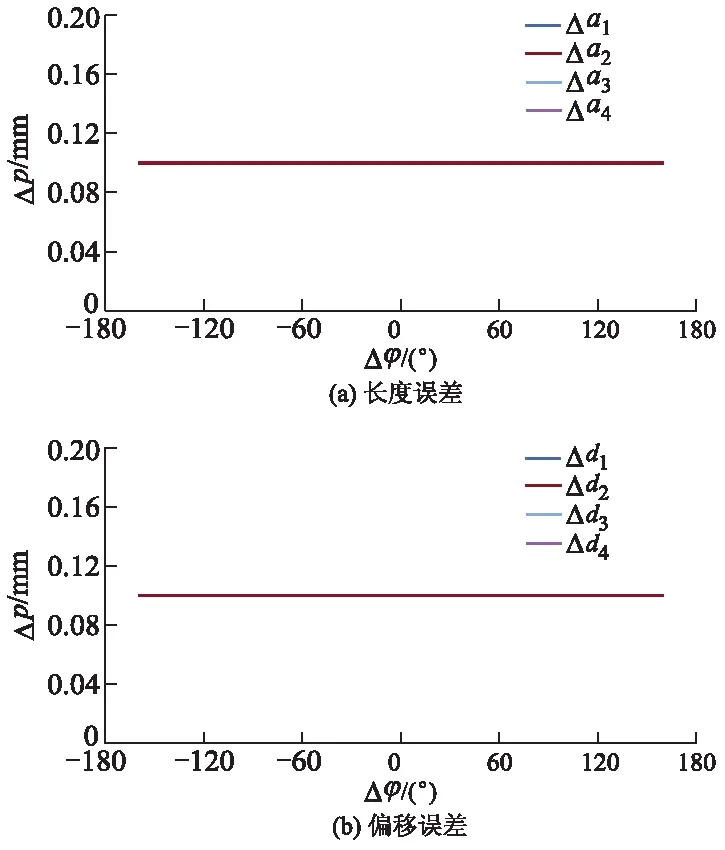
图4 长度误差和偏移误差对末端位姿影响分布曲线

由图4可知:连杆长度误差和偏移误差对末端位姿都产生了0.1 mm的误差,但是该误差值在串联机器人移动中基本上不影响机器人位姿,其等效传递不存在放大和缩小误差,且机器人的4个关节角度的变化均不改变末端位姿误差值.

5 结 论

1) 根据误差的仿真分析结果可知:关节角度误差分析中,关节转角误差产生的影响较关节扭角误差产生的影响更大;在连杆的误差敏感性分析中,连杆长度误差较连杆的偏移误差产生的影响更大.

2) 由串联机器人末端位姿误差分析可知:关节角度误差比连杆长度误差产生的影响更大;角度类参数产生误差的关节位置与串联机器人基座间距离越近,对末端位姿的影响也越大,具有明显的放大误差功效;长度类参数对串联机器人末端位姿的影响仅有等效作用,不具任何放大和缩小误差作用.