西藏高原灌区参考作物蒸散量模型的适用性研究

蒙 强，刘静霞，李玉庆，张文贤

(西藏农牧学院水利土木工程学院，西藏 林芝 860000)

参考作物蒸散量(ET0)是作物系数法计算作物需水量、制定农业灌溉制度及评价区域水资源的重要参数。近年来，随着蒸散理论研究的深入，一系列基于温度、辐射、风速及综合气象参数的ET0计算模型被广泛应用于蒸散量的估算中。其中，FAO 56 Penman-Monteith(FAO 56 PM)模型综合考虑了所有气象因子对ET0的影响且具有较完整的理论，被国际公认为是ET0计算的标准方法，且常被用于修正及评价其他ET0模型的精度和适用性[1]。此外，国内学者关于ET0计算方法及其适用性的研究结果已充分证明了FAO 56 PM法在我国具有较高的计算精度[2-4]，但其计算过程较为复杂且需要完整的气象资料，故无法应用于气象资料缺失条件下的ET0计算。对此，学者发展了多种ET0的简化模型，例如FAO 24Radiation、Hargreaves-Samani、Makkink等，但上述模型大多是针对特定的区域及气候条件而提出的，已有的研究结果表明其计算精度及适用性存在一定的地域差异。例如，樊军等[5]通过对比多种ET0模型在陕西省的适用性，指出Priestley-Taylor模型的模拟值最接近于FAO 56 PM模型的计算结果，FAO-24 Blaney-Criddle、FAO-24 Radiation、Hargreaves-Samani及Makkink 4种模型与FAO 56 PM模型的模拟值间存在明显的差异。李志[6]研究认为FAO-24 Blaney-Criddle、Hargreaves-Samani模型在黄土高原区有较好的适用性，但FAO-24 Radiation、Priestley-Taylor、Makkink模型对ET0的模拟效果较差。余婷等[7]的研究结果表明，在我国西北地区Kimberly Penman、FAO 1979 Penman、FAO 24 Penman、FAO 1948 Penman、FAO 79 Penman、Hargreaves-Samani、Mc Cloud、Hargreaves-Samani、Priestley-Taylor-1、Priestley-Taylor-2、FAO-24 Radiation、Makkink、Irmark-Allen、Irmark 这14种模型的模拟精度存在明显差异，其中FAO 1948 Penman、Hargreaves-Samani、Priestley-Taylor-1的模拟精度最高。徐冰[8]等关于西藏高寒牧区ET0模型适用性的研究结果表明，FAO 1979 Penman、Irmark-Allen模型模拟值较FAO 56 PM总体偏大，Priestley-Taylor模型的模拟值误差最小，并指出Hargreaves-Samani模型可作为高海拔区域的ET0在气象资料短缺条件下的简化算法。

然而，西藏高原特殊的地形地貌及气候环境给作物需水量的准确估算带来了一定的困难，为降低作物需水量估算的不确定性，提高农业灌溉用水效率，开展ET0计算模型的适用性评价具有重要的现实意义。但西藏地区有关ET0的理论研究起步较晚，已有的研究大多是关于ET0的时空分布及变化特性的分析，而关于ET0计算方法的分析对比及适用性探讨的研究则明显不足。因此，本研究选取西藏高原3座典型灌区为研究区域，基于长系列的灌区气象数据，利用目前常用的FAO 17 Penman、Hargreaves-Samani、Makkink、Priestley-Taylor、Irmark-Allen 5种模型计算ET0值，并以FAO 56 Penman-Monteith公式的计算值为标准，对5种ET0计算模型的适用性进行评价，旨在为西藏高原灌区开展高效节水灌溉及优化配置农业水资源提供技术参考。

1 数据与方法

1.1 研究区概况及数据来源

西藏的灌区主要分布在日喀则(2 416 座)、山南地区(1 957 座)。其中，满拉、墨达、江北灌区分别位于日喀则、拉萨、山南地区，是西藏高原上的大型灌区，灌溉面积均超过2 万hm2。根据《西藏农业气候资源区划》结果，满拉、墨达、江北灌区位于半干旱农业区。本研究在综合考虑了灌区面积、行政区划、农业种植等情况下，选取满拉、墨达、江北3个灌区为本文的典型研究区域，各灌区基本资料见表1。满拉、墨达、江北灌区附近的气象站点分别为江孜、墨竹工卡和贡嘎，各站点的逐日气象资料来源于中国气象数据服务网。其中，江孜站点为1956-2016年61年逐日气象资料；贡嘎及墨竹工卡站点为1991-2016年26年逐日气象资料。

1.2 计算参考作物蒸散量的6种模型

(1)FAO 56 Penman-Monteith(FAO 56 PM)。FAO 56 Penman-Monteith模型是基于水汽扩散理论和能量平衡为基础建立的并被FAO推荐为目前计算ET0的标准方法。该模型综合考虑了所有气象因子对ET0的影响且具有较完整的理论依据，常被用来评价其他ET0计算模型的精度，属综合法范畴[1]。国内学者的研究成果已证明了该方法在我国具有较高的普适性[4]。因此，本研究以FAO 56 PM模型计算的ET0值为标准，对本文中其他5种模型进行适用性评价。

(1)

式中：ET0为参考作物蒸散量，mm/d；Δ为饱和水汽压-温度曲线斜率，kPa/℃；Rn为太阳净辐射，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；γ为湿度计常数，kPa/℃；T为2 m高度处日平均气温，℃；es为温度为T时的实际水汽压，kPa；ea为温度为T时的饱和水汽压，kPa；U2为2 m高处的日平均风速,m/s。以下与此公式中的参数、符号相同者意义均相同。

(2)FAO 17 Penman(FAO 17 PM)。FAO 17 Penman模型是基于能量平衡法并引入干燥力的概念后得到的仅需普通气象资料可计算ET0的方法，属综合法范畴[12]。

(2)

式中：p0为海平面气压，hPa；p为本站地面气压，MPa；a1=0.26[13]；b1=0.14[13]。

(3)Hargreaves-Samani(HS)。Hargreaves-Samani模型是基于温差来反映辐射项的ET0计算法，该模型被证明是缺失辐射资料情况下的估算ET0的有效方法之一，属温度法范畴[14]。

ET0=∂(T+17.8)(Tmax-Tmin)0.5Ra

(3)

式中：∂为参数，取0.002 3；Tmax为2 m高度处日最高气温，℃；Tmin为2 m高度处日最低气温，℃；Ra为大气顶层辐射，MJ/(m2·d)，计算公式为[13]：

3.3.3 人类活动影响分析 人类通过实践活动，不断影响并改造着大气圈、水圈、岩石圈及生物圈.人类活动于遥感影像上最直接的体现即为地表覆被的变化.通过对土壤侵蚀与土地利用类型的研究，进一步探讨人类活动对土壤侵蚀的影响.基于Landsat影像，通过监督分类的方法，获取椒江流域各年份地表覆被情况椒江流域土壤侵蚀与地表覆被统计见表4(其他主要为居民地所产生土壤侵蚀的统计，微度侵蚀中包含水体统计).

Ra=37.6dr(wssinφsinδ+cosφcosδsinws)

(4)

dr=1+0.033 cos(0.017 2J)

(5)

ws=arccos (-tanφtanδ)

(6)

式中：dr为日地相对距离，无量纲；ws为日照时数角，rad；φ为地理纬度，rad；δ为太阳磁偏角，rad；J为日序数，例如1月1日为1，逐日累加。

(4)Makkink[15](Mak)模型，属辐射法范畴。

(7)

式中：Rs为太阳辐射，MJ/(m2·d)，计算公式为[11]：

(8)

(5)Priestley-Taylor(PT)。Priestley-Taylor模型是假定在湿润环境条件下，忽略了空气动力学项并引进参数而得出的简化算法，是Penman方程的简化式，属辐射法范畴[16]。

(9)

(6)Irmark-Allen。Imark-Allen(IA)模型是基于美国湿润地区资料得到的经验式，计算时需输入地理位置、气温、日照时数等参数。

ET0=0.489+0.289Rn+0.023T

(10)

1.3 数据分析方法

本研究依据典型性及全面性原则在各灌区范围内或附近选取一气象站点为代表站[17]，以FAO 56Penman-Monteith公式计算的ET0值为标准，对其他5种模型进行误差分析，其中误差统计变量包括平均绝对误差(MAE)、均方根误差(RMSE)和纳什效率系数(NSE)，并用Microsoft Office Excel 2010 计算统计变量并作图；对气象数据缺测值及异常值，本研究进行了合理插值，以期延长数据系列的长度。各统计变量计算公式为：

(11)

(12)

(13)

2 结果与分析

2.1 不同模型模拟的日ET0值比较

图1～3为HS、FAO 17 PM、PT、IA和Mak模型模拟的墨达、江北及满拉灌区的ET0日值变化。由图1～3可知，不同模型模拟的ET0日值在年际间呈先增后减的变化规律，且ET0最大值、最小值分别出现于6-7月、12-次年1月。HS、FAO 17 PM模型模拟的ET0最大值、最小值均大于FAO 56 PM模型的计算结果；较HS、FAO 17 PM模型，PT模型对ET0最小值的模拟结果吻合度较高；Mak、IA模型模拟的ET0最大值、最小值较其他模型的模拟值更接近于FAO 56 PM模型计算结果，但IA模型对ET0最小值的模拟结果存在高估问题。

图1～3直观地反映了各模型模拟值的变化趋势，但不足以定量评价其适用性。因此，本研究以FAO 56 PM计算值为标准，对其他5种模型进行相关性分析，结果见表2。由表2可知，FAO 56 PM计算值与其他5种模型模拟结果间线性关系极显著。各灌区中FAO 17 PM、HS、PT模型的斜率a介于1.58～3.06之间，决定系数R2介于0.83～0.91之间，说明这3种模型的模拟值偏大，存在高估现象，其高估程度依次排序为：PT模型>HS模型>FAO 17 PM模型；Mak、IA模型的斜率a介于0.82～0.98之间，决定系数R2介于0.84～0.89之间，说明这2种模型的模拟值较其他模型更准确。

表3为FAO 56 PM模型与5种ET0模型模拟结果间的误差统计结果。由表3可知，FAO 56 PM模型模拟的墨达、江北和满拉灌区多年平均ET0日值介于2.72～2.84 mm/d之间；HS、FAO 17 PM、PT、IA和Mak模型的模拟值介于2.91～7.75 mm/d之间，明显高于FAO 56 PM模拟结果。在各灌区中，FAO 17 PM模型的RMSE值介于1.83～2.03 mm/d之间，MAE值介于1.62～1.79 mm/d之间；HS模型的RMSE值介于4.80～5.30 mm/d之间，MAE值介于4.32～4.85 mm/d之间；Mak模型的RMSE值介于0.42～0.48 mm/d之间，MAE值介于0.35～0.39 mm/d之间；PT模型的RMSE值介于5.35～5.54 mm/d之间，MAE值介于4.69～4.91 mm/d之间；IA模型的RMSE值介于0.68～0.75 mm/d之间，MAE值介于0.62～0.68 mm/d之间。由各模型的MAE、RMSE值排序(PT模型>HS模型>FAO 17 PM模型>IA模型>Mak模型)可以看出，PT模型模拟的ET0日值距FAO 56 PM计算结果的离散度最大，计算精度最低；Mak模型的离散度最小，精度最高；其他模型的离散度及计算精度介于PT与Mak模型之间。分析NSE值发现，FAO 17 PM、HS、PT模型在3个灌区的NSE值均小于0，表明模型的计算可信度有待提高；Mak、IA模型的NSE值均大于0，表明模型的计算结果具有一定的可信度。其中，Mak模型的NSE均值(0.84)较IA(0.60)更接近于1，说明Mak模型的模拟质量、计算可信度更高，IA模型次之。

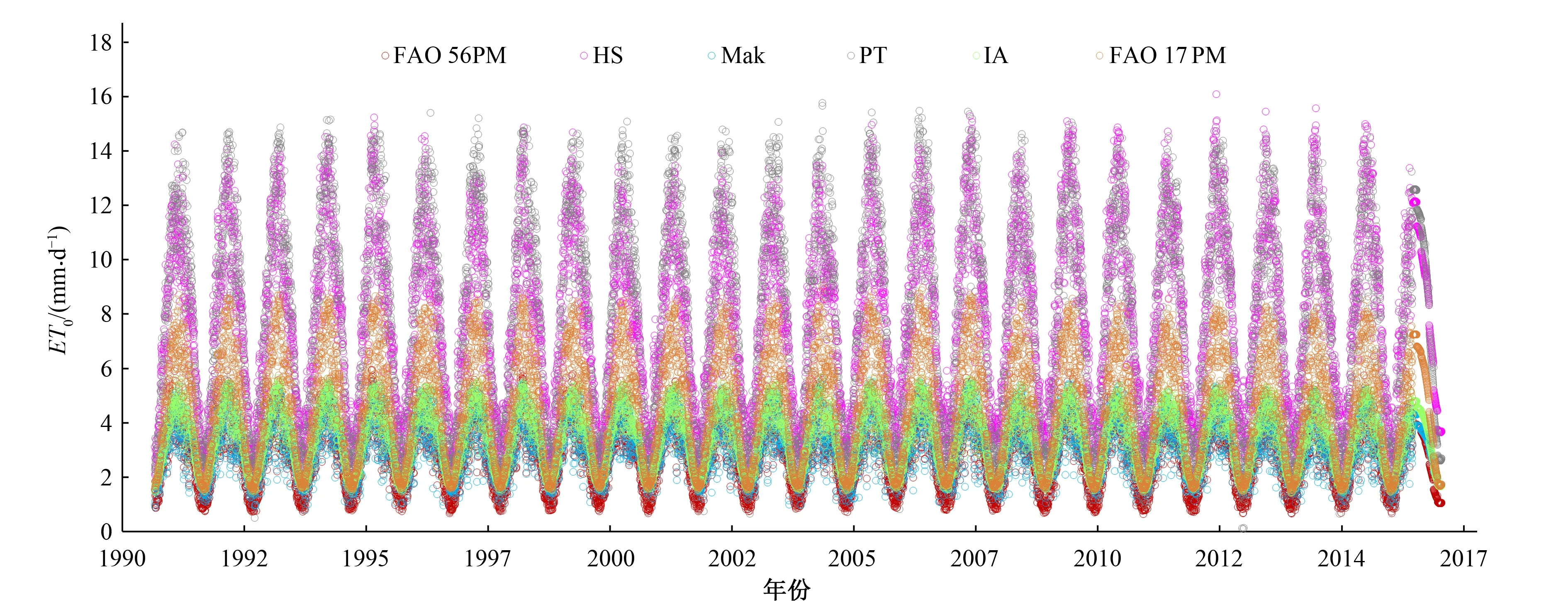
图1 江北灌区ET0日值变化

图2 墨达灌区ET0日值变化

图3 满拉灌区ET0日值变化

综上认为，各模型在模拟墨达、江北和满拉灌区ET0日值方面，其适用性存在明显差异。其中，Mak模型的模拟效果最优，适用性最好；IA模型次之；FAO 17 PM、HS和PT模型较差，且较FAO 56 PM模拟结果，ET0日值存在不同程度的高估问题。

表2 FAO 56 PM与其他5种模型模拟的ET0日值间的回归系数

注：表中“a”为相关分析拟合直线斜率；R2为确定性系数；“**”表示极显著相关(p<0.01)。

表3 FAO 56 PM与其他5种模型模拟的ET0日值间的误差分析

2.2 不同模型模拟的ET0年值比较

各ET0模型模拟的灌区ET0年值变化见图4～6。由图4～6可知，FAO 17 PM、HS、Mak、PT及IA模型模拟的江北、墨达和满拉灌区ET0年值普遍高于FAO 56 PM模拟结果。对比分析发现，Mak模型模拟值最接近于FAO 56 PM的模拟结果，IA模型次之，这与日尺度的模拟结果一致。从ET0年值变化趋势可以看出，FAO 17 PM、Mak、PT、IA模型模拟值的变化趋势与FAO 56 PM模型的基本一致，但HS模型在江北、墨达灌区的模拟情况却与之相反。此外，HS、PT模型模拟的ET0年值在年际间的浮动变化较其他模型大；FAO 17 PM和IA模型的变化较平稳，但Mak模型的浮动变化与FAO 56 PM模型的相近。

误差分析结果(表4)表明，江北、墨达和满拉灌区中PT模型的MAE值介于1 692.45～1 786.01 mm/a之间，RMSE值介于1 693.49～1 786.65 mm/a之间；HS模型的MAE值介于1 535.71～1 768.79 mm/a之间，RMSE值介于1 536.88～1 733.80 mm/a之间；FAO 17 PM模型的MAE值介于568.28～647.08 mm/a之间，RMSE值介于575.05～647.51 mm/a之间；IA模型的MAE值介于194.07～214.69 mm/a之间，RMSE值介于195.32～218.00 mm/a之间；Mak模型的MAE值介于76.19～80.90 mm/a之间，RMSE值介于81.08～83.53 mm/a之间。对比分析发现，PT模型的MAE、RMSE值最大；Mak模型的MAE、RMSE值最低，这表明PT模型的模拟精度最低，Mak模型的最高，其他模型模拟精度介于二者之间。由各灌区不同模型的NSE值可知，FAO 17 PM、HS、PT模型的NSE值介于-3571.76～-118.00之间，其结果远远小于0，表明该模型的模拟结果不可信；Mak模型的NSE值较其他模型更接近于0，表明该模型模拟结果接近于FAO 56 PM的模拟值，即总体模拟结果可信，但模拟过程的误差较大。

图4 江北灌区ET0年值变化

图5 墨达灌区ET0年值变化

图6 满拉灌区ET0年值变化

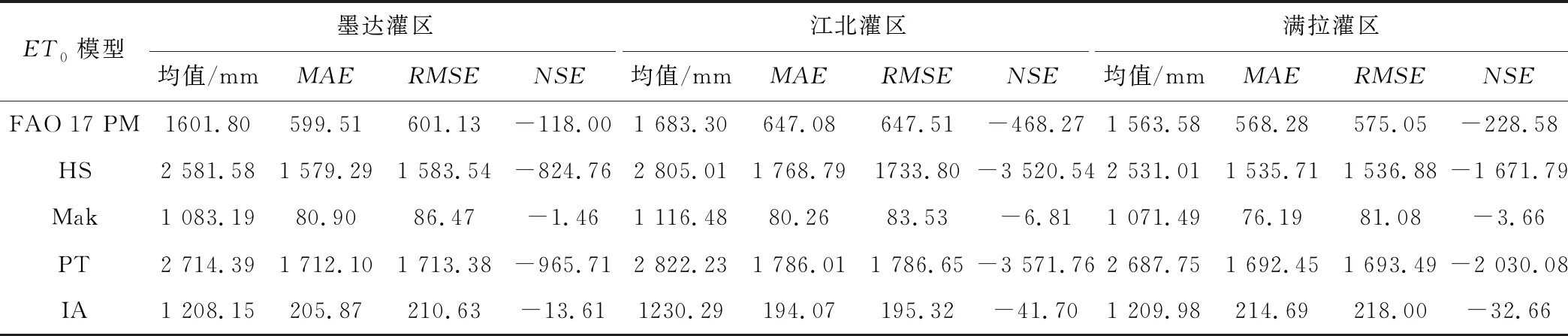
表4 FAO 56 PM与其他5种模型模拟的年ET0值间的误差分析

3 讨 论

国内外学者研究并提出了多种基于温度、辐射、风速及综合气象参数的ET0计算模型[18,19]，但起初因模型建立的需要，模型的结构中引进了不同的估算系数、空气动力学项及辐射项参数，致使多数模型在实际应用中受区域下垫面及气候变化的影响，导致其普适性变差。因此，在实际应用中需对ET0计算模型进行适用性评价，避免盲从引起作物需水量计算的精度降低。

本研究以FAO 56 PM模型模拟的西藏江北、墨达和满拉灌区的ET0值为标准，分别采用5种参考作物蒸散量模型模拟ET0变化，并从不同时间尺度进行了分析。日尺度上，Mak、IA、FAO 17 PM、HS和PT模型的模拟值变化趋势与FAO 56 PM模型的基本一致，在年际间呈先增后减的变化规律，且模拟值分别在6-7月、12月-次年1月出现峰值和谷值。但各模型的模拟效果存在明显差异，其中Mak模型的模拟质量及适用性最好，RMSE、MAE、NSE值分别为0.45 mm/d、0.37 mm/d、0.84；IA模型次之，RMSE、MAE、NSE分别为0.71 mm/d、0.65 mm/d、0.62；PT模型的最差，MAE值最大达4.91 mm/d，NSE值为-21.65，模拟结果的可信度低。年尺度上，各模型的模拟值较FAO 56 PM计算结果均存在高估现象，以PT模型最为突出。误差分析结果(表4)表明，PT模型的MAE、RMSE值最大，Mak模型的MAE、RMSE值最低，这说明PT模型模拟的ET0年值的精度最低，Mak模型的模拟精度最高。此外，年NSE值进一步也证实了PT模型的模拟结果不可信，而Mak模型结果总体可信，但在年尺度的模拟过程中Mak模型的误差较大。由徐冰等[8]在西藏当雄、那曲、改则等地研究认为的PT模型在日、年尺度上的模拟效果均最优的结论可知，同一种ET0计算模型在西藏高原的适用性存在区域差异，这与海拔、气象条件及区域下垫面的差异有关。

西藏高原平均海拔4 000 m以上，特殊的地域环境决定了西藏高原区气候具有低气温、强辐射的区域特征。因此，完全基于温度参数的HS模型难以反映出藏区高原实际强辐射条件下的ET0变化。此外，HS模型也未考虑空气动力学项影响[20]，这是引起该模型计算结果无论是在日尺度还是在年尺度中均较FAO 56 PM模型计算结果存在较大偏差的主要原因。而Mak、IA模型则是以辐射参数为基础的估算方法，在本研究中较其他3种模型在日尺度和年尺度上均表现出较好的适用性，且MAE、RMSE及NSE分析也证实了Mak、IA模型模拟结果的准确性及可靠性。然而，IA模型结构中由于仅考虑了平均温度的影响，未考虑水汽压差、净辐射、总辐射等关键气象因子的影响[21,22]，致使其模拟精度及可靠性较Mak模型低。PT模型的模拟结果较FAO 56 PM存在较大偏差，其主要原因与PT模型计算时运用了不同的修正参数计算的空气动力学项和未考虑相对湿度变化的影响有关[16]，即PT模型是假定在湿润条件下并忽略了空气动力学项影响后仅引进常数α=1.26进行代替而得出的简化方法，并未考虑不同区域特征对α值的影响[23]；已有的研究结果表明ET0与相对湿度间呈负相[24]，即当未考虑相对湿度对ET0的影响时，将引起PT模型计算结果偏大，这在本研究中已得到证实。虽然，FAO 17 PM模型与FAO 56 PM同属于综合法，也考虑了空气动力学项及辐射项的影响，但2种模型因采用了不同的空气动力学和辐射项计算公式，致使其结果间存在较大偏差。而造成FAO 17 PM模型日、年尺度模拟值均大于FAO 56 PM模型计算结果的主要原因与FAO 17 PM模型的结构中未考虑土壤热通量的影响[25]有关。然而，综合法因其模型结构中需估算的中间参数较多且计算过程繁杂，同时细节误差也可能会影响计算结果，使得目前关于综合法的评价研究仍存在不确定性[18]。

4 结 论

本文根据西藏高原江北、墨达和满拉灌区的长系列气象资料，以FAO 56 PM模型计算值为参照标准，对Mak、IA、FAO 17 PM、HS和PT模型进行分析验证后认为：

(1)Mak、IA、FAO 17 PM、HS和PT模型模拟的西藏高原江北、墨达和满拉灌区的日尺度ET0变化趋势与FAO 56 PM模型的一致，均在年际间呈先增后减的变化规律，且各模型模拟值分别在6-7月、12月-次年1月出现峰值和谷值。

(2)线性回归及误差分析表明，Mak、IA、FAO 17 PM、HS和PT模型在江北、墨达和满拉灌区的适用性存在明显差异。其中，Mak模型的日尺度模拟精度及可信度最高，MAE、RMSE、NSE值分别为0.37 mm/d、0.45 mm/d和0.84；IA模型次之，RMSE、MAE、NSE分别为0.71 mm/d、0.65 mm/d、0.62；PT模型最差，MAE值最大达4.91 mm/d且NSE值小于0，其模拟结果可信度低。年尺度中，各模型较FAO 56 PM均存在高估现象，以PT模型最为突出。但相对而言，PT模型模拟精度最低，模拟质量不可信；Mak模型精度最高，模拟质量总体可信，但模拟过程误差较大。

(3)Mak模型结构简单，所需气象资料少，且模拟结果无论在日尺度还是年尺度中均最接近于FAO 56 PM模型的模拟结果。综合评定，可以考虑将Mak模型作为代替FAO 56 PM模型来计算西藏高原灌区气象数据缺测下ET0值。