受限洪泛策略的内容中心网络路由算法

吴文刚 王庆生

1(山西经济管理干部学院电子信息工程系 山西 太原 030024)

2(太原理工大学信息与计算机学院 山西 太原 030024)

0 引 言

随着网络日益扁平化和网络连接资源的日趋丰富，网络拓扑结构也变得愈加复杂，获取网络资源所需要的网络跳数也愈来愈少[1]。面对网络扁平化的趋势，TCP/IP网络提出了一系列的新型网络协议[2-3]，例如：P2P协议提供对等网络进行去中心化的数据传输以进行直接的共享资源与服务;CDN协议则通过DNS重定向技术在网络中部署节点服务器以便于域内获取网络数据与资源等。然而，内容中心网络(Content-Centric Network,CCN)作为一种未来网络体系架构，仍然采用基于最优路径的方式获取数据[4]。如果以内容提供商作为根节点，以请求该内容提供商数据的用户为叶节点，那么网络中所有针对该内容提供商的数据请求路径将构成一颗请求树。显然，这样的树状数据请求结构无法更好地适应日益突出的扁平化网络结构，如何探索网络中其他位置的缓存内容成为了提升CCN转发效率最重要的挑战[5]。

为了解决上述挑战，本文采用探索的方法，尽可能地获取网络最近副本的位置，这需要在网络转发的策略上进行改变和创新。当前的CCN网络层中，转发一个兴趣包时，主要有两种转发策略可以选用：最优路径算法和多路径转发。

最优路径算法类似于IP网络中的最长掩码匹配，即根据路由表提供的路由信息自适应地选择最优的转发路径。国内外一些研究结合了CCN网络的特性，针对最优路径算法提出了一系列自适应的、有状态的转发策略，使CCN转发层相比于IP网络的转发层更加智能[6-9]。然而，最优路径算法目前仍然无法支持最近副本路由，这使得对于热门数据，除非最优转发路径的缓存中存在相应的副本，否则大量的网络缓存对于用户来说全部是透明的，这极大程度地限制了网络的性能[10-11]。

相比之下，多路径转发则可以尽可能地返回最近的内容副本。作为多路径转发最极端的情况，洪泛算法釆用广播的方式，虽然可以最大程度地利用网络资源，返回最近的内容副本，但是由于多路径路由带来了较大的开销，在实际网络中并不能得到真正应用。

由此可见，多路径路由可以从本质上解决CCN网络无法支持最近副本路由的问题，但是采用多路径路由的最大挑战是：如何在尽可能保证性能的前提下，最大程度地降低多路径路由带来的开销。为了解决这一问题，本文基于多路径路由中最简单的洪泛算法，提出了一种受限洪泛策略来极大地减小原始的洪泛算法的开销。使用洪泛算法有以下几个优点[12-14]：

1) 降低复杂性。洪泛算法可以极大地降低协议复杂性并简化协议设计。特别地，文献[11]中指出，洪泛算法在某些不稳定的网络环境中最适用。

2) 发现邻居内容。在CCN中，除了路径缓存外，用户请求同样需要处理强大的空间位置[14]。换言之，就是说在某一路由器周围的路由器中很大可能地缓存了用户请求的某些热门数据。如果对于用户，这些邻居中缓存的数据是透明的，那么洪泛算法是最适合发现邻居节点缓存内容的算法。

3) 减小路由状态。相对于最优路径算法，洪泛算法在基于路由的内容发现机制方面，所需要维护的网络状态相对比较少。

4) 降低通信成本。在CCN中，利用相近邻居互相交换数据，相比于使用回程的方法，开销相对比较低。

本文针对CCN网络转发层存在的问题，结合洪泛算法和最优路径算法，通过控制洪泛区域降低开销的方法，提出了新型的RFS算法来解决网络无法获取邻居节点缓存副本的问题。提出的RFS*算法在开销几乎不变的条件下，大幅降低分发数据获取的网络时延。

1 RFS算法与理论分析

1.1 RFS算法

1.1.1参数定义

在描述RFS算法与理论分析之前，先定义一些算法中需要用到的参数。

定义1域内洪泛算法。相对于传统的粗暴型洪泛(不受任何限制的洪泛算法)，将洪泛范围缩小至某一可控区域内的洪泛算法称为域内洪泛算法。

定义2洪泛生存时间FTTL(Flooding TTL)、最大洪泛生存时间mFTTL(Maximal FTTL)、洪泛数量NF(Number of Flooding)。在域内洪泛算法中，FTTL代表洪泛包当前的生存时间；mFTTL代表FTTL上限；NF代表当一个路由器收到某一兴趣包时，洪泛至上游路由器的最大数量。

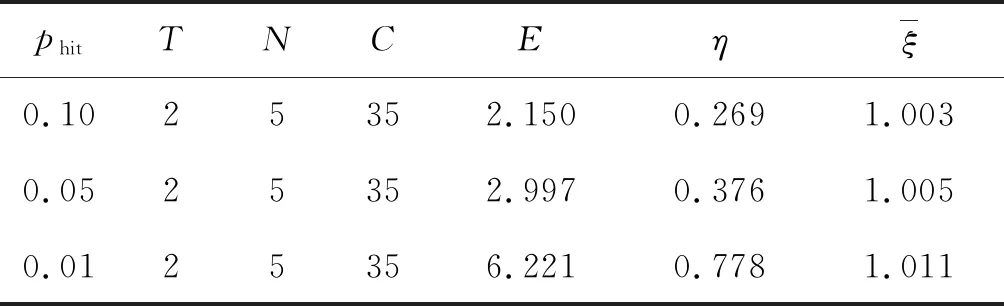
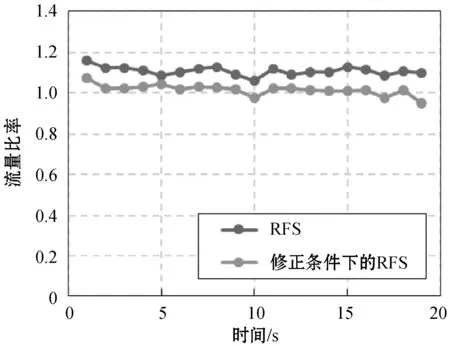
在域内洪泛算法中，FTTL(mFTTL)和NF分别从洪泛的深度和广度两个角度来控制洪泛算法的区域。假如针对某一兴趣包采用基于域内洪泛算法的转发策略，且mFTTL=3、NF=2，则在当路由器收到该兴趣包时，首先检查当前的洪泛生存时间是否已经达到最大的洪泛深度，即比较FTTL与mFTTL。如果FTTL

定义3R-路由器。对于某一给定的兴趣包，沿最优转发路径的第一台上游路由器(即与用户最近的路由器)定义为R-路由器。

定义4F-深度。对于某一给定的兴趣包和当前收到该兴趣包的路由器，从R-路由器开始，沿着该兴趣包到达该路由器的转发路径所需要的跳数定义为F-深度。特别地，R-路由器的F-深度定义为0。

定义5B-路径、F-路径、B-路由器、F-路由器。对于某一给定的兴趣包：1) 如果根据路由表，沿着最佳路径转发的路线，从R-路由器开始直至内容提供者，这段路径定义为B-路径，其路径上的路由器定义为B-路由器；2) 如果采用域内洪泛算法，从R-路由器开始直至F-深度为mFTTL的路由器，这段路径定义为F-路径，其路径上的路由器定义为F-路由器。

值得注意的是，对于某一给定的兴趣包，其B-路径至多只有一条，而F-路径可以有多条。另外，对于某些路由器，有可能既是B-路由器，也是F-路由器。

定义6k-F-子路径。对于某一给定的兴趣包，在其某一条F-路径上，从F-深度为k-1的F-路由器到F-深度为k的F-路由器的这条路径定义为k-F-子路径。

如图1所示，对于某一兴趣包釆用域内洪泛算法，并定义mFTTL=3、NF=1。可以看到，图中共有1条B-路径、3条F-路径、3台B-路由器和5台F-路由器。

图1 RFS相关定义示意图

1.1.2算法描述

RFS算法伪代码如算法1所示。

算法1RFS算法

RFS(Interestinterest,intf_depth)

//如果为F-路由器

ifinterest.lable==F

interest.f_ttl++;

ifinterest.f_ttl

//随机选择NF台下一跳路由器进行洪泛

RamdomFlooding(interest,NF);

else

Drop(inte);

endif

//如果为B-路由器

else

ifR-router

interest.f_ttl=0;

else

interest.f_ttl++;

endif

//首先沿B-路径转发

BestRoute(interest);

ifinterest.f_ttl

//增加F标签并进行洪泛

f_interest=interest.getCopy();

f_interest.lable=F;

RamdomFlooding(f_interest,NF);

endif

endif

基于上文的若干定义，对于某一给定的兴趣包，RFS算法描述如下：

初始化：

将兴趣包的FTTL初始化为0。

算法开始：

1) 如果当前路由器为R-路由器或B-路由器，则:

① 如果当前路由器为R-路由器，则FTTL=0，否则FTTL增加1。

② 根据路由表，沿B-路径转发该兴趣包。

③ 比较当前兴趣包的FTTL与mFTTL的大小。如果FTTL

2) 如果当前路由器为F-路由器(即检测到兴趣包带有标签F)，则:

①FTTL增加1。

② 比较当前兴趣包的FTTL与mFTTL的大小。如果FTTL

算法结束：用户收到兴趣包对应的数据包。

1.2 理论分析

本节将从理论上分析RFS的性能和开销。在进行理论分析之前，先给出一些参数定义和符号定义。

定义7洪泛覆盖。对于某一给定的兴趣包，釆用RFS算法后，其洪泛包的总数定义为洪泛覆盖。

显然，洪泛覆盖代表使用RFS算法产生的额外开销，即网络额外产生的兴趣包数量。

定义8路径长度比率。对于某一给定的兴趣包，路径长度比率η定义为:

(1)

定义9流量比率。对于某一给定的兴趣包，流量比率ξ定义为：

(2)

基于上述定义，先给出几个基本的定理。

定理1在RFS算法中，令N代表洪泛数量NF，T代表最大洪泛生存时间mFTTL,C代表洪泛覆盖,则C满足：

(3)

证明：首先考虑一个F-深度为m(m

(4)

考虑到在B-路径上至多有T个节点可以触发转发洪泛包的机制来产生上述的N叉树，这些节点的F-深度0≤m

(5)

证毕。

在进一步理论分析前，令pi代表某一缓存i的缓存命中概率(Probability of cache-hit)。因此，根据定理1，在RFS算法中，所有的F-路由器(共C台)的缓存命中概率分别表示为p1,p2，…，pC。为了简化分析过程，本节对所有缓存命中概率pi做出以下假设。

假设1假设网络中所有的缓存命中概率相等。

p1=p2=…=pC=phit

(6)

定理2在RFS算法中，令T代表最大洪泛生存时间mFTTL，L代表内容提供商的F-深度，则路径长度比率η满足：

(7)

证明：对于某一给定兴趣包，在RFS算法中，域内洪泛的兴趣包均没有命中缓存的概率P为:

P=(1-p1)(1-p2)…(1-pC)=(1-phit)C

(8)

因此，在域内洪泛中，至少有一个兴趣包命中缓存的概率为1-P。注意到F-路由器的F-深度最大值为T，因此可以算出使用PRS算法匹配数据成功的F-深度的期望值EPRS。

EPRS≈LP+T(1-P)=T+(L-Y)P

(9)

因此，根据定义8，路径长度比率η为：

(10)

理想情况下，C→∞，则(1-phit)C→0，因此可以得到EPRS和η下限值：

(11)

(12)

证毕。

根据定理2可以得出结论：在理想情况下，使用RFS算法获取数据包所需要的跳数平均最少需要最优路径算法获取数据包所需要的跳数的T/L。显然，T越小，η的下限T/L越小，但是在实际情况下，T越小通常也意味着洪泛覆盖C越小，这样EPRS和η都很难逼近理论下界。因此，如何最优化T值需要结合式(3)和式(10)进行仿真分析。

假设2假设网络中所有兴趣包大小Mint相等，所有数据包大小Mdata相等，且满足：

Mdata=50Mint

(13)

定理3在RFS算法中，令T代表最大洪泛生存时间mFTTL，L代表内容提供商的F-深度，phit代表平均缓存命中概率，C代表洪泛覆盖，则流量比率ξ满足以下公式：

(14)

证明：针对某一特定兴趣包产生网络的总流量，在未使用RFS时，总流量为L·Mdata,使用RFS时，除了产生这部分流量以外，还需要额外产生流量。

T·(1-phit)C·Mdata+C·Mint

(15)

因此，根据定义9，网络的流量比率ξ为:

(16)

整理后即得式(14)。

证毕。

结合定理2和定理3，可以通过仿真计算找到最优化的(T,N)数据对，使得η和ξ的值尽可能小。假设内容提供商的F-深度L=8，命中率phit分别为0.1、0.05、0.01。通过计算，得到了若干有意义的(T,N)数据对，如表1所示。可以看出，考虑所有不同的缓存命中率的情况下，当(T,N)=(2,5)时，在得到接近最优性能的同时，开销也控制在相对比较低的水平。从分析可以发现，缓存命中率phit对性能和开销的影响均比较大，因此采用什么样的缓存策略也将较大地影响算法的最终效果。

表1 RFS算法(T,N)数据对

1.3 RFS算法触发条件

1.3.1触发条件

值得注意的是，针对某一兴趣包，虽然网络总流量增加并不多，但网络的转发压力陡增。以命中率phit=0.01为例，本节选择最优的方案(T,N)=(2,5)，尽管此时网络的总流量比率ξ=1.263并不是特别高，即在可接受范围内，但是对于某一兴趣包，由于RFS算法引发的网络中额外的兴趣包数量(即洪泛覆盖)为C=35，而不使用RFS算法时网络中该兴趣包数量为L=8，因此，网络转发压力变为原来的437.5%。

显然，为了提高网络性能，额外增加这样大的网络开销是不能接受的，因此何种情况才能触发RFS算法是需要考虑的问题。值得注意的是，由于网络协议限制，网络传输的数据包大小有上限(例如4 096 KB)，因此，当用户请求相对较大的数据时，需要发送多个兴趣包才能将全部数据取回。这样，用户请求较大的数据所发出的兴趣包可以分为以下两种：

1) 新兴趣包：当用户请求某一数据时，第一个发出的兴趣包定义为新兴趣包。通常来说，新兴趣包的名字中的序列编号为0。

2) 后续兴趣包：当用户请求某一数据且已经发出了第一个兴趣包，后续再发出的请求该数据剩余数据块的兴趣包定义为后续兴趣包。

由于RFS算法的根本目的是探索网络数据副本的缓存位置，因此针对某一兴趣包，采用RFS算法有效的条件包括以下两点：

1) 兴趣包所请求的数据在网络非转发路径的位置中有可能存在被缓存的副本。

2) 兴趣包所请求的数据尚未使用过RFS算法进行转发，否则只需要继续沿着上次执行RFS算法找到的位置获取数据即可。

由此，得出触发RFS算法的两个必要条件：

1) 兴趣包为新兴趣包。

2) 所请求的数据为分发数据(即不是端到端数据)。

算法触发条件的伪代码如算法2所示。基于该触发条件的RFS算法称为修正条件下的RFS算法——RFS*算法。

算法2RFS触发算法

RFSTrig(Interestinterest,intf_depth)

//如果不是新兴趣包，采用BestRoute

ifinterest.name.seq_number!=0

BestRoute(interest);

Return；

endif

//如果不是分发数据

ifinterest.type==END_TO_END

BestRoute(interest);

Return；

endif

//如果满足触发条件

RFS(interest,f_depth);

1.3.2理论分析

考虑RFS触发条件，对理论分析结果进行一定修正。显然，修正的结果并不影响η值，因此仅需要考虑ξ值。

假设3假设网络中分发数据平均为最大传输数据块的K倍。

(17)

根据定理4，当K=25，取最优数据对(T,N)=(2,5)时，网络参数如表2所示。可以看到，在修正条件下，网络性能(获取数据的平均跳数)提升明显的同时，网络的额外开销(网络总流量)几乎控制在可以忽略不计的范围内(1%)。

表2 RFS*算法相应的最优数据对(T,N)

2 仿真实验

本节通过仿真软件ndnSIM来对RFS算法和RFS*算法进行实验验证。最新版本的ndnSIM整合了CCN-cxx库(CCN C++ library with experimental extensions)和CCN转发进程NFD(CCN Forwarding Daemon)，以确保实验采用模拟环境的实际代码。

2.1 实验设置

实验环境：运行ndnSIM的计算机的配置包括中央处理器采用英特尔酷睿四核i7-4790处理器，内存大小为8 GB。通过修改ndnSIM的底层代码，使ndnSIM支持RFS算法所需要的所有参数。

网络拓扑：所有仿真实验中，并未使用复杂的真实网络拓扑，而是采用了15×15的网格拓扑结构。这225个节点中，四角的节点(0,0)、(0,14)、(14,0)和(14,14)作为网络的内容提供商，而其他221各节点中，随机设置30%的节点作为用户，70%的节点作为网络路由器。其他网络拓扑的参数均设为理想状态下的参数，确保网络任何环节(如转发能力、带宽等)均无瓶颈。

参数设定：取最优数据对(T,N)=(2,5)，内容提供商的F-深度L=8，缓存命中率phit=0.1，网络中分发数据平均大小与最大传输数据块的比值K=25。用户采用发送兴趣包的方法：当用户发出一个兴趣包后进入等待状态，在网络返回相应的数据包之前，用户不再继续发送兴趣包；当网络返回相应的数据包后，用户立即发送下一个兴趣包。

2.2 实验结果

2.2.1性能对比

首先来考察使用最优路径算法和RFS算法(包括RFS*算法)的性能对比。在前面的理论分析中已说明修正条件并不会影响RFS算法的性能，因此本节并不额外对比RFS*算法的结果。

定义兴趣包满足数NSI(Number of Satisfied Interest)代表用户每秒钟发送出去的兴趣包数量。显然，NSI越高，算法的性能越好。利用NSI可以计算得到实验条件下的路径长度比率ηex：

(18)

首先，通过实验得到不同算法下NSI随时间变化的曲线，如图2所示。可以看到，在使用RFS算法后，NSI的值有了明显的提升，基本稳定在1 300左右的范围内；而仅仅使用Best-route算法，NSI值基本在400左右。基于这两条NSI曲线，得到了路径长度比率ηex随时间变化的曲线，如图3所示。可以看到，ηex基本保持在0.30左右，平均值为0.29，基本与理论值0.269保持吻合。由式(18)可知，1-ηex=1-0.29=0.71表示使用RFS算法带来的性能平均提升比率。

图2 兴趣包满足数NSI对比

图3 路径长度比率ηex

实验结果表明：在当前实验条件下，使用RFS算法后网络性能平均提升(网络时延降低)了71%。

2.2.2开销对比

本节考察最优路径算法、RFS算法和RFS*算法三者的开销对比。通过定义平均单兴趣包网络流量(Average Traffic per satisfied Interest packet,AT)来代表每一被满足的兴趣包所需占用的网络总流量。利用AT可以计算得到实验条件下的网络流量比率ξex：

(19)

首先通过实验考察三种算法的值随时间变化的曲线。如图4所示，使用最优路径算法后平均单兴趣包网络流量AT在区间[1.032,1.066]内，均值为1.044，均方差为0.009;使用RFS算法后AT在区间[1.133,1.249]内，均值为1.156，均方差为0.029；而使用RFS*算法AT在区间[0.992,1.141]内，均值为1.059，均方差为0.030。可见，使用了RFS算法和RFS*算法后，由于获取数据位置的不确定性，AT变化相对于最优路径算法的AT变化要大得多。

图4 平均单兴趣包网络流量AT对比

基于AT随时间变化的曲线得到如图5所示的流量比率ξ随时间变化的曲线。可以看到，使用RFS算法流量比率ξ在区间[1.061,1.162]内，均值为1.107(理论值为1.094)；而使用RFS*算法流量比率ξ在区间[0.949,1.070]内，均值为1.006(理论值为1.003)。实验结果与理论结果基本吻合。

图5 流量比率ξ对比

根据实验结果，由图4中前20秒AT的均值数据可以算出使用RFS和RFS*算法带来的网络开销的增量。可得以下结论：在当前实验条件下，使用RFS算法后网络开销(网络总流量)平均增加了10.7%；而使用RFS*算法后网络开销(网络总流量)平均仅增加了0.6%。

3 结 语

本文提出了新型的RFS算法，较好地解决了CCN网络转发层节点缓存副本无法获取的问题。提出的RFS*算法能够在几乎不带来额外开销的条件下，大幅提升网络性能。结合理论分析和实验验证，证明了RFS*算法对解决目前CCN网络转发层问题的有效性。下一步，将把RFS*算法应用于复杂的CCN网络中并对其进行验证。